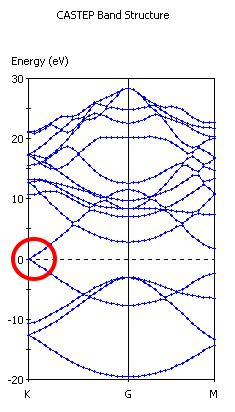
二、石墨烯 (graphene) ,也就只有單一層碳原子層的石墨 (graphite) 材料,其能帶結構有一個有名的零能隙的交叉點費米面,其周圍是近乎直線的能帶,叫做迪拉克 (Dirac) 點,請重現之。
問題分析:建立模型並進行能帶結構計算,從圖上找出符合特徵之處。(在布里淵區中所謂的 K 的高對稱點處)
操作要點:利用石墨結構,切除不要的碳平面層,就可以留下只剩一層,所有 k 取樣,及 k 路徑,用 n × m × 1 (因為沿著 C 軸方向沒週期性)就可以了。
參考畫面:
2014 計算材料 期中考
(每題二十分,請聽從助教指示作答)
(原子分子)
一、驗證 CO2 為線性分子而 H2O 為彎曲分子。
問題分析:為了要知道自然界是否偏好讓 O - C - O 形成一直線而 H - O - H 保持有角度,使用 CASTEP 進行 Geometry Optimization 來幫我們預測 "最低總能量" 的分子構形。
操作要點:我們用 Atom Skecher 分別建構 O-C-O 與 H-O-H 兩個分子,並放入夠大(足以週期隔開)的超晶胞中, 用 CASTEP 進行 Geometry Optimization 的 Task。我們將會見到,CO2 的最低總能結構是 O - C - O 呈一直線,而 H2O 則形成一小於 180 度的鍵角。
小技巧:把 CO2 畫成 O=C=O 而非 O-C-O,就能在按 Clean 鈕下形成
參考畫面:
(能帶結構)
二、石墨烯 (graphene) ,也就只有單一層碳原子層的石墨 (graphite) 材料,其能帶結構有一個有名的零能隙的交叉點費米面,其周圍是近乎直線的能帶,叫做迪拉克 (Dirac) 點,請重現之。
問題分析:建立模型並進行能帶結構計算,從圖上找出符合特徵之處。(在布里淵區中所謂的 K 的高對稱點處)
操作要點:利用石墨結構,切除不要的碳平面層,就可以留下只剩一層,所有 k 取樣,及 k 路徑,用 n × m × 1 (因為沿著 C 軸方向沒週期性)就可以了。
參考畫面:

(投影態密度)
三、石英為寬能隙的晶體,其能隙的兩側,各是以氧為主抑或是以矽為主,請以原子選擇的投影態密度呈現出來。
問題分析:石英 (Quartz) 是 SiO2, Si 的投影態密度與 O 的投影態密度將會不同,能隙兩側的量子態對材料光學性質貢獻較大,可用 投影態密度來分析看那個元素比較重要。
操作要點:作 Task = Energy 的計算,Properties 選 DOS 並勾 PDOS。算完後 作在選定原子下的 PDOS 作圖,矽一張,氧一張,並列比較
參考畫面:(左:氧;右:矽)
(彈性係數張量)
四、鑽石在摩氏 (Mohs) 硬度表上是 10 ,剛玉(摻微量金屬則成藍寶石)是 9,石英是 7,而螢石 則是 4,試比較鑽石與螢 的彈性係數張量。
問題分析:CASTEP 可直接進行 彈性係數張量的計算,越不易變形(硬)的理想晶體材料,其對應張量的彈性係數值越大。(真實材料中常有缺陷,會進一步使材料弱化,故問題更加複雜,就不全由彈性係數張量唯一決定。)
操作要點:鑽石 (diamond, C) 及螢石 (fluroite, CaF2) 的模型都在 MS 找得到,載入後設 Task = Elastic Constants 即可。
參考畫面:diamond (left) ; fluorite (right)

(磁性)
五、比較金屬 鐵 與 鎳 的自發磁化率 (磁矩) 大小。
問題分析:進行 Spin-polarized 計算就可獲得材料磁矩(自發磁化率)的預測。
注意提醒:多數有操作的同學,都忘了設定自旋初始值,算出磁矩為零而不覺有異。
操作要點:用 Import 功能載入模型,在 CASTEP Calculation 選單中勾選 Spin-polarization(Task = Energy 即可,因為晶胞結構參數已是含理值,不必再最佳化。算完後,找 輸出文件 *.castep 中描述 Integrated Spin Density 的地方,即是自發磁化率 (磁矩) 。
參考畫面:
Fe
Ni