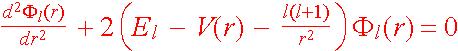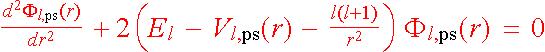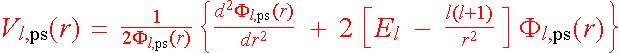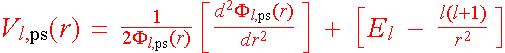密度泛函理論的方法與應用

密度泛函理論的方法與應用— CASTEP 計算

李明憲

淡江大學物理系

（未經作者同意不得轉載）

使用電腦模擬來進行材料設計

優點：（一）不受實驗條件的限制、（二）簡化研究的變因

缺點：必須使用足夠精確的物理定律

因此，目前電腦模擬的材料設計走向兩個趨勢：

（一）採取微觀尺度（因為物質由原子構成）、

（二）使用量子力學（才能正確描述電子行為以及由其所決定的機械、傳輸、光學、磁學等性質）

也就是說，原子之間的作用力以及材料所表現的物性，我們都希望能（不借助實驗結果）透過第一原理方法來達到。

密度泛函理論 與 單一粒子薛丁格方程式

一個穩定態（與時間無關）的單一粒子薛丁格方程式可表示為一個本徵值問題（暫略動能項的 h/2m），

H Y(r) = E Y(r)

[-▽² + V] Y(r) = E Y(r)

多體量子系統（如雙電子的薛丁格方程式）：

〔-▽₁² - ▽₂² + V(r₁, r₂)〕Y(r₁, r₂) = E Y(r₁, r₂)

在普遍的狀況下，V(r₁, r₂) 裏的 r₁, r₂是無法分離變數的，因此，即便簡單如雙電子的薛丁格方程式就己經沒有解析解了。而任何的計算材料的量子力學問題，都需要處理大量數目的電子。

密度泛函理論（Density Functional Theory：DFT）

量子力學告訴我們只要知道總波函數便可以決定系統的總能量

E[Y(r₁, r₂, r₃, ..., r_N)]

而 Hohenberg 及 Kohn 則證明了多體系統基態的兩個重要性質，構成所謂的 Hohenberg-Kohn 定理。它有兩個主要陳述，如下：

首先（陳述一），基態的總能可以寫成是電荷密度的泛函，也就是說，存在

E_G.S.[Y(r₁, r₂, r₃, ..., r_N)] → E_G.S.[r(r)]

這樣的對應關係。如此當然大大地簡化了求基態總能問題的自由度。

其次（陳述二），若將不是基態的電荷密度 r(r) 代入，一定會導致 E_G.S.[r(r)] ≧ E_G.S.[r_G.S.(r)] ，也就是說，該總能的電荷密度泛函 E_G.S.[r(r)] 滿足變分學原理。

利用上述性質，我們會想利用各種方法猜測 r(r)並代入 E_G.S.[r(r)] 求值，只要一直試到產生最低的能量，則該能量保證是基態的總能，且該電荷分佈保證是基態的電荷密度分佈。

在此要提醒大家，即使只是獲得基態，都已經足以預測很多性質了。例如，分子的鍵長，振動頻率，固體的晶胞邊長、彈性係數張量，甚至是化學鍵的斷裂或是生成，對電子而言都是基態的性質。因此，能預測系統的基態是非常有用的。

天下沒有白吃的午餐，密度泛函理論（或說 H-K 理論）只證明了 E_G.S.[r(r)] 存在，卻並未給出明確的形式或公式。我們因此只能寫下 E_G.S.[r(r)] 的近似，在將之分開成動能與位能兩個部分 E_G.S.[r(r)] = T_G.S.[r(r)] + U_G.S.[r(r)] 的情況下，其中由總電荷密度 r(r) 要得到位能 U_G.S.[r(r)] 比較容易，庫倫定律告許我們一個電荷分佈在空間中會建立怎麼樣的靜電位勢；然而同樣給定電荷分佈在空間間的函數，卻沒有什麼物理定律能精確告許我們基態的總動能 T_G.S.[r(r)] 。其實，物理學家在更早就已經試圖近似這一項，像湯瑪士—費米模型，其動能泛函 T[r] 使用自由電子氣的 k_F = (2/3) r^(1/3) ，再透過 k_F²來獲得一個粗糙的動能值。如此，總算是有一個明確的泛函可以把 r(r) 代進去求值。然而，它對材料物性的預測上並不理想。

Kohn-Sham 方法

（I：動能泛函與 Kohn-Sham 軌域）

一個多電子系統的基態總能泛函，原可以看成由以下三項泛函所構成：

E[r] = T_m[r] + E_ee[r] + E_ext[r]

Kohn 與 Sham 針對 T_m[r] 與 E_ee[r] 裏，物理學家己經知道有公式可描述的效應部分，抽離出了各粒子在獨自運動時的總動能 T_s[r] ，以及古典靜電分佈的庫倫位能 E_H[r] ，至於 T_m[r] 與 E_ee[r] 剩下的部分，則合併在一起稱為交換相干能 E_xc[r] 。

E[r] = T_s[r] + E_xc[r] + E_H[r] + E_ext[r]

如此一來，除了 E_xc[r] 之外，各泛函項就都有明確的公式可用了，其中 T_s[r] 的部分是

T_s[r] = 1/2 S_i∫Y_i^*(r) ▽²Y_i(r) d³r

其中

r(r) = S_i |Y_i(r)|²

並必須滿足歸一化條件

N = ∫r(r) dr = S_i∫Y_i^*(r) Y_i(r) d³r

注意這裏所寫出的 Y_i(r) 是單獨粒子的波函數，不是先前所定義的系統總波函數 Y(r₁, r₂, r₃, ..., r_N)，這些 Y_i(r) 又被稱作是 Kohn-Sham 軌域。H-K 定理放棄使用總波函數作自變數來使總能泛函簡化，但 K-S 方法為了求得較精確的動能又引入單粒子波函數於動能泛函中（畢竟用費米動量來近似動能誤差太大了），可說是一種以退為進的策略。

（II：交換相干能的局域密度近似）

另外，古典靜電位能 E_H[r] 的部分則是：

E_H[r] = ∫r(r') r(r) / |r' - r| d³r' d³r = ∫V_H(r) r(r) d³r

其中 V_H(r) = ∫r(r') / |r' - r| d³r' ，稱作 Hatree energy，是我們熟悉的靜電庫倫位勢。最簡單的則是外加位勢影響下的位能，其電荷密度的泛函可寫為

E_ext[r] = ∫V_ext(r) r(r) d³r

最後，即便不知道公式的情況下，我們一樣可以定義類似位勢的 e_xc[r(r)]（exchange-correlation energy per particle），如下：

E_xc[r] ≡ ∫e_xc[r(r)] r(r) d³r

在此 e_xc[r(r)] 仍是未知的，Kohn-Sham 方法裏的第二大重點，就是針對交換相干效應加以近似，

e_xc[ r(r) ] 〈未知〉～ e_xc^LDA( r(r) ) 〈近似〉

從泛函（函數的函數）近似成普通的函數

這相當於在講，原本需要知道整個 r(r) 函數分佈才知道空間中各點的 e_xc 大小，現在近似成只要給定位置 r0，代入 r(r) 得到該位置的 r0，就可以得到該位置的 e_xc^LDA 值。也就是說， e_xc 大小只跟那個位置的電荷密度大小有關，因此被叫作是局域密度近似（Local Density Approximation），簡稱 LDA。

大家可能會想到，既然 e_xc[ r(r) ] 是未知，那 e_xc^LDA( r(r) ) 一樣也是未知，此一問題的解決，是透過（以量子蒙地卡羅方法）計算各種不同密度 r 之下的均勻電子氣體的基態總能，即前述之 E[r(r)] （均勻電子氣體的基態電荷分佈也是均勻的，故 r 是常數函數）。得 E[r] 之後，減去可由密度求得之T_s[r] 、E_H[r] 、及 E_ext[r] ，剩下的即是 E_xc[r]。如此，不同常數 r 值所對應之 E_xc[r] 於是建立，好像是查表的動作，實用上則是擬合成一個參數式。這樣一來，總能泛函的每一項就都有明確的公式，我們也就可以針對不同 V_ext(r) 來猜 r(r) 求極小（基態）了。

（III：泛函微分求根及 Kohn-Sham 方程式）

現在，我們要問什麼樣的 r(r)（也就是說 {Y_i(r), i=1,2,...,N}）會使 E[r(r)] 最小（則 r(r) 就是基態的電荷分佈，且 E[r(r)] 就會是基態能量）。隨便亂猜不見得能得到最小，地毯式搜索也難保沒有遺珠之憾。回想在數學上想知道什麼樣的 x 值會讓函數 f(x) 最小時，最方便的方法就是體認到函數在其極值時其斜率為零（當然我們談的必須是平滑函數）。我們會將其一階導數 f'(x) 令為零來求解 x。

在此我們要針對總能泛函找極小，用的也是令斜率為零求解的策略，只不過泛函求導數比一般函數求導數稍微複雜一點，其實基本的原理是一樣的。泛函微分的公式及證明可見於一般泛函微積分或是物理數學中的變分學章節，在此我們會用到的形式恰好是最簡單的形式，可同“去掉積分，函數少一個”口訣來套用。

針對 E[r(r)] 中的各項，對 Y_i^*(r) 變分的結果，如下：（Y_i(r) 是複數值函數，相當於 a(r) + b(r) i ，有兩個自由度，因此也可以方便地把 Y_i^*(r) 與Y_i(r) 看成是兩個獨立函數）

d T_s[r] / d Y_i^*(r) = 1/2 ▽²Y_i(r)

d E_H[r] / d Y_i^*(r) = V_H(r) Y_i(r)

d E_ext[r] / d Y_i^*(r) = V_ext(r) Y_i(r)

d E_xc[r] / d Y_i^*(r) = {d E_xc[r] / d r } {dr / d Y_i^*(r)}
≡ V_xc(r) Y_i(r)

其實，總能找極小的問題相當於是在有約制條件（constraint）下的極小化問題，因此必須記得把約制條件的部分以 Lagrange Multiplier 的方式引入（回憶做力學習題時，自由落體與沿斜面下滑之物體兩種狀況其求作用量之最小時的作法不同）。在此問題中約制條件是什麼呢？就是波函數的歸一化條件 N = ∫r(r) dr = S_i∫Y_i^*(r) Y_i(r) d³r。因此，在用上了 Lagrange Multiplier l 的情況下：

d lN / d Y_i^*(r) = l Y_i(r)

綜合上式各項，令斜率等於零，並將 l = - E_i，則得

[H - E_i] Y_i = [1/2▽²+ V_H + V_ext+ V_xc- E_i] Y_i
= [1/2 ▽²+ ∫r(r') / |r' - r| d³r' + V_ext+ V_xc- E_i] Y_i : = 0

這是一個微分方程式型的本徵值問題，可求解各個 E_i及 Y_i 。通常在數值求解量子力學問題的場合，是用有限個正交基底函數展開波函數 Y_i（展開之係數向量為 y_i），把原式化為一個矩陣方程式問題，即

[H] y_i = E_iy_i

別忘了在 [H] 之中有好幾種位勢都是 r 的函數，在一開始尚未知道各 Y_i 時，正確的 r 也是無從得知，必須先猜一組 Y_i⁽¹⁾ 來獲得 r⁽¹⁾，解出 Y_i⁽²⁾ 後再再獲得 r⁽²⁾，一直做到 r⁽ⁿ⁾ = r⁽ⁿ⁺¹⁾ 為止，這叫作自洽場（Self Consistant Feild : SCF）計算。正因為一開始 r（也就是說 [H]）不一定是對的，因此最好避免在這種情況下進行運算代價較高的矩陣對角化，而是使用迭代極小化（Iterative Minimisation）較有效率。

利用梯度找極小

因為是基態，我們所要求解的這一組 Kohn-Sham 波函數，將使的總能的期望值達到最小。前面談到要先猜測一組初始的 Kohn-Sham 波函數再開始解自冾場的問題，當然是極無可能一開始便猜中其解，所幸，即使沒有猜到，Kohn-Sham 方程的 Hamiltonian 也會讓我們得到以波函數為自變數情況下之總能泛函的斜率，這乃是因為 d E[r] / d Y_i^*(r) 具有斜率的意義。因此，一種很有效的方法是把 H Y_i看成是梯度，指引出在波函數的組態空間中 Y_i 要如何改變，才能趨向使總能量最小的波函數。在此沒有看到來自約制條件的 E Y_i，這是因為在數值運算的過程中，我們可以透過不斷地進行歸一化，明確地賦予波函數滿足歸一性保證，故 Lagrange 未定乘子（即 E）不必出現在這個找極小的數值問題中。

得到梯度方向後，沿該方向試作不同步幅的 Y_i修正且比較能量，選定使能量能降到最低的步幅之後，把波函數更新到這個新的值，再找新的梯度，如此周而複始，如下圖 Steepest Decent 所示，程式可以一步一步找到能量極小處的 {Y_i}。

最快下降法與共軛梯度法

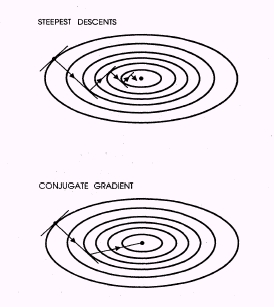
只靠梯度的最速下降法當在遇到狹長的能量地形時，容易造成搜尋方式在山壁兩邊來回振盪，如上圖所示。我們也可以看出兩次的梯度方向之間必定形成直角，會費一點虛功，視問題的本質而定（若能量地形為同心圓，則即使梯度方向也能一次命中）。共軛梯度會參考前一步的方向而避免走直角，具體而言，共軛對於一個理想的 N 維拋物面，只要 N 次搜尋便可以命中目標（見上圖例，二維拋物面只需要兩次。詳見 Numerical Recipes）。因此在己經快接近最低點的時候，那裏的能量地形會因越接近拋物面而收斂效果越好。

預先調節（Preconditioning）

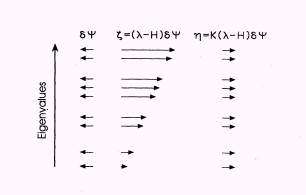
算符 H 會作用在不同的 Kohn-Sham 波函數 Y_i 而得到該波函數所應對應到的梯度方向。然而，H 具有能量的物理意義，因此（能帶）指標 i 較高的態其梯度會被不公平地放大，此問題可透過預先調節的技巧儘可能調整成均勻。下圖 dY 下直排箭頭表示各能帶 i 之波函數與基態波函數（假設知道）之誤差，各軌域被 H 作用後得 z，在調節過後，為 h，可見若以 h 去修正 Y，就會讓下一循環的 dY 很小。如此將提昇找極小的效能。

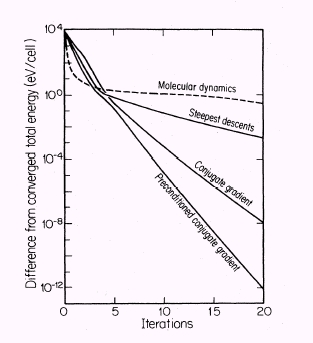
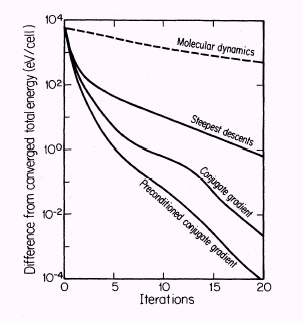
效能比較

橫軸是迭代次數，縱軸是在那個迭代次數所獲得的總能與最終收斂總能值之間的差。注意縱軸是對數座標，降一格代表接近之精確程度再下小數點一個位數。以左圖為例，從第 5 次迭代到第 10 次迭代，收斂位數分別為 1 位、3 位、4 位，可見較精緻的演算法所能帶來的效能提昇是非常可觀的。

Pseudopotential （贗勢）及平面波基底

我們從化學知道許元素的價電子在材料的特性上扮演極重要的角色，內層電子則不然。價電子參與了電荷轉移與鍵結，因此希望解波函數的部分，只處理價電子就好，而將內層電子與原子核的效應合在一起考慮。“贗勢”顧名思義，是一種假的位勢，但它卻能夠表現出原子的離子（原子核 + 內層電子）與價電子應有的交互作用。這是一種很早就由固態物理學家所建立起來的技術，從簡單到複雜的方法都有。

既然是要模仿真正的原子核與內層電子所形成的位勢，其中的兩個中心問題，在於是否能正確獲得：

（一）量子態的能階，
（二）電子雲的分佈。

量子態的能階決定了電子的去處（電荷轉移），而電子雲的分佈表現了化學鍵的類型與強度。這也就是為什麼只要達到這兩點，假的離子就可以模仿真的離子。

贗勢的產生

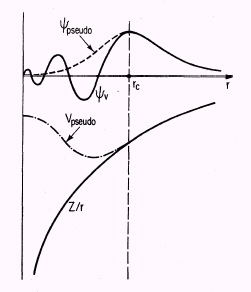
如圖示，實線分別是真實位勢 Z/r 與 All-electron 價電子波函數 Y_v ，我們要取距原子中心 r_c 處為劃分點，r_c 以上波函數完全一樣保留，而 r_c 以內則對波函數加以改造。主要是要把振盪劇烈的波函數改造以一倜變化緩慢的波函數，而它須要是沒有節點的，如虛線的 Y_pseudo 所示。少了劇烈振盪不但允許只以相對很少的平面波來展開波函數，沒有節點的（徑向）波函數也意味著沒有比它本徵值更低的量子態來與它正交。求解內層電子的需要就自動消失了。我們問什麼樣的一個假的位勢能夠在同樣的本徵值的情況下給出 Ypseudo (Y_ps) 這樣的價電子近似解，我們把它叫做是贗勢 V_pseudo (V_ps)。（由於 Y_v = Y_ps for r > r_c，故 V = Z/r for r > r_c）

公式

當原子位勢具有球對稱性（即 V(r) ≡ V(r,q,f) = V(r)），薛丁格方程式可被分離變數，原子軌域則可寫成徑向波函數 R_l(r) 與球諧函數 Y_lm(q,f) 的乘積，其中徑向波函數 F_l(r) = rR(r) 及原子軌域的本徵值 E_l 可從下式（本徵值問題）解得：

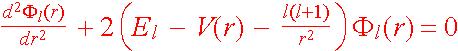
解得 E_l 及 F_l(r) 後，選取 r_c、改造 F_l(r) 為 F_l,ps(r)，並問在什麼樣的贗勢 V_l,ps(r) 之下，原式能重現本徵值 E_l 及 F_l,ps(r)，也就是說 V_l,ps(r) 滿足下式：

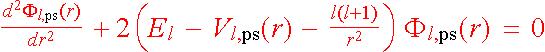
注意上式不再是解分方程的問題，未知函數並未帶有導數符號，只需要移項就可以得到 V_l,ps(r) 。（移項的過程中有除以 F_l,ps(r)，但它沒有節點所以處處不為零，寫在分母沒有問題。）

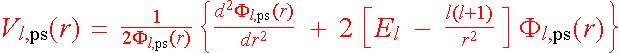
再略為整理一下，得下式（注意等號右邊的量全部都己知，因此贗勢完全可以定出）：

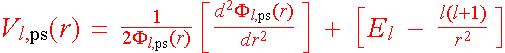
週期性邊界條件

Bloch 定理

與時間無關的薛丁格方程式可寫成

HY = [T + V] Y = E Y

當位勢具有週期性時，如每平移向量 R 時位勢不變

V(r+R) = V(r)

則 Bloch 定理告許我們，原薛丁格方程式的解一定滿足以下的較單形式

Y(r) = u(r) e^ik‧r

這個是新出現的參數，不同 k 就導致不同的解，因此應完整定義成

Y_k(r) = u_k(r) e^ik‧r

其中 u_k(r) 是週期函數

u_k(r+R) = u_k(r)

在這裏的重要結果是，只需要計算一個晶胞（晶胞向量 R）範圍之內的原子與電子即可。

Super-cell 幾何

對於晶體或表面等本身便具週期性的系統，自然非常方便，至於對非週期性的系統，則須採夠大的 super cell 使之分開（而這個 super-cell 所具的晶胞向量就是上一小節所講的平移週期 R）。如圖：

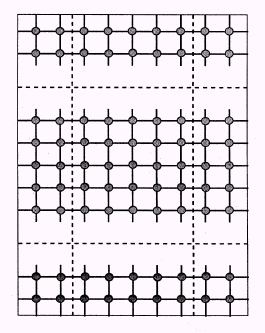
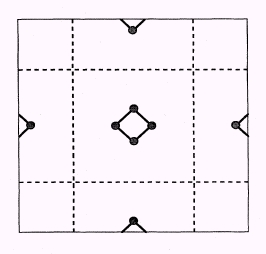
取 super-cell 大小的基本要件是，被模擬的獨立物件要能與其他 super-cell 內的週期性影像隔得夠開，而不致於相互影響而有非物理的結果即可。

如此，我們只須要解 super-cell 波函數 Y_k(r) = u_k(r) e^ik‧r 中的 u_k(r) 部分即可。由於 u_k(r) 是週期性函數，可以很方便地以富利葉級數展開：

u_k(r) = S_G c_k,G e^iG‧r

只需要少數的幾個基底函數，就能把原函數的特徵重現得不錯（若是要精確一點，則可以增加展開使用的基底函數數目）。〈上式的 e^iG‧r 就是平面波基底函數〉一般而言，平面波基底數目的需求端視模擬對象裏們贗勢來決定，此乃因不同贗勢價電子波函數其平滑的程度不同，故所需之基底數也有異。

直接計算原子的受力

某質點在某方向受力，可得自該質點沿該方向移動的（總）位能變化率，這本是力的基本定義。

f_i = - d E(R₁, R₂, ...) / d R_i

然而，根據此一公式，想求出 L 個原子之 3L 個方向的受力則至少需要求 3L+1 次的總能期望值 E，這是相當昂貴的量子問題計算。我們並不採這樣的方法進行能量期望值的偏微分，而是去求能量算符之偏微分（即受力）的期望值。只要波函數的收斂品質夠精確，

Hellman-Feynman 定理告訴我們

f_i = - < Y | dH(R₁, R₂, ...) / d R_i | Y >

使用該定理的好處是，只需要進行一次收斂波函數的量子力學計算得到 Y 就可快速獲得各顆原子在各方向的受力。

Evaluation of the Gradient Operator （梯度算符的求值）

使用基底展開波函數之後，前面的 Kohn-Sham 方程就從微分方程式的型態轉換成矩陣程式的型態。

而扮演梯度算符角色的 Hamiltonian 在這種表象之下就以矩陣型式出現。然而動能矩陣在倒空間是對角化，至於位能矩陣則在實空間是對角化，

[H] = [T] + [V]

不論是表示在實空間或倒空間，總是無法把整個 Hamiltonian 矩陣對角化，

[H_G] = T_ii + [V_G]

[H_r] = [T_r] + V_r

利用 FFT （快速富利葉轉換），要算動能時，把波函數 Y 轉到倒空間（G-space）；要算位能時，則把波函數 Y 轉到實空間（r-space）。如此，進行 FFT ，伴隨轉換後對角元素乘以向量所花的代價是正比於 N㏑ N + N，其中 N 是平面波基底數，這畢竟比直接矩陣乘向量的 N² 要有效率多了。

結合了 FFT、平面波基底展開、（分子動力學法的）迭代極小化這三種關鍵技術，在八零年代由 Car 與 Parrinello 提出 [PRL 55, 2471 (1985)]，成就了高效率與精確度，以密度泛函理論為基礎的量子力學材料計算的時代於是展開。Kohn 也獲頒 1998 年諾貝爾化學獎（Kohn 本人是理論物理學家）。