向量與張量 (I)
向量的定義與基本代數運算
前言:什麼是向量?為何用向量?
別再講 "有大小 、有方向 . . ." , 中學生 level
rotation is not a vector (infinitasimal rotation is)
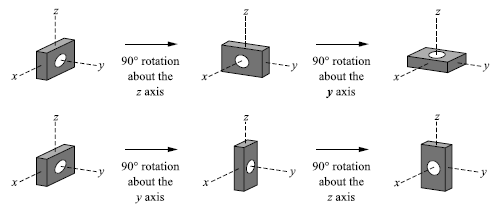
思考:我們如果硬於將轉動當作向量,會導致什麼不妥?加法不可交換,意味著向量 "作圖法" 相加定義裏面的平移律不再適用。
問:那分階段轉動的結果,就沒有數學表示法了嗎?
有同學問到,還有什麼是不可交換的例子。物理上最有名的例子,是 "對 x 微分 算子 (d/dx)" 與 "乘上 x 算子" ,其作用順序不可交換。 另外兩個簡單的例子。對一個任意函數,先乘以二再平方,先平方再乘以二,兩者結果不同。在球面上,+ θ 度出發走 a 距離後,再 以 - 2θ 度方向走 a 距離;與先 - θ出發走 a 距離後,再 以 2θ 度方向走 a ,結果不在同一點上距離。(以上三例請自行驗證。)
解析幾何(引入座標)
向量與純量不同
純量 ex : 溫度分佈、氣壓分佈
向量 ex : 風速分佈
A = A A^ (其中 A^ = A / |A| )
以座標寫出(以分量的方式來表示向量)
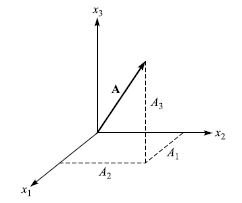
A = A1 e^1 + A2 e^2 + A3 e^3 = Σ Ai e^i
A = (A1, A2, A3)
好處 : 可輕易推廣到高維度 (不然你畫畫看)
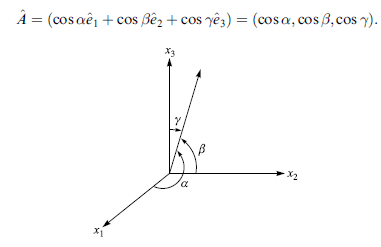
方向角與方向餘弦
單位向量 A^ 可進一步用座標軸單位向量 e^1, e^2, e^3 表示
因為 A = A1 e^1 + A2 e^2 + A3 e^3
因此 A = A (A1/A e^1 + A2/A e^2 + A3/A e^3)
以下列述向量的性質,在解析幾何(非作圖法)下基本運算法則:
向量代數
相等
兩向量相等 iff 其各分量全等
相加
A + B = (A1, A2, A3) + (B1, B2, B3) = (A1+B1, A2+B2, A3+B3)
A + B = B + A
(加數、被加數的一代)
乘係數
c A = (cA1, cA2, cA3)
數或向量都不可以除以向量, 如 c / A 或 B / A
內積
A · B = A B cosθ
也可寫成以分量方式表出
A · B = (A1 e^1 + A2 e^2 + A3 e^3) · (B1 e^1 + B2 e^2 + B3 e^3)
上式如何算出來?使用分配律,並需要用到 座標軸單位向量間內積的結果
e^i · e^j = ?
(對直角(正交)座標而言,特別簡單)
e^i · e^j = δij
Kronecker delta δij
δij = 1 if i = j,
δij = 0 if i ≠j,
故 A · B = Σi Ai Bi
外積
C = A × B
A × B = A B sinθ e^C
e^i × e^i = 0
e^1 × e^2 = e^3
以行列式的方式來寫兩個向量外積 :
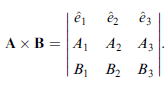
座標軸反轉 (inversion)
polar vector 者:會變號
pseudovector, axial vector 者:不變號
以 permutation symbol(又叫 Levi-Civita symbol) εijk 的方式來寫兩個向量外積:
permutation symbol εijk
εijk = 1 , if {i j k} form even permutation ;
εijk = -1, if {i j k} form odd permutation ;
εijk = 0, two or more identical indices
even 及 odd permutation 的意思(或檢驗的方法) : (從順排 123 ... 起始) 對調兩指標(值) 偶數次能形成的排列, even permutation
(an odd permutation can not be an even permutation )
使用εijk ,有
ei × ej = εijk ek
A × B = Σijk εijk ei Aj Bk
重要關係 Σk=13 εmnk εijk = δmi δnj - δmj δni
純量三重積
A · ( B × C ) = B · ( C × A ) = C · ( A × B )
相當於三個向量張成的平行六面體體積(見下課本圖)
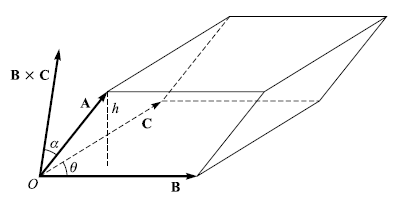
若 corrde. axis vector 逆轉向,純量三重積就會變號,故又被稱為是一個 pseudoscalar (假純量)
(另有一種向量被歸類為 axial vector,又叫 pseudovector,座標軸單位向量 逆轉 下不會變號,不像是一般 polar vector 會變號。若 A、B 是 polar vector,則 C = A × B 中的 C 就是 axial vector。)
向量三重積
A × ( B × C ) = B (A · C) - C (A · B)
問題:那我們怎麼知道,一個量是或不是向量? 換句話說,向量的終極定義是什麼?
(我們都已教了向量的分量如何求得了,還不是定義嗎?)