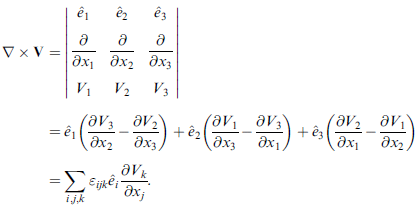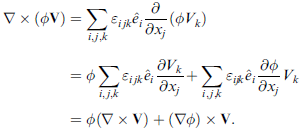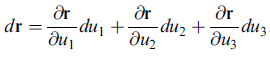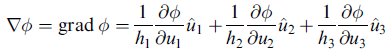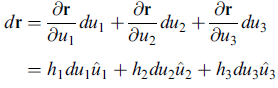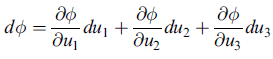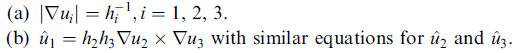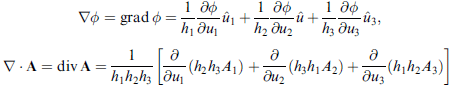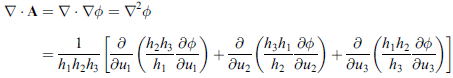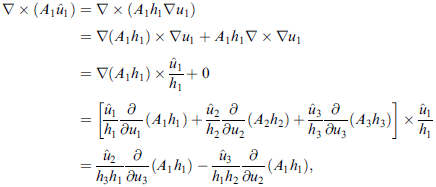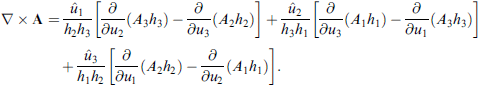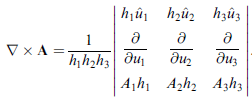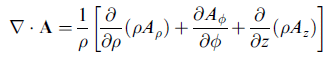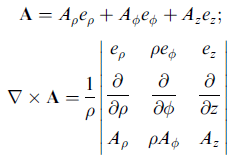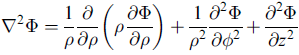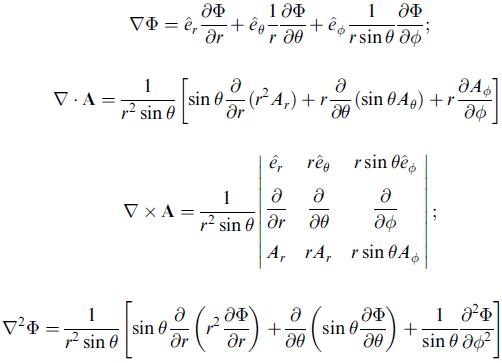純量場微分與梯度
溫度場、高度(海拔)、氣壓場(場是空間的分佈)
保守向量場
W = ∫ab F · ds
保守力作功,僅與初、末位置有關,而與路徑無關。即上式
W = ∫ab F · ds = U(b) - U(a)
這意味著 F · ds = dU,即存在 一 U(x1, x2, x3),其
dU = (∂U /∂x1) dx1 + (∂U /∂x2) dx2 + (∂U /∂x3) dx3
= ( ∂U /∂x1 , ∂U /∂x2 , ∂U /∂x3 ) · (dx1, dx2, dx3) = (∇U) · dr
向量微分算子 ∇ (讀做 nabla 或 del)
∇ ≡ ( ∂/∂x1 , ∂/∂x2 , ∂/∂x3 )
向量場的向量微分
散度
∇· A = ( ∂/∂x1 , ∂/∂x2 , ∂/∂x3 ) · (A1, A2, A3)
= ∂A1 /∂x1 + ∂A2 /∂x2 + ∂A3 /∂x3
是一個純量
散度的意義:
如果一個向量場是由某種 "源" 所產生的,那麼這個場在空間處處的的散度值會突顯出該 "源" 存在與否。
從連續方程式理解 "散" 度
自行見課本說明,會考。
∇2
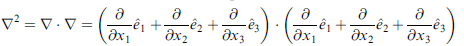
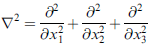
∇2 φ = 0 叫 Laplace 方程式,重要。
∇2 作用在向量場與純量場都可以。
旋度
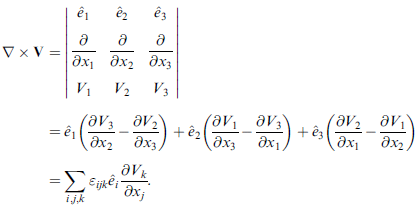
善用 εijk 定義 處理下列證明
∇ × ∇φ = 0
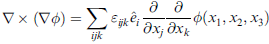
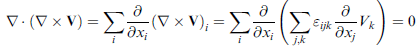
用到 εijk 的反對稱性,也就是 εijk = -εikj 。
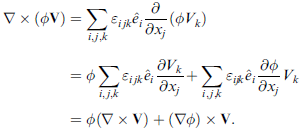
見課本推導,關鍵概述如下:
首先,在不失一般性的情況下,任何座標變換總是存在新、舊座標位置的定義:
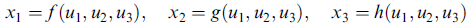
見圖 1.16
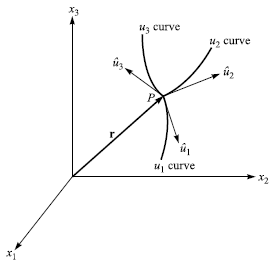
新座標軸的產生
上面這一組的三個函數,會把體的任一點對應到另一點,佈滿三維空間。
這裏如果我們固定住 u2, u3 而只讓 u1 動,就能掃描出一條空間曲線,就可以把它們的切線向量,拿來作為座標軸的方向,就像於前單元採用單一 t 或弧長 s 作為參數時,可定義切線方向及單位切向量那樣。(至於這樣做出來的座標軸單位向量,並不保證正交。)
小線段元素的變換
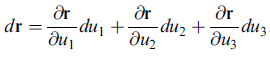
把 ∂r /∂ui 的方向定為 ui^,長度 |∂r /∂ui| 定為 hi (又叫 scale factor),則上式成為
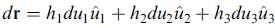
我們現在規定 u^1, u^2, u^3 互為正交,現在再來看小體積元素如何變換
小體積元素的變換

重點是:變換時,乘上 Jacobian。
Jacobian 不等於 0 時,局部有 1對1 轉換 (這是課本提醒)。
(為什麼要講這個?因為未來會有需要把 ∫ f(x,y,z) dxdydz 換成 ∫ f(u1,u2,u3) J du1du2du3 時,就要在微小體積元素上乘上 J。)
梯度算子、散度算子、旋度算子、拉卜拉斯算子的變換 (即它們在非卡氏座標系的公式)
通式
梯度
先看結果公式
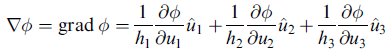
推導起點
假設
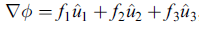
注意 fi 不是本節一開始 談到之 座標變換函數 f, g, h ,而是某函數梯度之分量。
前有
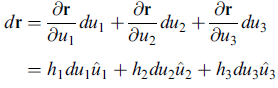
由於 u^1, u^2, u^3 自成一 "正交歸一" 座標系 (這是前提假設),故有 (用上面 ∇φ 的公式與 dr 的公式)
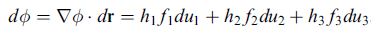
但又根據全微分之基本定義,下式一定成立
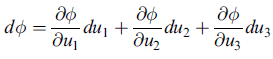
綜合前兩式條件,即得
hi fi = ∂φ/∂ui,即 fi = (1/hi) ∂φ/∂ui
得證原式 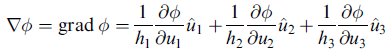
補充:hi 是有幾何學上的意義的,詳見其他教科書。
散度預備
會利用到的兩個關係
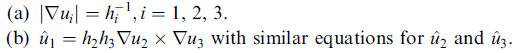
(a) 的證明
利用前已證之 ∇φ 公式,套用在 u1 上, ∇u1 = (1/h1) (∂u1/∂u1) u1^ + 0 + 0 = (1/h1) u1^,故 其長度 | ∇u1| = 1/h1。
(b) 的證明
由 (a) 我們有 ∇u1 = (1/h1) u1^ ,∇u2 = (1/h2) u2^,∇u3 = (1/h3) u3^
∇u2 × ∇u3 = 1/(h2 h3) u2^ × u3^ = 1/(h2 h3) u1^
(為什麼 u2^ × u3^ = u1^ ? )
故 u1^ = h2 h3 ∇u2 × ∇u3 ,得證。
散度
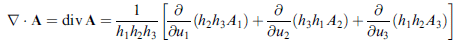
證法
∇ · A = ∇ · (Σi Ai ui^) = ∇ · ( A1 u1^) + ∇ · ( A2 u2^) + ∇ · ( A3 u3^) (分配律)
其中先看 ∇ · ( A1 u1^)
利用前面的 u1^ = h2 h3 ∇u2 × ∇u3 ,有
∇ · ( A1 u1^) = ∇ · ( A1 h2 h3 ∇u2 × ∇u3 )
= ∇( A1 h2 h3) · (∇u2 × ∇u3 ) +( A1 h2 h3) ∇· ( ∇u2 × ∇u3 )
再利用前面的 ∇ui = (1/hi) ui^
上式 = (1/h1) (∂ A1 h2 h3 / ∂ u1) [1/ (h2 h3)] + 0
第二項為零是因為使用了"對任何函數 f, g , ∇· ( ∇f × ∇g ) = 0 " 這一個特性。(同學們自己可利用 ∇· ( A × B ) = ... 的公式證明看看 (用前面 15 條公式之 (4) 和 (6) ),不會做可見 Riley 書。)
(亦可由 ∇u2 × ∇u3 = (u^2/ h2) × (u^3/ h3) = u^1/ (h2h3),
(課文提供的證法,較不方便的點也在此。因為既要證明∇· ( ) 的形式,且尚未證出,就又需要 用到∇· ( ) 的公式。)
補充:也可使用 ∇· A ≡ limΔV→0 (∫CS A · ds ) / ΔV ,即微小體積的通量(向量面積分)來理解 ∇· (u1^) = 0 的理由。
思考:為什麼 ∇不是用向量分量的轉換公式就好,其解果還這麼複雜? 我們把 ∇寫成向量的樣子,操作規則也很像,它到底是不是向量,若不是,為何與向量如此相像?
詭論式的推導
∇ · ( A1 u1^) = ∇A1 · u1^ + A1∇ · u1^
其中,第一項中的
∇A1 = (1/h1) (∂A1/ ∂ u1) u1^ + (1/h2) (∂A1/ ∂ u2) u2^ + (1/h3) (∂A1/ ∂ u3) u3^
故
∇A1 · u1^ = (1/h1) (∂A1/ ∂ u1)
另外,第二項中的
∇ · u1^ = 0
綜合兩項,
∇ · ( A1 u1^) = (1/h1) (∂A1/ ∂ u1)
與剛才上面導出來的不一樣,那裏見到鬼了?
拉卜拉斯算子
前面已知
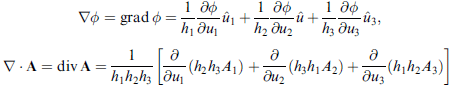
組合使用,可得
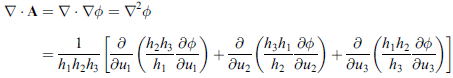
問題:我們怎麼知道上面的操作是合法的?真的可以這樣套用嗎?為什麼?難到沒有一個 "正統座標轉換" ,或是 "廣義微分定義" 的方法,讓我們可以直接看到上述各通式?
旋度
一樣從 ∇× A = ∇× (A1 u1^ + A2 u2^ + A3 u3^) 開始 看 u1 分量
∇× (A1 u1^) = ∇× ( A1 h1∇u1 )
= ∇( A1 h1) × ∇u1 + A1 h1 ∇× ∇u1 = ∇( A1 h1) × ∇u1 + 0
= ∇( A1 h1) × (u1^ / (h2h3))
= Σijk εijk ui^ [(∂/∂uj ) (A1 h1)] [(u1^/ (h2h3)]|k
= Σijkεijk ui^ [(∂/∂uj ) (A1 h1)] [(1/ (h2h3)]k δ1k
= Σij εij1 ui^ [(∂/∂uj ) (A1 h1)] [(1/ (h2h3)]
= εi=2,j=3,1 ui^ [(∂/∂uj ) (A1 h1)] [(1/ (h2h3)] + εi=3,j=2,1 ui^ [(∂/∂uj ) (A1 h1)] [(1/ (h2h3)]
= u2^ [(∂/∂u3 ) (A1 h1)] [1/ (h2h3)] − u3^ [(∂/∂u2 ) (A1 h1)] [1/ (h2h3)]
= [1/ (h2h3)] [ u2^ (∂/∂u3 ) (A1 h1) − u3^ (∂/∂u2 ) (A1 h1)]
(提醒:看到 × 就代入 εijk ,然後設法讓 εijk 消失,是常見的作法)
課本的作法(倒數第二行括弧內應全是 A1 h1 才對)
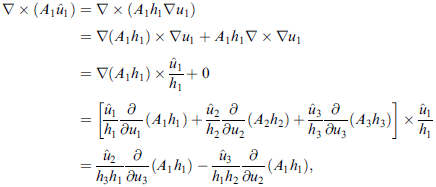
綜合三個部分,完整的結果是:
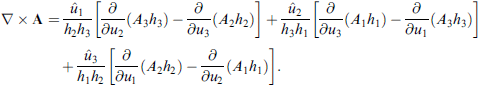
也可寫成行列式形式
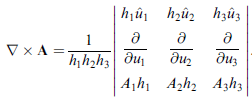
問題:我們怎麼知道前面的 (1) ~ (14) 式對曲線性座標系也是對的?
或先問簡單一點:我們怎麼知道 ,那些公式,在另一個卡氏座標是對的?
∇· v、∇× v 、 ∇v 的不變性(進階)
用張量的語言來了解(不同座標下,形式一樣,張量就是在描述這像的東西。)
一本不錯的小書:J. G. Simmonds, A Brief on Tensor Analysis
柱座標系
(見課本圖 1.17)
x1 = ρ cosφ, x2 = ρ sinφ, x3 =z
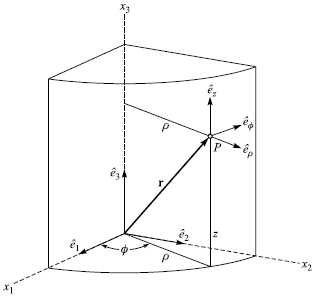
本例中, hrho = 1、hphi = ρ、hz = 1。
證明見下:
方法一
由圖可見
dr = dρ eρ + ρ dφ eφ + dz ez = [1] dρ eρ + [ρ] dφ eφ + [1] dz ez
注意 ρ dφ 的意思。 得證
方法二
由圖可見
eρ = cosφ ex + sinφ ey
eφ = - sinφ ex + cosφey
意謂著
ex= cosφeρ- sinφ eφ
ey= sinφeρ + cosφeφ
此外,從 x = ρ cosφ, y = ρ sinφ 的定義,有
dx = cosφdρ - ρsinφ dφ
dy = sinφdρ + ρ cosφ dφ
現在,從 dr = dx ex + dy ey + dz ez 出發,分別代入上面剛剛整理出未的 ex、eφ 及 dx、dy。就可以把 dr 化成全由 dρ、dφ 及 eρ、 eφ 所構成。
dr = dx ex + dy ey + dz ez= (cosφdρ - ρsinφ dφ) (cosφeρ- sinφ eφ) + ( sinφdρ + ρ cosφ dφ ) (ey= sinφeρ + cosφeφ ) + dz ez
利用 cos2θ + sin2θ = 1
最後,得
dr = dρ eρ + ρdφeφ + dz ez
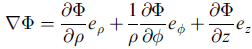
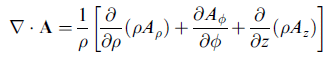
(對行列式乘上一個係數,等同於對其某一行或一列同乘該係數)
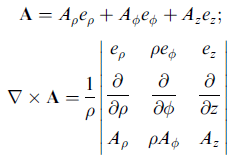
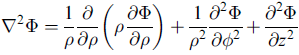
球座標
(見課本圖 1.18)
x1 = r sinθcosφ, x2 = r sinθsinφ, x3 = r cos θ
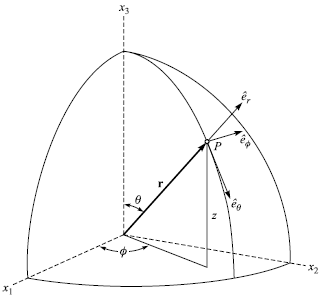
一樣用 ds2 去對出 h1, h2, h3,見課本
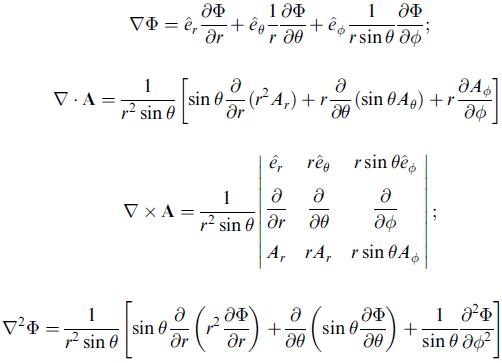
上面的式子雖然很複雜,但數學問題有對稱性時,就會大幅簡化,在未來你們的課程中,這樣的例子很多。
K. F. Riley and M. P. Hobson, Fundation of Mathematics : for the physical sciences, Cambridge University Press
解說清楚,範例眾多。
S. S. Bayin, Essentials of Mathematical Methods in Sceince and Engineering, Wiley
兼具推導詳細與取材完整,
林雲海,基礎數學(簡明版),五南出版社
中文,淺顯易懂