向量積分：高斯定理與連續方程式

 

向量積分

向量的線積分、面積分、體積分。

課本提醒你，當積分的變數個數少於積分子（intergrand 即被積分函數）的變數個數，此一積分就與路徑有關。

除非像右式的純量積剛好是一個全微分 (exact differential) A·dr = ∇φ·dr = dφ ，則該線積分

∫ A·dr = ∫ dφ= φ(b) -φ(a)

與路徑無關 (例如保守力做功)。

 

 

高斯定理

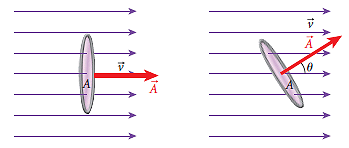
電力線的圖像由法拉第所提出：(1) 電力線起於正電荷、終於負電荷、(2) 電力線越密電力作用越大、(3) 電力線永不相交，這三個描繪 電力線圖像的規則。

 

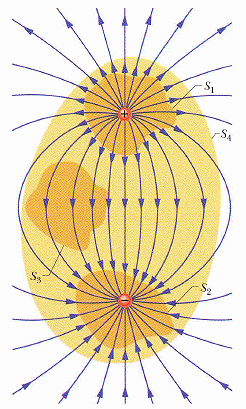
介紹電通量

Φ = E · A

（用內積，即投影，目的在公平地數出電力線數而不受選取面法方向任意性之影響。）

 

電學高斯定律

見普物課本：

ΦCS =∫∫ E · dA = q / ε0

 

一句白話：數電力線數目，就知電荷量。

 

應用：有對稱的電荷分佈，很容易算得電場（不必使用庫倫定律積分）。

 

 

高斯定理（發散定理）（注意定律與定理的不同）

陳述

∫V ∇· A dV = ∫Cls-S A · n^ da

 

證明關鍵步驟：

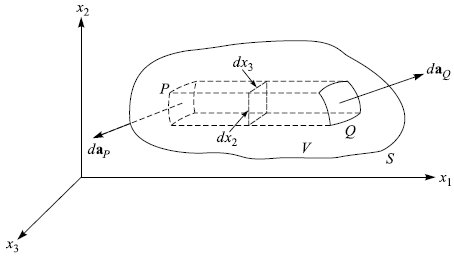
選 x1 為方向，積分一個截面積為 dx2 dx3 的一個長柱子，

在沿者此柱的方向 x1 ， dA1 =  (∂A1/∂x1) dx1

（本來 dA1 =  (∂A1/∂x1) dx1 + (∂A1/∂x2) dx2 + (∂A1/∂x3) dx3，但沿著 x1 方向， x2 與 x3 皆是定在某個值，因此在 dx2 與 dx3 皆等於零的惰況下，(∂A1/∂x1) dx1 = dA1 ）

 

∫V ∇· A dV = ∫VΣi∂Ai/∂xi dV = Σi ∫V ∂Ai/∂xi dV

其中 i = 1的那一項可寫成 ∫CS dx2 dx3 ∫PQ (∂A1/∂x1) dx1

= ∫CSdx2 dx3∫ dA1 = ∫CS  [A1(Q) - A1(P) ] dx2 dx3

 

小面積元素 da1 在 x1 方向上的大小，在 Q 為 dx2 dx3，在 P 為 -dx2 dx3，上式可寫為

∫CS  A1(Q)  da1 - ∫CS  A1(P) da1

 

總合 i =1, 2, 3 三個方向，則

原式 = ∫CS   A(r) · da

得證。

 

以上證明適用簡單連接體（柳丁），若非簡單連接體（如甜甜圈）仍然成立。

 

連續方程式

∂ρ(r) /∂t + ∇·j(r) = 0

，其中 j(r) = ρ(r) v(r)

 

在質量不滅的假設下，可以用高斯定理證出。

 

證明關鍵步驟

從總質量 M = ∫ ρ(r) dV 出發，質量不滅意即 M 為時間上的常數，即 dM/dt = 0

又 dM/dt = ∫CSρv · dS，質量流（通量）之面積分用高斯定律轉成體積分，。

（另法）對小體積元素 dV，它有六個面，在 x 方向有兩個，設分別截在 x 及 x + Δx 。現考慮 流入量與流出量，為 ρ(x,y,z) v(x,y,z) dA 及 ρ(x+Δx) v(x+Δx) dA ，其中 dA = dy dz 。 留在裏頭的淨增率是 ∂ρ(x,y,z) v(x,y,z) / ∂x  乘上 dA，三個方向即 ∇ · (ρv)。積分全體體積即 M 之變化。

把 0 = dM/dt  = (d/dt) ∫ ρ(r) dV = -∫∂ρ(r)/∂t  dV = ∫∇ · (ρv) dV ，此式對任意形體皆對，故有 ∂ρ(r)/∂t    = -∇ · (ρv)，得證。（負號是因定面外為正，而外流質量減少。）

（具體步驟看課本）