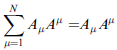座標變換下,向量的分量會消長變化,但向量則保持不變。
物理量中,比向量複雜的量還很多,例如固體的彈性係數("張"量名稱之來源)。我們要怎麼來制定與特定座標系之選定無關的物理量描述方式?(若不在意這個,根本連向量都不必定義了,不過就當它們是不相干的三個數罷了。)
除了物理量本身外,物理量的導數 (各種向量場微分) 也經常出現在公式中,我們也會希望在座標轉換下形式不變。但想達到這一點,一開始就必須採用不同的曲線性座標己有之複雜的通式。
思考:已知向量場微分算子通式較複雜,必須在卡氏座標系才較簡單的情況下,讓我們想想數學形式為何獨厚卡氏座標系?它有何特殊之處?此一特性是否有機會也建構給非卡氏座標系?
張量的定義
與向量一樣,張量也是根據其作座標變換下的轉換規則模式來定義與分類的。事實上,向量也是屬於張量的一種。
從本節開始,我們把向量分量的指標寫為上標

也就是說, x1 = x1(x'1, x'2, x'3), x2 = x2(x'1, x'2, x'3), x3 = x3(x'1, x'2, x'3)
思考:這裏的 x1 = x1(x'1, x'2, x'3) 會是什麼樣子呢?能是什麼樣子呢?
座標變換所使用的矩陣,卡氏座標間要轉換所對應到的矩陣形式很簡單。現在我們問,曲線性座標系呢?公式不可能會一樣了吧?(軸向量的方向隨座標而變。)以下建立轉換矩陣:
當座標變換進行時,座標微小量的變換 (的微積分) 規則如下(重要):
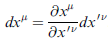
上式中 ν 是要加總的,即 dxμ = Σν (∂xμ/∂x'ν) dx'ν
Einstein's summation convention : 碰到一上一下指標是成對出現時,自動執行該座指標的加總,換具話說,對應該指標的 Σ 符號逕自省略,如下例:
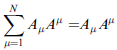
範例:座標軸轉動 θ 角,座標反轉 θ 角
如何記?基底 正交、歸一,把單位向量轉動到另一個單位向量
x' = x cos(-θ) + y sin(-θ) = x cosθ − y sinθ
y' = - x sin(-θ) + y cos(-θ) = x sinθ + y cosθ
∂x'/∂x = cosθ 、 ∂x'/∂y = -sinθ
∂y'/∂x = sinθ 、 ∂y'/∂y = cosθ
延伸:張量在座標轉換的幾何圖像(與向量比較)
二級張量的基本持性,與向量的線性運算
v = v1 e1 + v2 e2
T = Tij
T v = Σij Tij vj = Σij Tij
| T |
|
|
|
|
| T11 |
T12 |
T13 |
v1 |
|
| T21 |
T22 |
T23 |
v2 |
= |
| T31 |
T32 |
T33 |
v3 |
|
把 Ti1 向量轉到 Ti'1,把 T
結論:一個二級張量是(一個線性運作),作用到一個向量上,按該向量的特性,,生成另一個向量。
平面向量
學向量到現在,接觸到的有方向的東西,卻有兩種不同的轉換方式。一種是向量的分量,另一種是切線(常被拿來作為基底向量),但它們的轉換方式卻不一樣:
其中,有一類是循向量之座標分量的規則來作轉換,叫反協變 (contravariant) 向量
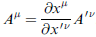
問題:從針對座標微小量而言成立的轉換公式,為什麼對不是微小量的也是對?可以這樣偷渡嗎?
(關鍵是:座標轉換是線性的,故微小向量與一般向量使用同一個矩陣作轉換。)
習題:A'ν 如何以 Aμ 來表示?
另一類,轉換矩陣與上述 contravariant vector 者的結構必須呈倒數,叫協變 (covariant) 向量
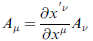
(勘誤:課本上式最右邊的 Aν 應為 A'ν )
純量函數之梯度向量,以及基底向量屬之。
注意轉換公式與指標之搭配情形。
問題:為什麼純量函數梯度的座標轉換就需要這麼轉?(自行驗證)
(光看出現符號的位置,即上下有別)
Aμ 這個符號既是代表分量,我們也常直接用它來描述整個張量。
思考:
之間有何不同?
一定只有兩種?
微小變化,只有 dx 及 d/dx。一個出現在分子,另一個其原本也是 dx,但出現在分母。微分運算只能有這兩種。
反協變向量的範例是:速度、加速度
協變向量的範例是:靜電位梯度(即靜電場)
幾何意義
反協變向量以座標參數的變化(遞增)方向來作為方向參考的依據
協變向量則以正交於等座標曲面方向(即法方向)來作為方向參考的依據
在卡氏座標系下,座標參數的變化恰與等座標曲面法方向一致,故無差別。
補充:
拿同一座標的
A = Aμ eμ= Aμ eμ
其中 eμ· eν = δ μν,它們互為 dual 基底向量
補充:[畫在黑板上]
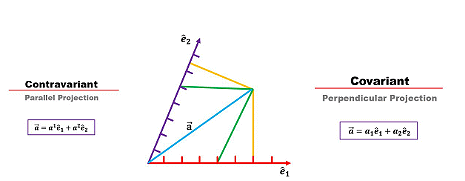
反協變向量 Aμ 為(任意非正交)基底 eμ 的係數,因此用作圖法畫向量的話,是各基底向量乘倍數後,平移頭尾連(平行四邊形表法)。
而與協變向量的分量 Aμ 則是 Aμ= A · eμ 。(注意此處下標的承續沿用) (錐形表法)
想想看在什麼情況下,Aμ 與 Aμ不同? (回憶 A = Aμ eμ= Aμ eμ)
(係數的倍數與投影的長度怎樣會不同,又與向量長度的關係為何?)
Tμν = (∂x'α/∂xμ) (∂x'β/∂xν) T ' αβ
(此式課文沒印成上標,小心)
Tμν = (∂xμ/ ∂x'α) (∂x'β/∂xν) T 'αβ
看清楚有 prime 及 沒 prime 自變數出現在分母及分子位置的規則,不要眼花了。
一個張量所帶的自由指標數目,叫做張量的級或階 (rank)。
![]()
![]()