如何定 (小線段) 長度？
磐古開天（大霹靂、宇宙膨脹），如何想像？
（不是至大無外，至小無內嗎？所有東西的全體既稱為宇宙，則怎麼還能分大小？氣球上畫點的比喻，也無法真正解釋星球之間變遠，因為尺的刻度也隨氣球同步變大。）
（重要）討論至目前為止，協變與反協變並無關聯，除了一點，即從定義來看，它們的內積是不變量，證明如下 (課本印錯：下式中所有 Aβ 應作 Bβ ，最後 Aα 應作 Bα)：
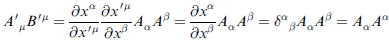
（還好，這套數學至少內建了不變量。我們當然要好好利用。如下：）
而我們最關心的（座標轉換下）不變量是什麼？是 "長度"。
現在，我們要定義長度：
先看熟悉的例子
卡氏座標
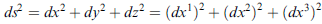
（上式是畢氏定理）
球座標
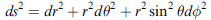
將此形式推廣，至任意（線性轉換）下的座標
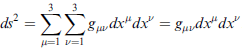
其中 gμν 是矩陣，叫 metric tensor ，其在卡氏座標 及 球座標 中的形式分別為
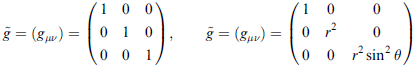
( 補充：其實 metric tensor 個元素可由 基底向量各自內積得到 )
gμν 真的是個張量，證明如下：
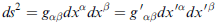
（上式第一個與第二個等號之間，應採下式等號右邊表法較妥，但也不算印錯。）
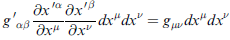
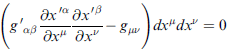
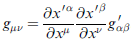
有了gμν後，contravariant 及 covriant 之間便有特定關係
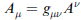
反解上式可求 gμν的反矩陣 [gμν]-1，使有gμν
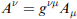
並且由
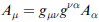
可證
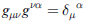
思考：我們定義了測度張量 gμν，它有什麼用？
（黎曼幾何簡介 http://comet.lehman.cuny.edu/sormani/research/riemgeom.html）
前面也曾提到過，弧長的定義如下：
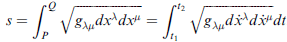
（最右邊之型式，是使用參數 t 的結果。） （最右邊那一項，根號內應無 d 符號，課本印錯）
問，兩點間最短的路徑是不是一條直線？（想想地球儀以及地圖上的航線圖。）
問在一個彎曲的空間中，長度最短的路徑，是滿足怎麼的方程式？
（答案將會是點集合，因此一定是用方程式來寫出。）
求弧長極值（即極小，想也知不可能有極大）
以下推導 測地線方程式，Γαβγ 將出現在測地線方程式中，
以下推導，從弧長極值之條件出發 (什麼是 Euler-Lagrange Equation？)
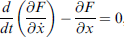
此式之證明在課本習題 1.37 及變分學章節，先採用
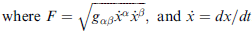
將上極值條件式之各部分分寫開，有
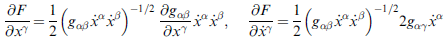
註：上式微分過程中，xα 與 d/dt (xα) (即 x-dot) 視為兩獨立變數，這是因為參數 t 也是任意的。
以及用上了
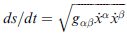，就是用在上式 ( )-1/2 的部分，
則原極值條件式成為
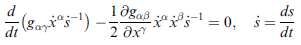
也可表為 (d/dt 微分作用進去)
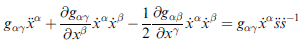
(等號左邊一、二項與等號右邊皆來自 d/dt)
我們藉由以下的關係式
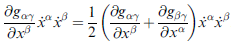
可將原式簡化為
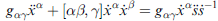
若使用弧長作為參數 即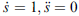 
有
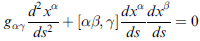
其中已先定義，Γαβγ，叫做克里斯多菲爾符號第一型（三個協變指標）
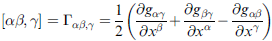
上面以弧長為參數所表示出測地線方程上式， 乘上 gμν （並縮約），得
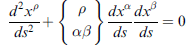
其中
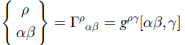
叫做克里斯多菲爾符號第二型（一個反協變、二個協變指標）。如此得到一個型式精簡的測地線方程式。
在平坦空間的情況，Γαβγ= 0，故原式簡化成為
d2 xρ/ ds2 = 0
其通解，顯而易見地，為一直線
xρ = aρ s + bρ
值得注意的一點是，克里斯多菲爾符號 不是 一個張量，其座標變換規則為：
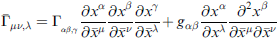
課本介紹這一段，主要是提醒我們：
一、當克里斯多菲爾符號內的分量 不全為零時，在空間不是平坦的。因此它是空間彎曲度的一種指標（事實上是最重要的指標）。
二、即便空間不平坦，兩點間的最短距離這個概念仍是存在的。
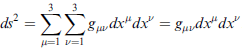
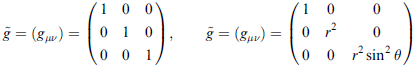
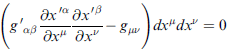
