常微分方程

二階常微方：通解

n 階常係數常微方

其中 p_i 是常數、Dⁿ 是算子 dⁿ / dxⁿ

 

出現在不少物理問題的，是二階的

像很經典的彈簧質量塊、有阻尼、施力振盪，即是上式的型式。

作業：在你的普物課本中，找出力學與電學各自符合上式型式的例子。

 

解法是，先求解以下 homogeneous 方程式

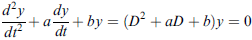
，再找滿足前面原問題方程式的 particular integral，最後兩者合併。

 

 

線性方程式之解的本質

問題：千辛萬苦找到一個解，怎麼知道還有沒有其他解？

問題：只是乘係數再組合（叫線性組合）算不算一個"新"的解？（什麼叫做 "新"？）

問題：有沒有方法從方程式的型式本身就知道其解共有幾個？

 

我們現在要探討的是線性方程式（解）的通性。為簡化起見，在此以上面之二階方程式為例。

若 y₁、y₂ 是二階 homogeneous 常微方兩個獨立的解（意指一個不為另一個的常數倍數）

兩個解呈線性獨立的充要條件是 其 Wronskian 行列式不為零，即：

 

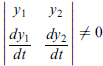
設 A、B 為兩常數，則 y = Ay₁ + By₂ 也是該齊性方程式的解。

同樣地，n 階線性微分方程式的 n 個線性獨立解 y₁, y₂, ... y_n，讓我們可以寫下通解 y = A₁y₁ + A₂y₂ + ... + A_ny_n

 

http://en.wikipedia.org/wiki/Wronskian

 

 

補充：微分方程式之解的存在性證明

思考：一個函數 y 存在，要怎麼證明？（宿命論：一樣東西在這個世界上，要嘛就是有，不然就是沒有，怎麼可能用證明的方法來確認這種問題？）(建構法 ? 矛盾法 ? ...) (可自行找資料閱讀)

常係數二階常微方：

通解

假設我們可以找到一個二階方程式

( D² + a D + b ) y(t) = f(t)

的一個解 y_p(t)，使得

( D² + a D + b ) y_p(t) = f(t)

另外找 y_c(t) ，使得

( D² + a D + b ) y_c(t) = 0

通式 y(t)  是由 y(t)  = A y_c(t) + B y_p(t) 所構成

 

補函數

由 ( a D + b ) y(t) = 0 所誘發，指數函數是解的通用形式

其實對 ( D² + a D + b ) y_c(t) = 0 也是一樣

 

關鍵是

y(t) = e^pt

這個函數型式作為解的主體

 

有 auxiliary (或叫 characteristic) 方程式

p² + ap +b = 0

 

請自行閱讀以下課本中之詳解範例：

 

Ex. 2.9 (實相異根)

 

Ex. 2.10 (虛/複數根)

 

Ex. 2.11 (重根)