常微分方程

二階常微方：特解

特解的規則(Hour 3)

特解不容易直接得到，通常是猜解的函數型式、假設未知常數係數，代入原問題方程式看該未知常係數有沒有解。有解便算猜到，無解就換其他函數型式。

有幾個常見的函數類別的猜測方向，視 non-homogeneous 部分 f(t) 的型式而定，課本共列出七種：

（見課本 如下）

算子 (算符) D

有一種比較直接、少點猜測的 (輔助) 辦法，是學習使用 D 算符 。

D 算符的性質如下：

分配律

線性

結合律

 

觀念： D 就是微分、D^-1 就是積分

 

對於滿足原式 ( D² + a D + b ) y_p(t) = f(x)

的特殊解 y_p(t)，有

y_p(t) = [ 1/ ( D² + a D + b ) ] f(x)

這樣的直接解答

（這麼好的事？快告訴我上式等號右邊如何做下去）

 

使用 D 算符衍伸出規則

(a)

(b)

(c)

 

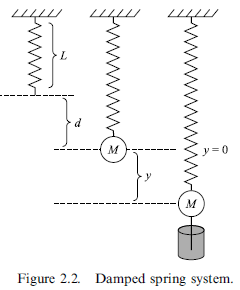
Ex 2. 阻尼振盪

 

 

奧依勒線性方程 (補)

令 x = e^t

簡化為

其中 q_i 全只是常數

 

Ex 2.13 （看了就明白）