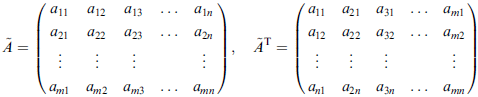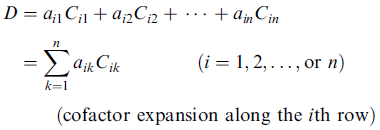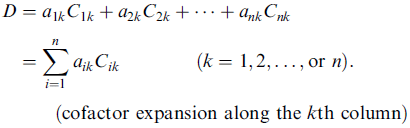矩陣代數、反矩陣求法

更多矩陣操作

 

對易式

A B - B A ≡ [A, B]

在量子力學中重要（測不準原理）

 

A、B 可對易 (commute) ，指 [A, B] = 0

 

A、B 可對易，B、C 可對易，A、C 不一定可對易

 

冪次

A A = A²

 

矩陣的函數

f(M)

矩陣本身是自變數，函數則由矩陣的（具冪次的）多項式構成，如 f(M) = 2M² + 3I 。

 

無窮級數也可以，要收斂才有意義。（至於收斂的定義，則是每個元素都收斂）

例如，e^A = Σ_n=0^∞ Aⁿ / n!

 

矩陣的轉置

定義

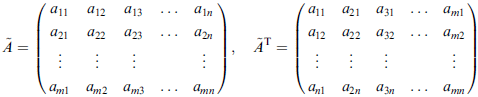
行與列元素全部換成列與行的位置

矩陣說寫就寫下來了，為何還要如此錯亂轉置？

(1) 有些方陣的轉置為自身的反矩陣

(2) 做 dual 向量，內積

(3) 對稱方陣轉置後不變

 

(AB)^T = B^TA^T 、證明

 

對稱與 skew-對稱矩陣（即 反對稱）

對稱矩陣定義

a_kj = a_jk

 

反對稱 或 skew-對稱矩陣定義

a_kj = -a_jk

 

兩對稱矩陣相乘未必對稱

 

任一矩陣可寫為對稱矩陣 R 及反對稱矩陣 S 之和

R = (A + A^T) / 2,

S = (A - A^T) / 2

 

另介紹三角矩陣（有一側，上或下，對角線外元素全為零者）

何須介紹？

1. 求解 A x = b 之 x 快速作法

2. 行列式僅為對角元素積

補充：任何方矩陣 M 可展成 M = L U，L 為下三角矩陣；U 為上三角矩陣

 

純量與向量積的矩陣表法

若 A、B 為行向量

AB^T = BA^T 得一純量

 

A × B 見課本 p.110 （不是特別重要）

 

反矩陣

定義與特性

若方陣 A 能找到一個 B 使得 A B = I （而且 I = A B = B A 一定會成立），則 B 是 A 的反矩陣，反矩陣是唯一的，符號寫為 A^-1 。

 

Ex 3.8 （反矩陣的例子）

 

一個矩陣如果有反矩陣的話，它是唯一的。

(思考：如果這一點不成立的話，會有何不預期的後果？)

(與負負得正有關嗎？)

 

證明：一何矩陣如果有反矩陣的話，它是唯一的。(詳見課文)

證法提要：令 BA = I 且 CA = I,  則 BAC = B(AC) = BI = B 且又 BAC = (BA)C = IC = C (結合律)，故 B = C

 

反矩陣既是唯一，故可記為原矩陣 A 之 A^-1

 

上式用到了若 CA = I 則 AC = I，is it OK ?

 

示範：證明 任何方矩陣 A，A I = I A = A

證明：A I = (A I)_ij  = Σ_k=1ⁿ a_ik δ_kj  = a_ij = (A)_ij = A

I A = (IA)_ij = Σ_k=1ⁿ δ_ik a_kj  = a_ij = (A)_ij = A

故 AI = IA = A 得證。

（此一示範的目的，是讓大家多熟悉矩陣元素與指標相關的數學操作。）

 

示範：證明 若 AB = I，則 BA = I

證明：BAB = B(AB) = BI = B = I B (前已證 I M = M I, for any M)

=> B(AB) = (BA)B = I B => BA = I

The blue part, is it really OK ? (It's OK if B^-1 exists, because we can right mutiply B^-1 on both sides.)

若 AB = I，則 B 必有反矩陣，因為 det(AB) = det(A) det(B) = 1 ，即 det(B) 不為零。

 

作業（重要）：證明 (AB)^-1 = B^-1 A^-1

 

 

反矩陣的求法

公式法求反矩陣：

想法 A A^-1 = I ，其中的第一條 [A^-1]_n1 的部分，有 [A] [A^-1]_n1 = [I]_n1，此時 [A^-1]_n1 是未知數，A 及 I 是已知。

（ (3.22) 式課本符號排錯，請小心。）

即可套用公式解 (Cramer's rule) 求整組 n 個 [A^-1]_n1 值

[A^-1]_jk = cofactor( [A]_kj ) / det([A])

其中 cofactor 翻譯作餘因子， cofactor( [A]_kj ) 定義為  [A] 去掉了 k 列、j 行後的行列式值。

 

從這個解法可看出，若方陣 A 之行列式值不為零，A 有反矩陣。

 

高斯消去法求反矩陣

高中有學，但為什麼它是對的？（有些沒教，故提一下。）

關鍵觀念：線性方程組 [A] x = b 作了 (1) 行交換 及 (2) 列線性組合後，其解不改變。

[A] [A^-1] = [ I ]  -> -> (不變解的情況下，不斷變換) -> -> [ I ] [A^-1] = [ new ] 

猛然驚覺，[new] 正是 A^-1。

行列式

矩陣的幾何意義

一個矩陣的幾何意義，是空間向量之線性轉換（由 n 個向量構成），分別是把 e₁ 到 e_n 單位列向量轉換到由該矩陣的第一個列到最後之第 n 個列所構成的列向量， 對於待轉換的向量不恰為 e₁ 到 e_n 者， 則依基底展開的係數將轉換後的向量比例加總組合之。故謂線性，公式之表法如下：

T(v) = T(Σ_i=1ⁿ v_i e_i) = Σ_i=1ⁿ v_i T(e_i) = v'

 

行列式的幾何意義

則是上述 n 個向量，在空間中所張開來之 n 維體積值。

若這 n 個向量形成維度簡併（如三維時之共面），的情形，則 n 維體積值為零。此一（共面向量組體積為零之）觀念常用在線性方程組求解問題之唯一解、無解或無限多解之判定。

 

3×3、n×n 求法、一般性定義 (Appendix II) p.538

課本附錄 II ：行列式

行列式的定義

 

cofactor Cij 與 minor Mij 的關係

C_ij = (-1)^i+j M_ij

 

Laplace 展開

 

七大性質（課本有提供證明，簡單，必看）

(1)

(2)

(3)

(4)

(5)

(6)

(7)

線性方程組與反矩陣

有 A 的 反矩陣 A^-1，可解方程式 A x = b

A^-1 A x = A^-1 b

x = A^-1 b

 幾個很有用的公式

(AB)^T = B^TA^T

(AB)^-1 = B^-1A^-1

det(AB) = det(A) det(B)

tr(B^-1AB) = tr(A)

det(B^-1AB) = det(A)

det(A^T) = det(A)

 

列 (row) [橫] 、行 (column) [直] ，大陸漢字用法相反。