定義
Hermitian conjugate 為 inverse 者稱之,即 U+ = U-1 者,U 為一個么正矩陣。
(由 一個或一連串么正矩陣所構成的轉換,叫做么正轉換。)
特性
么正轉換下向量的 norm ,即 | v | ,也就是 "長度"
例 : 1/√2 [ [1, i], [i, 1] ]
由於 det(U+) = det (UT*) = det (U*T) = det(U*) = det (U)*
有 det (U+ U) = det det (U+) det(U) = det(U)* det(U) = det (I ) = 1
( 補充 : a* a 常寫作 | a |2 , 同理 v+ v = v*T v = | v |2 )
即 det(U) = eiα ,其中 α 為某實數
前面提過的正交矩陣,是么正矩陣在純實數形的特例。(回憶,OT = O-1, UT* = U-1)
么正矩陣的各列與各行之間,有複數向量的正交關係如下
Σk uik ujk* = δij 、 Σk uki ukj* = δij
在空間中將一個物件以某點為中心轉動(有改變物體的位置),或對座標軸旋轉,而使座標變換(未改變物體的位置),皆可使用矩陣對向量的運算來達成。
以座標軸旋轉,而使座標變換為例,
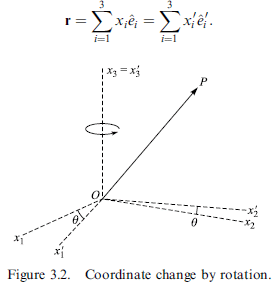
想知道各 xi 與各 x'i 之間的關係,
利用正交關係 ei' · ej' = δij
有 x1' = r · e1'
同理寫出 x2'、x3'
相當於有 (下式僅將 r 以 e 基底展開)
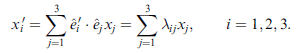 (式 1)
(式 1)
以上建立了座標 x' 與座標 x 的關係式,
注意這裏 λij 是很簡潔地來自轉動前後基底向量(座標軸單位向量)的內積,如下
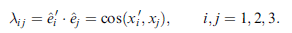
x "旋轉" 到 x' 的表示法,以 矩陣-向量 乘積表示法如下:
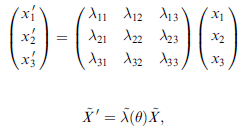
提醒,如果是藉由轉動而把物體的座標軸位置改變,
就是座標位置有變換者,上述公式仍適用。
從
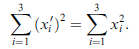
可得(詳見課本)
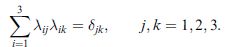
亦即旋轉矩陣行向量間、列向量間 正交歸一。
思考:
線性轉換(如座標軸旋轉)下,會使
可能想法之一:矩陣不是向量,不必遵守向量的座標轉換規則,故不變動。
可能想法之二:我們要維持某些方便的數學規則繼續可以使用,因此矩陣也要跟著轉換。
問題:什麼是那個我們想繼續保有的矩陣規則?
四步分段想法:
(1) 被矩陣作用過後的向量 v 本質上即會是另一個向量 u(即 u = Mv)而非純量等非向量物件。 v 經歷了如座標旋轉般的線性轉換,
(2) 既然 (如座標旋轉般的) 線性轉換 把 v 轉到 v'(關係式 v' = S v),就也會把 u 轉到 u' (關係式 u' = S u)
(3) 前己知,原座標系內(即未轉換下)u = M v
(4) 我們自然是預期 u' = M' v',其中 v' = S v 且 u' = S u'
那麼,要怎樣把 M 變換至 M' 才能保證 u' 的確是 u' = S u 呢?
答案就是,每當向量被乘上矩陣 S 作變換,矩陣 M 就要改造成 M' = S M S-1
如此的確保證 u' 是同一個東西 ,這種對 M 的轉換 S M S-1,叫做 "相似轉換"。
(問題:那原變換矩陣 S 會不會被自己影響到,就不再是 S 而予盾了?答案是不會,因為 S S S-1 = S 仍然一樣,故無予盾。)
特性:在相似轉換下,矩陣-向量 乘積關係式不變。
證明: A R = B r 關係式在相似轉換下不變。
(詳見課本 p.123)
A' = SAS-1、R' = SR,B' = S B S-1、r' = S r
得 A' R' = B' r'
形式不變得證
重要:相似轉換也因此會保守本徵值(即 Ax = λx 的問題,見下節),基於此一特性,它在找一組新基底,而將矩陣角化的過程中,會很有用。

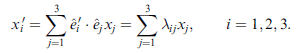 (式 1)
(式 1)![]()
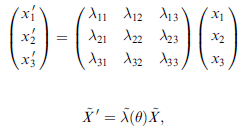
![]()
![]()