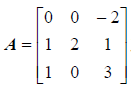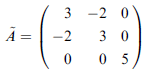本徵值問題與矩陣對角化

數學問題剖析

A x = λ x

其中 A 是已知，而 λ、x 皆為未知。（注意，如此本徵值問題才成立。）

物理意義

什麼樣的向量會被一個線性變換操作後還是自己？

上一節留下的伏筆

 " A R = B r 關係式在相似轉換下不變 "

相似轉換使 A x = λx 變成 A' x' = λx'，注意 λ只是一個數(純量)，因此在 (線性、座標) 轉換下維持不變。

如果 A' 已經是對角化矩陣，那麼 A' x' = λx'  的解根本直接用眼睛就可以看出來：即

A' e'₁ = a'₁₁ e'₁、A' e'₂ = a'₂₂ e'₂、A' e'₃ = a'₃₃ e'₃

[ 上式寫成 column vector 會更清楚 ]

剩下的問題，只是 e'₁、e'₂、e'₃ 這三個 x'， 要怎麼變回 沒 prime ( 即以 原{e'_i} 為基底的) 之 向量 x，那簡單，就是 x' = S x，也因此 x = S^-1 x' 。

所以解本徵值問題，相當於如何透過相似轉換 S A S^-1，把 A 轉成對角化的 A'。

問題是：S 怎麼找？

回顧剛剛的 x = S^-1 x' ，而 x' 只是 e'_i ，可見 S-1 由 x 的解合併構成。[ 寫成 column vector 會更清楚 ]

 

求解步驟

A x = λ x

(A -λI ) x = 0

x 若要是不為 零的普通向量

則必須有 det (A -λI ) = 0

 

求解 λ

 

對每一個 求解出來的 λ_i ，代回 (A -λI ) x = 0，注意 A -λI 現在是已知了，可以解出 x ，可記作 x_λi。

 

Ex 3.12 求矩陣 A = [ [5,4], [1,2] ] 的 本徵值與本徵向量

 

Ex. 3.13 若矩陣 A 的反矩陣 A-1 存在，其 本徵值 為原 矩陣 本徵值的倒數 (1/lambda)，對應的本徵向責則相同。

 

若遇到重根，仍有辦法自同一個 λ 的對應特徵向量中，分離出兩個向量（並可再進一步數學方法 Gran-Shumit 法）。

範例

 

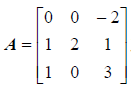
Ex. 3.14 證明相似矩陣有相同的特徵方程式，因此有相同的本徵值組。

（詳解見課本）

Hermitian 矩陣的本徵值與本徵向量

Hermitian 矩陣 的兩個重要性質

(1) 本徵值是實數

Hx = λ x

x^† H^† = ( x^† H) = λ* x^† 

(1) left times x^† forming x^†Hx = λ x^† x

(2) operate on x results in x^†Hx = λ* x^†x

0 = ( λ- λ* ) x^†x

然而 x^†x 不恆為零，一定有 λ- λ* = 0，即 λ 為實數，得證。

 

(2) 相異 本徵值之本徵向量必正交

假設有 Hx₁ = λ₁ x₁ 、Hx₂ = λ₂ x₂ ，則

(1) 式左乘 x₂^† ，得 x₂^† H x₁ = λ₁ x₂^† x₁

(2) 式 取 hermitian 共軛得 x₂^† H^† = λ₂* x₂^† => x₂^† H = λ₂ x₂^† ，

再作用到 x₁ ，有 x₂^† Hx₁ = λ₂ x₂^†x₁

(1) - (2) => 0 = (λ₁ - λ₂) x₂^†x₁

由於 λ₁ ≠ λ₂

x₂^†x₁ = 0 ，得證。

（課本把 dagger 印成加，你應該看出來了）

 

矩陣對角化

用意

不是把非對角元素歸零那般簡單

比較像是把複雜的橢圓方程式，藉座標變換去揮交插相而大幅簡化。

另外，也像是變換基底（座標軸），把線性代數方程式 (3.69) 化為只有對角值非零

 

 

作法

Step 1 : 把各本徵向量 x_λi 歸一化（使其長度或 norm ）為 1  。

註：只想對角化時，長度不歸一亦可，即課本之 S ，但求 S^-1 較麻煩。

 

Step 2 : 並在一起形成 矩陣 R ，則 R 相當是一個座標變換矩陣。

 

Step 3 : 性質由歸一化之本徵值所構成的矩陣是正交或么正矩陣（視元素為實數或複數而定），因此要取它們的反矩陣特別容易。

 

Step 4 : 以此 R 矩陣對原問題矩陣作相似轉換，將使非對角元素變零。

 

性質

矩陣的本徵值，在對角化後出現在對角線位置上，對角線位置上，重根則重複(覆)出現

 

範例 3.16：找出轉換矩陣 S 能使下面矩陣 A 能被對角化

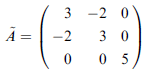
（解法詳見課本）

 

要有線性獨立的歸一化本徵向量，才有機會形成變換矩陣 S

 

範例 3.16：本徵值有重根之情形

有本徵值有重根情形的者，本徵值代回原線性方程組會只留下一條三元一次方程式而非獨立的兩條以上，由於所有滿足單一的一個三元一次方程式的3D點會構成一個平面，一定可以任找兩個向量與法向量垂直（即兩個線獨立關係比例解），來滿足該三元一次式。

 

範例 3.17：證明 矩陣 A = [ [-3,2] , [-2,1] ] 無法被對角化

（詳見課本）

 

 

可對易矩陣的本徵向量

重要定理：可對易的(兩個)矩陣具有相同的一組本徵向量

（證明見課本）

矩陣的 trace 及 行列式值 與 本徵值 間的關係

(1) 一矩陣的本徵值總和即該矩陣的 trace (對角值和)

 

(2) 一矩陣的本徵值連乘積即該矩陣的行列式值

 

(課本表述)

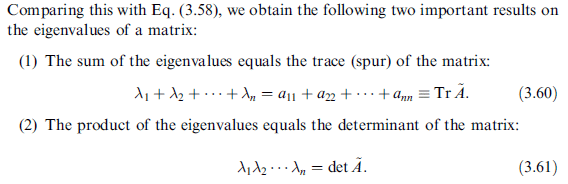
應用

對機械（力學）系統的振動問題，對角化後得頻率，本徵向量為 normal mode 。

 

額外提問：

det (A) = ? del(A^T)