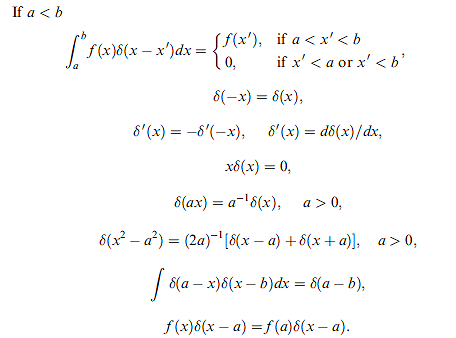δ函數、捲積定理

δ函數

對於任何函數 f(x)，積分 ∫_-∞^∞ f(x) δ(x-a) dx = f(a)

具體說，是 ∫_b^c f(x) δ(x-a) dx = f(a) ， if a ∈ [ b, c ]

∫_b^c f(x) δ(x-a) dx = 0 ，if a ∉ [ b, c ]

其中 δ函數 ，又稱作 Dirac δ函數，具有以下性質：

δ(x) = ∞，for x = 0

δ(x) = 0，for x ≠ 0

 

δ函數 可被下式所表示（表法並不唯一，單峰，圖形下面積為一者皆可）

δ(x - x') = 1 /(2pi) ∫_-∞^∞ e^i(x-x')ω dω

使得

f(x) =∫_-∞^∞ f(x') δ(x-x') dx'

 

我們為什麼要學 它表示；δ-function？

一、理論物理中點狀的場源常用它表示；

二、因為在處理 Fourier 轉換時，要能辨認出它，才有機會化簡數式。

 

定義整理，需熟記：

 

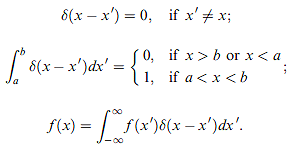
性質整理，有用：

捲積定理

兩個函數 f(x)、H(x) 的捲積 (convolution)，記為 f * H，定義如下：

f * H = ∫_-∞^∞ f(u) H(x-u) du

請注意 f * H 仍是 x 的函數

 

捲積的意義：

蘿蔔田 (一個蘿蔔一個坑) =  一個蘿蔔 * 預挖坑列

http://mathworld.wolfram.com/Convolution.html

物理上的重要應用：X-光繞射之結構因子與原子形狀因子（補充說明）

 

捲積定理

F{f*g} = F{f} F{g}

F{fg} = F{f} * F{g}

（證明不難，見課本）

補充動畫：http://mathworld.wolfram.com/ConvolutionTheorem.html