平衡的條件
力的平衡
Fnet = 0
力矩的平衡
τnet = 0
若是靜態平衡,則還到再加上
線動量為零
P = 0
結構的穩定性
穩定性的定量條件
從力與位能的關係出發,力可以末自位能對位置一次微分,故力對位置的變化就來自位能對位置的二次微分。
Case 1. 穩定平衡
d2 U/dx2 > 0
(向上開 拋物線)
Case 2. 不穩定平衡
d2 U/dx2 < 0
(向上開 拋物線)
Case 3. 自然平衡
d2 U/dx2 = 0
(平坦直線)
重心
重心的定義
作用於某個物體的重力 Fg,是等效於作用於單獨一個點,此點稱為物體的重心 (Center of Gravity, cog)
這裏的等效是指原本組成元素上的受力改移到重心,則原物體也不會有總合力與合力矩的不同,即物體的狀態不變。
重心與質心重合的條件
先決條件是重力場均勻(之前講過了),證明見課本,自己看
找重心的方法
一、吊繩法(為什麼會 work ? )
二、兩指移近法(為什麼會 work ? )
靜態平衡的一系列題例
Bauer
11.1(圖 11.6)翹翹板
(可自行試不同的假想軸心點)
11.2 (圖 11.7)舉啞鈴的二頭肌受力
11-3 (圖 11.8)疊木塊(最多伸多遠出去?)
下圖是真的還是假的?
SP 11.1(圖 11.9,10)雕塑擺放(會不會倒?)
11.4 (圖 11.12)梯上站人(地不能太滑)
課本給大家提示解題技巧,
Halliday
12-1(圖 12-4) 兩秤撐一樑
12-2(圖 12-5)梯子救火員
12-3 (圖 12-6)鋼索與有轉軸之吊桿
12-4 (圖 12-7)比薩斜塔
課本給大家列出解題技巧整理,共九點,可以看一下。
比較關鍵的是:
(一)畫出力圖,施力點與方向皆要明示
(二)寫下水平與垂直力之淨力為零的方程式
(三)選一個施力點作為力矩方程式的轉軸中心
討論
一、走鋼索表演特技的人,有拿長長的平衡桿與沒拿到底差在那裏?
二、單片的梯子是重的還是輕的穩?還是沒差?
未定結構 ( Indeterminate Structures)
未知數的個數比方程式的條件更多,稱為是 "不確定的" (indeterminate)。
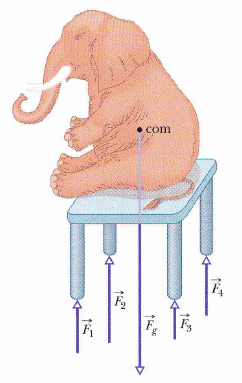
例如,我們這裏有三條方程式可用(平面作圖能處理的問題,有 x、y 分量的淨力都為零,以及物件不受淨力矩,共三個條件),如果有四個未知的力或力矩待求解(如四個桌腳的受力),就會變成 indeterminate 問題(三個腳的桌子反而可解)。
然而,真實世界中這些系統總是有某個力存在,那到底本節的方法中是少了什麼?這個問題的答案是,我們一開始就把物體假設成是剛體,沒有絲毫形變可能及彈性的。
課本提到,不穩的四腳餐桌,我們常會找個紙折一折來墊。如果是一頭大象來坐在桌面上,在桌子沒被坐垮的情況下,我們可以想像四支腳都是結實著地的,因為桌面自然會形變來因應。
要解決這個 "不確定性" 問題的求解,就要引入對物體 "彈性 (elasticity)" 的探討。
例題:12-6 三腳撐地的四腳桌