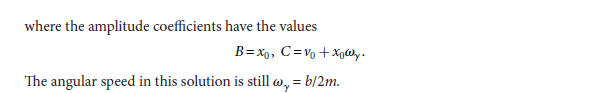回復力的運動方程式
ma = -kx
m d2x/dt2 + k x = 0
d2x/dt2 + (k/m) x = 0
解 x(t) = A sin(ω0 t + φ0) , where ω0 = √(k/m)
代回驗算可以確認的確是解(加上相位角 φ0 就更完整)
另外,也可看影片

初始條件
二階微分方程式一定有兩個待定常數,我們因此預期要有兩個初始值條件,例如:一開始時之位置以及一開始時之速度。如此就恰可以把振幅 A 及相位角 φ0 定出來
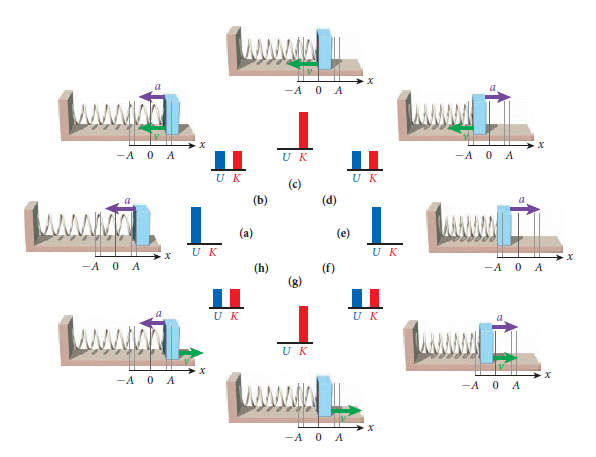
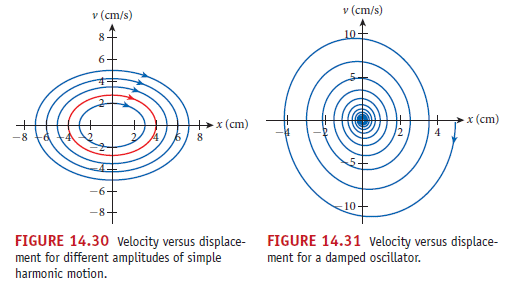
簡諧運動與圓周運動
圓周運動的位置函數 r(t) = ( r cos(ωt + φ0) , r sin(ωt + φ0) ) ,恰好其 x 或 y 分量都構成簡諧運動。
小擺幅(即小擺角)且繩重不計時,可簡化為簡諧運動
從力的分析圖來看
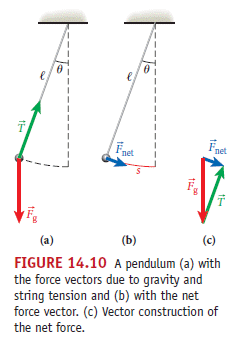

可得角加速度方程式,其形式與前一節 SHO 一模一樣
d2 θ / dt2 + (g / l) θ = 0
我們因此知道解也會有完全相同的形式
推導出上式的過程,請見課本 Bauer Derivation 14.1 或 Halliday 15-6 內文
本來是先得到
d2 θ / dt2 + (g / l) sinθ = 0
至於 θ 與 sinθ到底多接近,從下圖可見
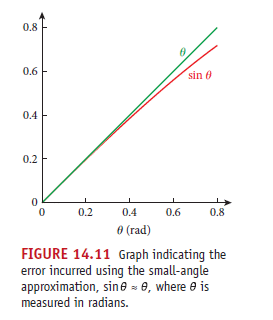
擺的周期與頻率
T = 2π / ω0 = 2π √(l / g)
f = 1 / T = √(g / l) / ( 2π)
圖 14.12 繩長 4:1 的兩個擺(請注意與質量無關),周期為 2:1

例題 14.3 限制了的擺
有摩擦力或是其他能量消耗機制時,會造成減速而終歸靜止,此一效應叫阻尼。
例如,以下系統
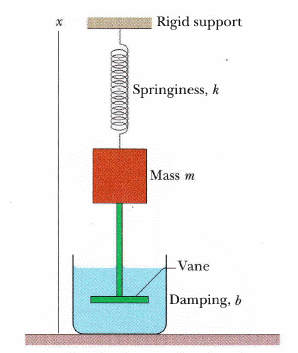
本節探討與速度一次方呈正比的阻尼力
Fd = -b v
,則運動方程式變為
d2x/dt2 + (b/m) dx/dt + (k/m) x = 0
小阻尼
Halliday 課本直接給出小阻尼時的答案

Bauer 課本從比較通解的形式出發,說明若阻尼效應不大,b < 2√(mk),則其解變為

上解只適用於 b < 2√(mk) ,才能使 ω' 根號內為正值。
驗證推導可見課文 Derivation 14.2
對小阻尼,把上兩項收入相位角,一樣得出
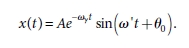
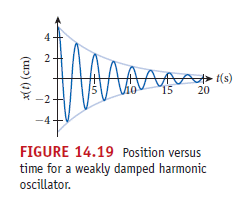
過阻尼
若阻尼較大,即 b > 2√(mk),則有下列結果

臨界阻尼
b = 2√(mk) 的情形,不能沿用前兩種之任一種解法,

例題 14.6 比較 過阻尼與臨界阻尼結果

要讓最快系統回到平衡位置而沒有振盪,要臨界阻尼。如避震器、迴力門(否則等老半天門才關上)。

問題:記憶泡棉是那一種阻尼?為何被拿來作吸收衝擊材質(如高檔電腦內袋)?
阻尼振盪的能量損失
推導 14.3
想法:求能量對時間的變化率(因為已經不再是常數了)

Q 值
定義振盪的品質 Q 為,原總能除以每完成一個周期後的能量損失
Q = 2 π E / | ΔE |
Q 值越大,振盪品質越好。
周期性外力出現在各種現象,如替小孩子推鞦韆、力學(部隊過吊橋)、光學、聲學(震破玻璃)、電磁學都有例子(如微波爐和收音機)。
周期性外力可用以下表示(若非三角函數形式也沒關係,周期性的函數永遠可以用三角函數的級數來展開,求完三角函數的結果再作疊加即可)
F(t) = Fd cos(ωdt)
運動方程式成為
d2x/dt2 + (k/m) x - (Fd/m) cos(ωdt) = 0
其解具有以下的形式
x(t) = B sin(ω0t) + C cos(ω0t) + Ad cos(ωdt)
課本說,B 與 C 可由初始條件定出,比較有趣的是 Ad
Ad = Fd / [m( ω02 - ωd2 )]
ωd 接近ω0 時,振盪會越來越大至無限
真實情況,阻尼力要重新考慮進去
d2x/dt2 + (b/m) dx/dt + (k/m) x - (Fd/m) cos(ωdt) = 0
而上式有穩態解 (steday state solution)
x(t) = Aγ cos(ωdt - θγ)
其中振幅
Aγ= Fd / { [m √[( ω02 - ωd2 )2 + 4 ω02 ωγ2 ] }
就算是 ω0 = ωd 此振幅也不會無窮大,而是
Fd / (2m ω0ωγ)
(記得其中 ωγ 是 damping frequency )
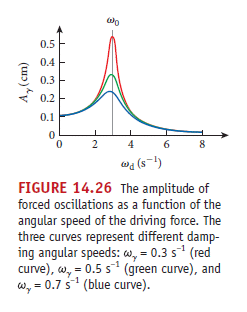
當外來的驅動頻率等於振盪體的自然頻率時,共振就會發生。科技的應用上以及工程的設計上,有時要避免,有時要利用,都是非常重要的。
討論:舉出生活中會遇到之共振共五種
力學、電學中之例子很多。(千禧橋)