理想氣體

 

 

理想氣體的經驗公式

波以耳定律

定溫下

p1 V1 = p2 V2

 

查爾斯定律

V1 / T1 = V2 / T2

其中 T 是絕對溫度

 

蓋–路薩克定律

p1 / T1 = p2 / T2

其中 T 是絕對溫度

 

亞佛加厥定律

同溫同壓下

V1 / n1 = V2 / n2

也就是說

V / n = 常數

 

亞佛加厥數

NA = 6.022 x 10^23

 

 

理想氣體方程式（Bauer-Westfall 課本是以 "定律" 的角度來建立）

P V = n R T

前提假設是，只與容器壁碰撞（也就是分子無體積、之間也無交互作用力）。

 

推導方式：

由前面的幾個定律組合起來（見課本 推導 19.1）

 

範例：以液態氮冷卻氣球（Fig.19.8）

 

恆溫下的理想氣體作功

W = ∫ p dV = (n R T) ∫ (1/V) dV = r R T [ln V] = nRT ln {Vf/Vi}

 

Dalton 分壓定律

不同分子共同構成的氣體，其總氣壓是各分壓之和

ptotal = Σin= 1  pi

只與莫耳分率（即分子數目）有關，也就是說

pi = ri p，其中 ri = ni / n

 

 

能量均分原理（課本是，能量均分定理）

推導：（微觀）氣體分子運動與（巨觀）壓力的關係

L 為邊長立方容積內，分子對一個面所造成撞擊的動量改變是

Δpx = (-m vx) - (m vx) = - 2 m vx

因此分子對容器壁所造成的力，每次撞擊是 2 m vx

然而，每單位的間內有多少次撞擊呢？

容器長是 L，以 vx 的飛行速度，假設 Δt 是每碰一次同一面的器壁所需的時間（碰到另一面的不算），則此 Δt 是 2L / vx

也就是說，每 Δt 的時間內，有 2 m vx 的動量改變

利用 F = m a = m dv /dt = d (mv) /dt = dp / dt

F = dp / dt = Δpx / Δt = 2 m vx / (2L / vx) = m vx2 / L

其他所有分子都算進去

p = Fx / L2 = (1/L2) Σ i=1N Fxi = (1/L3) m Σi=1N vxi2 = (m/ L3) <vx2>avg

<vx2>avg = Σi=1N vxi2

對任何分子，v2 = vx2 + vy2 + vz2

故 <vx2>avg = (1/3) <v2>avg

定義 vrms ≡ √<v2>avg 叫做均方根速率 (root-mean-squire velocity)

總分子數是 N = n NA （其中 NA 是亞佛加厥常數）

p = (mn NA / 3V ) vrms2 = n (m NA) vrms2 / 3V = n M vrms2 / 3V

因此，建立了壓力與均方根速率之間的關係

p = n M vrms2 / 3V

如果把理想氣體方程式當作己知，代入 p V = n R T ，則得 vrms = √(3 R T / M)

pV = W = 3/2 n R T = 3/2 n NA k T = n NA <KE>avg

<K.E>avg = 3/2 k T

 

（補充）能量均分原理

每一個自由度分到 (1/2) k T 的平均動能。也就是說在平衡下，每個分子有 (3/2) kT的動能。

前有 p = (m n NA / 3V ) vrms2 ，故 pV = (1/3) n NA 2 (1/2 m vrms2) = (2/3) n NA [3/2 kT] = n (NAk) T = n R T

也就是說，套用 能量均分原理 就可以導出 理想氣體方程式

從另一個角度來看，p V = n R T 全是由巨觀量所組成，是可透過實驗來驗證的。

 

 

理想氣體比熱

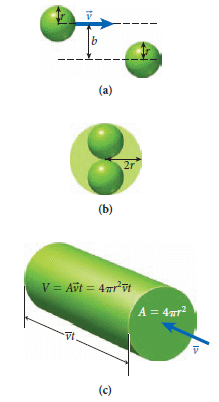
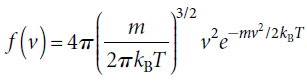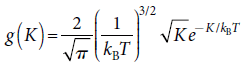單原子氣體

Eint = N Kavg = N 3/2 kB T

 

定容比熱

如何得定容比熱？

依定義 Q = n CV ΔT

ΔEint = Q - W = Q -p dV = Q - 0 = Q = n CV ΔT

由上式 ΔEint = 3/2 N kB ΔT  = 3/2 n R ΔT

故 CV = (3/2) R

對理想氣體

Eint = n CV T

意指 理想氣體 內能只與 n、CV、T  有關

 

定壓比熱

如何得定壓比熱？

再次依定義 Q = n Cp ΔT （定壓下）

由熱力學第一定律 ΔEint =  Q - W = Q - p ΔV 

將上上式 Q = n Cp ΔT 代入並套用前已制定之理想氣體 Eint = n CV T

ΔEint = Q - p ΔV   = > n CV T = n Cp ΔT - p ΔV 

使用 理想氣體 方程式 p ΔV = nR ΔT （定壓下）

n CV T = n Cp ΔT - n R ΔT

可得

CV  = Cp - R

即

Cp = CV  +  R

 

定壓定容比熱之比率

γ ≡ Cp / CV

 

自由度

根據能量均分原理，每一個自由度有 1/2 kB T 的能量

故

Eint = 3 Df  n RT / 2

CV = 3 Df  RT / 2

Cp  則一樣是 Cp = CV  +  R

故比率：

5/3 , 7/5, 9/7 ...

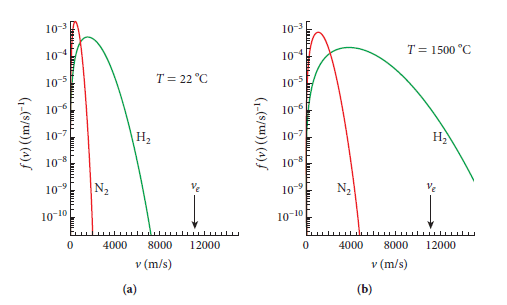
與實驗不同的情況，來自量子效應的差異，要有足夠能量，才能激發該轉動與振動的自由度（振動的能量門檻尤其要高一些）。

 

課本的討論法，是只考慮移動與轉動，而把振動當作額外的考量。此一作法，與把能量均分不看作是原理的作法是相互應的，也就是說，只在理想氣體的層級下建立能量均分（事實上，課文中也使用了原理這樣約名稱來賦予每個多出來的自由度 1/2 kB T 的平均能量）

因此，課本對多原子分子氣體的討論方法如下：

有完整的三個方向的運動，以及三個軸的轉動，共六個 "自由度"，因此，CV = 6/2 R = 3 R，γ = 4/3

 

 

理想氣體的絕熱過程

所謂的絕熱過程就是 Q = 0，故 ΔEint = -W，若系統是理想氣體，則過程中

p Vγ = 常數

其中 γ ≡ Cp / CV

證明推導請見課本 推導 19.3

上面公式不要跟 pV  = nRT 混淆在一起。

推導雖然有點複雜的，但本式允許我們在不知道（或不用管）溫度的資訊下，掌握理想氣體作功時其壓力與體積的變化，這是很有用的。

我們為什麼要關心 " 理想氣體" 的 "絕熱過程"？

這是因為引擎是氣體在做功，而它運作得很快的時侯/部份階段，可視為絕熱過程。（不要誤解這裏必須忽略廢熱的問題，廢氣的排熱要比引擎的排熱多。）

 

在建立了

p Vγ = 常數

後，代入 p V = n R T 去可置換出 V、T 關係

p Vγ = 常數 = p Vγ = (p V) Vγ-1 =  n R T Vγ-1

即

T Vγ-1 = 常數

（上式可以解釋冷藏的碳酸飲料間瓶後，瓶口會凝結並有霧氣。）

 

例題 SP 19.1：腳踏車胎打氣一下問昇溫

 

 

 

 

氣體動力論

Maxwell-Bolzman 速率分佈

 

H2 為何在大氣中這麼少？（前面重力張節有，地表附近的脫離速率是秒速 11 公里左右。）

大氣層有一層（100 公里以上）其溫度可高達 1500 度，叫 thermosphere ，而氫比其他大氣成份更易飄向高處。因此氫會跑掉，氮不會。

 

Maxwell-Bolzman 動能分佈

 

對於 N2 在不同溫度下的分佈，取對數座標的結果。注意這樣的取法可以協助我們得到指數部分，因此在本例中，圖的斜率就會是自變數的係數。

 

我們因此知道，氣體的動能曲線可以拿來作為溫度的指標。（在此雖並未考慮相對綸效應，以最快的氫氣在 1500 K時，速度最快也才每秒 15 公里，見上上圖。這才相當於每秒 30 萬公里光速之 0.005% 。另外，理想氣體所作之分子間不交互作用的近似，在考慮大氣也是合理。故很多大氣層性質可用Maxwell 的分佈來了解。）

例題：夸克–膠子 電漿的溫度（圖 19.21）

太陽中心溫度 1.5 × 107 K ，意味著平均動能 2 k eV （用 3/2 kB T 去算）左右，但質子核融合所要克服的電位能約要 1MeV ，因此只有速率分佈尾部約高速、高動能質子能促成反應。（事實上，雨水形成也是如此，不是靠沸騰，而是少部分高速水分子。）

 

平均自由路徑

氣體中每個分子都不斷的碰撞而改變方向，擴散相關性質與一個分子 "平均直走多遠是後才被撞到" 有關。

平均自由路徑 λ 與密度 N/V 有關，N/V 越大 λ 越小；另外，分子截面積越大， λ 也越小。

推導的觀念如下，

單位時間用勢力範圍掃出的體積，拿它飛行的長度除以應該要落在該體積內的分子數，即為可自由飛行而不碰撞的距離。

由於分子是在動而非靜止，相對速度 v;rel = √2 vavg 要用上（如何證明這一層關係？）

λ= 1/ [ √2 (4πr 2) N/V ]

或再套用理想氣體方程式

λ= kBT/ [ √2 (4πr 2) p ]

作業：上式的證明（詳見課本）

進階思考：如果我們用速率分佈來更嚴密地計算平均自由路徑，其結果會不會還是一樣？

例題 19.6 ：空氣分子的平均自由路徑