奧圖 (Otto) 循環
德國工程師奧圖將一理論家提出的設計實作
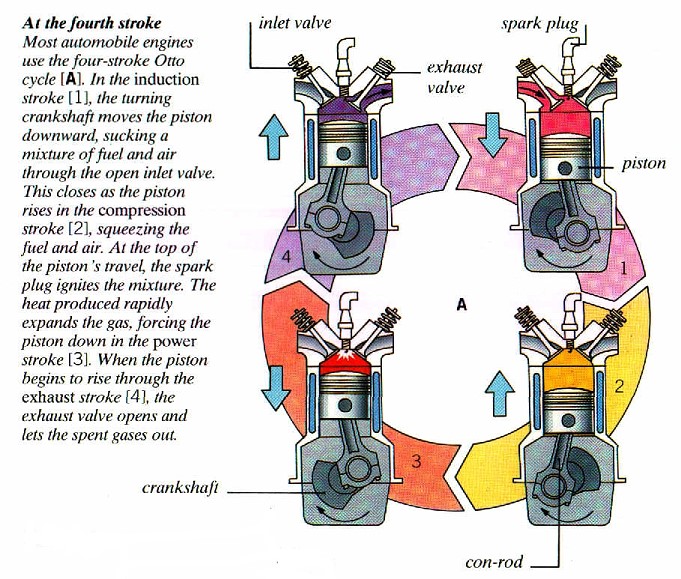
汽油引擎
注入、壓縮、點火爆炸、排氣
震爆問題
活塞推到盡頭時,才點火,這是運轉最順利的情況。否則活塞還在朝向火星塞推,就提早點火,這會造成力量對衝,也就是引擎震爆的來源。何時引燃的問題
辛烷值
燃料分子的特性(如長鍵狀、分叉狀)會影響壓縮到什麼程度就要點燃約最佳(無震爆)時機,這會影響引擎設計上的壓縮比,也因此決定馬力的大小。
有鉛汽油
四乙基鉛的添加可抑制震爆,換來引擎的調整而得到馬力的提昇,但這樣對環境(人體)有害。
無鉛汽油
觸媒轉化器可消除 CO, NOx 等
迪索循環
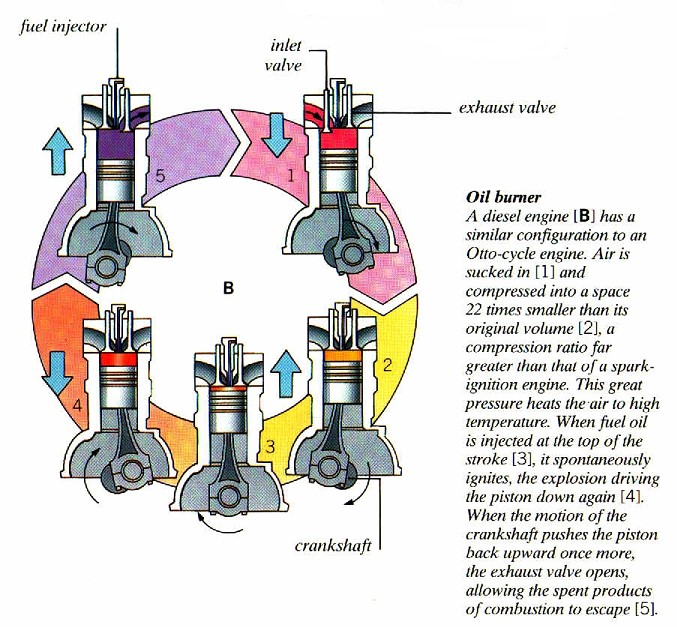
柴油引擎(較汽油引擎有更高的壓縮比)
注入、壓縮、自燃(不用火星塞)、排氣