電荷移動所造成的磁場

上一個單元談磁場對運動中電荷的作用，本章一開始則討論磁場如何由電流造成。

問題：用電磁鐵把重物吸起來，線圈上的電流作功多少？（另一種問法）

必歐－沙伐定律 ( Biot-Sarvart Law )

小電流線段元素在空間中的一點產生多大的磁場

dB = (μ₀ / 4π) i ds × r / r³ = (μ₀ / 4π) i ds × r^{^} / r²

其中 r^{^} 是 r 的單位向量

回憶 庫倫定律 電場

dE = ?

電流分佈造成的磁力

長直導線

關鍵是，使用積分（見課本），結果是

B = μ₀ i / (2 π r_⊥)

請大家要注意圖像的建立

 

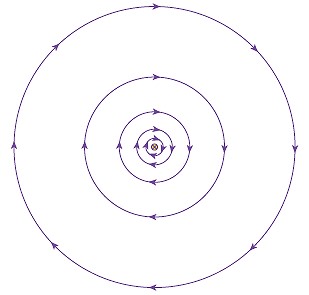
平行導線

利用

B₁ = μ₀ i₁ / (2 πd)

與

F = i L × B

可以得到 2 號電線的受力為，

F_1→2 = i₂ L B₁ = i₂ L [ μ₀ i₁ / (2 πd) ] = μ₀ i₁ i₂ L / (2 πd)

另一條線的受力是，大小相等、方向相反。（電流越大、距離越近，力越大）

 

 1 安培的定義

SI 制的安培是定義為

無限長直而可忽略半徑的導線，通電流是各 1 A 且相距 1m 時，會產生 2 × 10^-7 N 的力。

如此則μ₀ 就有精確的定義，為

μ₀ = 4 π × 10^-7 T m / A

 

例題 28.1：迴圈的受力

例題 SP 28.1：電磁軌道加速器

 

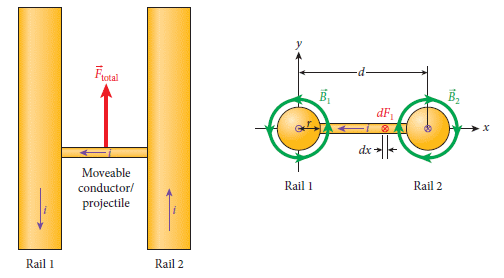
圓形環路所造成的磁場

以圓形線圈造出磁場的例子十分普遍，現在來了解一下。

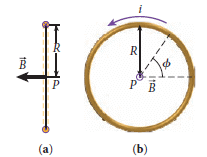
利用 必歐－沙伐定律：

dB = (μ₀ / 4π) i ds sin 90° / R² = (μ₀ / 4π) i ds / R² = (μ₀ / 4π) i (R dθ) / R² = (μ₀ / 4π) i dθ / R

積分得

B = ∫ dB = ∫₀^2π(μ₀ / 4π) i dθ/ R = (μ₀ i / 4πR ) ∫₀^2πdθ= (μ₀ i / 4πR ) 2 π= (μ₀ i / 2 R )

結論是，半徑 R 越小、電流 i 越大，中心點磁場越大。

 

如果想知道中心軸上的磁場強度，則要處理圖中來的  dBx 分量並積分（dBy 因對稱性關係會抵消所以不必處理）

，推導細節見課本。

安培定律

小量電荷元素的靜電場有庫倫定律，非常複雜們分佈用電腦處理，至於較對稱的電荷分佈則有高斯定律可利用。（回憶磁場高斯定律與磁單極不存在之關係）同樣的，小電流元素有必歐－沙伐定律來預測空間中處處的磁場，非常複雜們分佈一樣得用電腦處理，對於高度對稱的電流分佈，我們則有安培定律來幫忙簡化：

∫_CL B · ds = μ₀ i_enc

其中 積分範圍是封閉迴路 (Closed Loop) ， i_enc 是迴路中的淨電流。

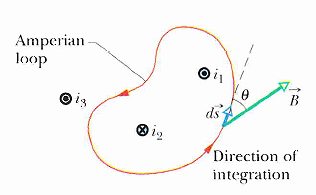
以下是各種電流幾何的例子：

 

載電流長直導線的外部磁場

∫_CL B · ds = B ∫_CL ds = B (2πr) = μ₀ i

B = μ₀ i / 2πr

 

載電流長直導線的內部磁場

假設內部電流密度均勻，則姑妄培定律給出

B (2πr) = μ₀ i (π r² / π R²)

B = ( μ₀ i / 2πR²) r

其中 R 是長直導線半徑，r 是與軸心距離。

 

螺線管 (Solenoid) 與 螺線環 (Toroid)

螺線管的磁場

見下圖 H FIG.29-18, 19, 20

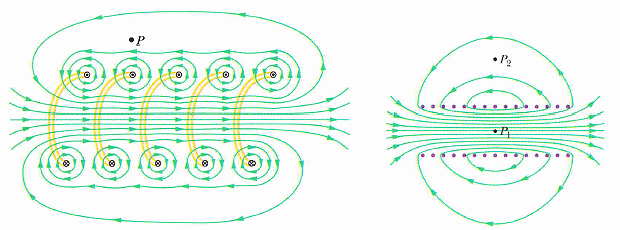
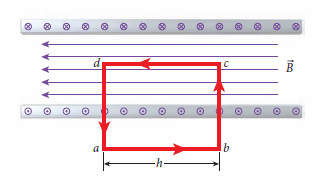
d-a 與 b-c 段都因為磁場沿著對應的迴路線之上並沒有分量而等於零。另外，a-b 段磁場，課本的說法是理想（無限長）螺線管

B = μ₀ i n

n 是單位長度之匝數 (number of turns)

 

螺線環的磁場

見圖 (H FIG.29-21)

B = ( μ₀ i N / 2 π ) ( 1 / r )

原子就是小磁鐵

軌域（軌道）角動量貢獻

i = e / T = e / (2πr / v ) =  v e / (2πr)

μ_orb = i A = v e / (2πr)  (πr²) = v e r / 2

另外

L = r × p

L_orb = r p = r m v = r m (2 μ_orb / (e r) ) = 2 m μ_orb /  e

最後

μ_orb = - e/2m L_orb

 

例題 28.3 氫原子 的軌域磁距

 

自旋 (Spin)

量子效應，電子、質子、中子都具有自旋量子數

s = 1/2

其自旋角動量是

S = h √ [s (s+1)]

可定任意選定的 z 方向投影是

S_z = h / 2 or - h / 2

則自旋磁距與自旋角動量若關係是

μ_s = g q /(2m) S

其中 q 是電荷數，g 是旋磁率。

 

物質的磁性

前面曾提到，一個磁偶極在磁場中會受力矩被偏轉趨向磁場方向，如此能量才會比較低。現在來考慮物質在磁場中所受的影響。

因為原子與電子軌道有磁性（一個像載流電線，一個像永久磁鐵），因此在外加磁場下會被誘發另一個（內部）磁場，我們稱作磁化 M：

磁化

B = B₀ + μ₀M ≡ μ₀ ( H + M )

即

H ≡B₀ / μ₀

 

順磁 與 反磁

M = χ_m H

χ_m 見表 28.1

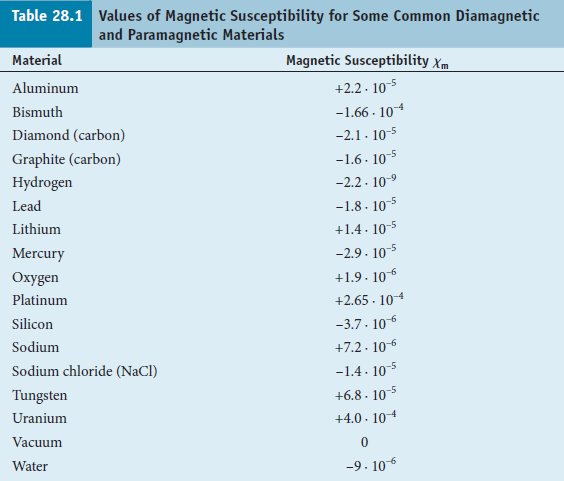
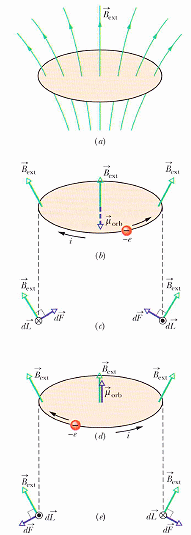
χ_m < 0 的材料叫反磁性，在磁場下這類材料所誘檔出來的磁場

 

以環路電流來示範反磁性物質受下方強磁極不均勻磁場的向上排斥力

 

鐵磁

科學玩具：居禮引擎

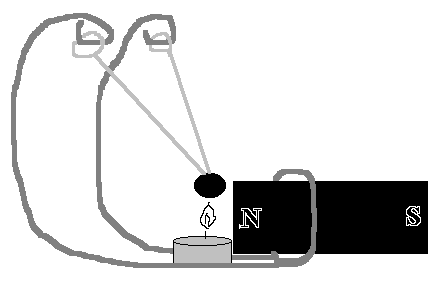
應用：大同電鍋的溫度自動切換

超導體的 Meissner 效應

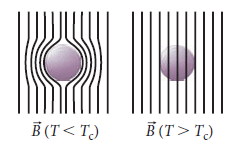
物理玩具

Buckyballs

http://www.youtube.com/watch?v=mJWJXaWz94k

http://tw.myblog.yahoo.com/specialyvonneliu-specialyvonneliu/article?mid=1863&sc=1