相對論

速度相加的問題

直接關係到我們時、空的宇宙觀

對物理定律在不同慣性座標系下一致，也是基本預期

 

馬克斯威爾方程式

四條一組的馬克斯威爾方程式

電磁波的波速

整理後變成波動方程式（詳見課本推導 31.1），波速因此直接出現在公式中

其中

 

光的介質：以太？

聲音的傳播媒介是空氣或可振動的物質，當時料學家也理所當然認為有專門傳播光的介質，甚至先命名它為以太。

找尋以太

邁可森－莫利的干涉儀

來自同一個光源，分出的兩道光路後再讓他們干涉在一起，若光程稍有變化，就有干涉條紋變化。如此，想像一條光路與以太風的方向平行，另–條光路垂直。稍作分析即可知光程不同。現在想像將整個儀器緩緩旋轉 90 度角，使兩條光路角色交換，則我們預期要看到干涉條紋變。

 

最成功的失敗實驗

儀器之靈敏度已改進到非常好（遠超過所需，地球公轉速度每秒數公里），只要有對以太的相對運動一定測得出來。但還是無任何結果，仿彿以太在地球週圍是靜止。

勞倫玆縮短理論

沿著對以太運動的方向，長度縮短

L = L₀ √(1 - v²/c² )

恰好可以符合邁可森–莫利實驗，但爭議性很大。

愛因斯坦的相對論（相對性原理）

基本假設：

（一）所有慣性（即不加速的）座標系中，物理定律不變

（二）光速對任何觀察者皆相同

 

β 與 γ

這兩個量常在相對論中見到，先定義

β = v / c

γ= 1 / √ (1 - β²)

光錐

任何訊號與交互作用不能超過光速，因此某一時空點能影響到的範圍，有一個新的邊界限定，叫正光錐；而所有能影響到該時空點的部分，則叫負光錐。

見圖

上圖中，紅點只能影響藍點，而與綠點完全不會有因果上的相關性。同理，過去所能影響到現在的（事件）點，也只在一定距離範圍之內。

 

古典物理：

兩空間點的相距（不論那個觀察者看到）

Δr = √ [ (x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)² ]

（注意：上式在座標變換下其值不變，即座標轉換保長）

 

兩時刻點的間距（不論那個觀察者看到）

Δt = t ₂ - t ₁

 

相對論：

兩事件點在時空中的間距（不論那個觀察者看到）

s² = c² (Δt)² - (Δr)²

 

時間增長

Δt = γΔt₀

Δt₀ = 2h / c

Δt = L / c

其中 (L/2)²= h² + (x/2)² 故 L = √(4h² + v²Δt²)

則 Δt = L / c = √(4h²/c² + v²/c² Δt²) = √(Δt₀² + v²/c² Δt²)

即 Δt √(1 - v²/c² )= Δt₀

Δt = Δt₀  / √(1 - v²/c² )

即 Δt = γΔt₀ 

 

長度縮短

L = L₀ / γ= L₀ √(1 - v²/c² )

重現了勞倫玆提出的的假說公式

科學沒有因此而搞亂，物理定律的位階反而更加穩固。

推導（見課本以太空梭為例）

靜止時機身長 L₀ 的太空梭向前飛行速度 v，量其機身長度 L

在靜止座標系置 雷射與計時器，機鼻擋住 光束啟動計時，機尾離開時計時停止，則 L = v Δt₀ ，其中 Δt₀ 是 proper time（此一時鐘沒有在運動）。另外， 從機內人觀點而言，看機外鐘的讀數固然是 Δt₀，但若使用置於機內的時鐘則有時間膨脹效應 Δt  = γΔt₀，因此光束被擋住（先遮後放）的整個流程耗時 Δt  ，他看到光束照射點走了 v Δt 的距離，長度恰是機身長 L₀ 。

種總而言之，由於有時間膨脹效應，機內鐘計得之時間 Δt 比機外鐘計得之時間 Δt₀ 長，關係為 Δt  = γ Δt₀，故 我們有

L = v Δt₀

L₀ = v Δt = v γ Δt₀

得 L = L₀ / γ

故量得之機身長縮短 1/ γ 倍

 

孿生子矛盾

予盾點：太空（高速）旅行回來，兩個都比對方年輕，矛盾。

解釋：坐太空船的，要折返回來的那一個較年輕，分別從地球觀點與太空船球觀點皆如此。

作法：利用前面已推得的時間延遲以及長度縮短

本問題之  γ 值為 1/ √(1- 0.65²) = 1.32

地球人看：太空船 0.65 倍光速向右， 抵達 3.25 光年處後原速折返，單程費時 5 年，故 10 年返抵地球 。地球上的人也知道太空船上時間流較慢，10年 / γ= 船上年，入代 γ 值 得 10 年/ 1.32 = 7.576 年。

太空人有在移動，在他看起來距離 (有長度縮短) 單程為 3.25*1/1.32 = 2.462121... 往返總長 4.9242...          (而不是 6.5 光年)，故其行程費時 4.9242 光年 / 0.65 光速 = 7.576 年。

 

 

請注意返航時速度是 -0.914 c ，而不是兩倍 0.65c 的 -1.3 c 。

（請閱讀課文 pdf 共三頁）

 

新的速度相加公式

不再是 u'_x = u_x + v

而是（推導見課本）

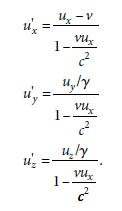
相對論頻率偏移

頻率與時間有關，狹義相對論告訴我們，有相對速度的發射體，由於時間間隔改變，因此頻率也會改變。這與聲學都卜勒效應的原理是不同的。

詳細推導見 http://en.wikipedia.org/wiki/Relativistic_Doppler_effect

設相互遠離

從光源的觀點，從第一個波前恰達到接收者，此時第二個波前距接收者 λ那麼遠。

要讓第二道波前以光速 c 追上接收者，但接收者也同時以 v 後退中，追上（第二波前被接收到）時第二波前還要走 λ+ v t₀ 這麼遠，是以光速 c 來走的，有以下關係式

λ+ v t₀ = c t₀

共費時

t₀ = λ / (c - v)

此 λ為波長，故有 λ = c / f₀，因此

t₀ = λ / (c - v) = (c / f₀) / (c - v) = 1/ [(1 - β) f₀]

接收端是移動中的，故時間過比較慢，此一事件之歷時 t₀  對接收端而言會較短

t = t₀ / γ

故

f = 1/ t = γ[(1 - β) f₀]

= [(1 - β) f₀] / √ [(1-β) (1+β)]

= f₀ √[ (1-β) / (1+β)]

= f₀ √[ (c -v) / (c + v)]

 

(遠離時)

f = f₀ √ [ (c-v) / (c+v) ]

 

(接近時)

f = f₀ √ [ (c+v) / (c-v) ]

 

(transversive)

 

勞倫玆轉換

明顯與伽利略轉換不同，時、空是同為量的兩個分量（同步消長，像旋轉一般），故時空是一體的。

 

伽利略轉換

x' = x - vt

y' = y

z' = z

t' = t

 

勞倫玆轉換

x'  = γ ( x - vt )

y' = y

z' = z

t' = γ ( t - vx/c² )

 

勞倫玆轉換下的不變量

作業：驗證前面所定及 s 是一個勞倫玆轉換下的不變量

 

以不變量來寫物理定律公式

（才能真正突顯公式中各物性或量的特徵，而不只是舊式新寫。）

在相對論考慮下，向量都是四維的，而物理定律則形式上要滿足勞倫玆轉換不變性。

其長度（絕對值）會滿足勞倫玆轉換不變性的物理量，如：（但絕對值定義裏的平方和）要用 - + + + 係數，叫閔可夫斯基絕對值 (norm)）

時刻、位置是在同一個四維向量之內：X^μ = ( ct, x, y, z )

光速、速度是在同一個四維向量之內：U^μ = ( γc, γv_x,γv_y,γv_z )

能量、動量是在同一個四維向量之內：P^μ = m U^μ= ( γm c,γmv_x,γmv_y,γmv_z) = ( E / c, p_x, p_y,  p_z )

電位、向量位同屬一個四維向量之內：  A^μ = ( Φ/ c, A_x, A_y, A_z )

 

新的動量與能量公式

動量

不再是 p = m v ，而是

p = γ m u

其中 u 是某觀察者看到的速度，而 m 永遠指的是靜止質量。這樣定才能滿足動量相關定律（如動量守恆）在相對論中對所有觀察者定律不變。

Halliday 課本教法如下：需重新定義動量，以使動量守恆定律適用於不同相對速度的觀察者：

p = m × 觀察者座標系中之距離 / 靜止座標系中之時間 = m Δx / Δt₀

（觀念：proper time 才是對應到純量的時間，放在分母的東西必須要是純量）

 

力

力的正確公式是

F = d p / d t 

（不能再用 F = m a，即使有所謂的相對性質量 m_r，也不能直接把 m_r 代入 F = m_r a ，Giancoli 叮嚀）

 

能量

先只考慮動能（位能在此無關），本來是 1/2 m v²，但在相對論下，動量定義已經不同，

能量公式的推導

W = ∫ F dx = ∫ dp/dt dx

其中 dp / dt = d(γm u) / dt = m/[(1 - v²/c²)^(3/2)] dv/dt

（積分過程見課本）

功－功能定理繼續適用，即 ΔK = W ，則得

K = (γ-1) m c²

Bauer & Westfall 課本，是先說明愛因斯坦提出物體靜止時 E₀ = m c²，故加入動能後得

E  = γm c²

上式 E 是相對論下之總能

靜止時 E₀ = m c²，移動時，多了 γ 的係數因子， E = γE₀ ，即 E  = γm c² 。

 

動量－能量關係

非相對論下 E = p² / 2m ，在相對論下

由於 E = γm c² 、p = γm v，而有

E² = p² c² + m² c⁴

請注意這個式子中沒有 γ、β 等相對速度有關的量，上式是一個滿足不變性的方程式。其中

m² c⁴ = E² - p² c² 或 m² = (E / c²)² - (p/c)² 是一個座標轉換不變量。

 

最有名的物理公式

上式 E² = p² c² + m² c⁴ ，在靜止的狀態（或座標系） v = 0 ，故 p = γm v = 0

得 E² = m² c⁴，即

E = m c²

 

2005年，世界物理年

 

另一種推得 E = m c² 的方式

愛因斯坦在尋求獲得相對論之能量（動能）之時，藉由考慮低速下動能應該要重現 1/2 m v² 的結果， 發現必需減去一個常數項 m c² 才可得到，

說明如下：

動能 K = (γ - 1) m c² = m c²/ √[1 - (v/c)2]  - m c²

當 v << c 時， 泰勒展開 γ= 1 + 1/2 β²

驗證：泰勒展開 γ= [1 - β²]^(-1/2)  = 1 + (-1/2) [1 - 0]^(-3/2)  (-1)β² + ... = 1 + 1/2 β² + ...

 

實驗證明

粒子 (μ) 衰變的生命期

高速移動者生命期變長

 

被帶上飛機（繞地球四圈）的原子鐘

的確與地面上的不同

 

其他相對論的證據

beta-射線在磁場中彎折的角度，與質量 (動量) 有關

原子裏的近光速的電子，有效質量 (動量) 要修正

相對論量子力學－電子自旋的發生

廣義相對論

引力與運動的加速等效

空間（時空）受物質彎曲

愛因斯坦方程式

方程式的樣子如下：

G^μν - Λ g^μν = k T^μν

上式的意思是

時空曲率 - 宇宙項 = 物質密度

其中 Λ是宇宙常數、k 是重力常數。裏頭為了營造出恆定宇宙（否則原方程式的解非膨脹即收縮），而設的扺消項。

1929 年在哈伯得到宇宙膨脹的證據時，愛因斯坦自稱這是他一生最大最錯誤。（有數據支持宇宙膨脹是加速之後，有人因此說，難到愛因斯坦的宇宙項終究還是加對了嗎？）

 

黑洞

這是愛因斯坦方程式的一種解，質量密度大得時空彎曲到連光都出不來。

 

宇宙膨脹

這也是愛因斯坦方程式解的的一種解，但注意質量的附近並未膨脹。

 

實驗證明

太陽背後的星光（重力透鏡）（課文開章圖則為銀河系的）

 

水星公轉（近日點、遠日點）的進動

 

相對論在生活科技上若應用

全球衛星定位系統（GPS）

http GPS 1, 2

http 原子鐘

狹義與廣義相對論都有用到

狹義：衛星對地面有速度

廣義：衛星與地面受重力不同

原子鐘之間的同步化是精確到 10^-13，而以衛星速度 4 km/s ，其時間膨脹與否的相對誤差是 10^-10，看雖不大，但比原子 鐘之間的同步能達到的精準度還差一千倍，不作修正將使定位結果大大失準。