電腦模擬:與時間有關的薛丁格方程式 - 波包
參考來源:本節取材自 Gould and Tobochnik 之 An Introduction to Computer Simulation Methods 一書,
程式則由李老師研究群從原來True BASC 語言改寫為 Fortran / PGPLOT 版本
時變性薛丁格方程(波包散射)
時變性的薛丁格方程式比非時變的困難得多,從初始時刻 t = t0 開始,每推進一段微小的時間,就要解出整套波函數在空間中的分佈,更麻煩的是,這樣的多變數的解微方問題容易造成不穩定,根本上破壞了解的正確性。我們在這小節因此要學習很保守很穩定的方法,以便處理非時變性薛丁格方程式的積分求解問題。 (像是參考書提到我們不應採用 (18.17) 式那種方式的演算法,而應採用 (18.18) 那樣的,細節請見原文)
Gould and Tobochnik 書中採用了另一種方法,它是把時變性波函數(一定有實部與虛部)的實部與虛部分開處理,從原本的薛丁格方程式(以下簡化為一維)
i
hd/dt Ψ(x,t) = -h2/(2m) d2/dx2 Ψ(x,t) + V(x) Ψ(x,t)再令
Ψ(x,t) = R(x,t) + i I(x,t)
拆開成兩組分別處理
d/dt R(x,t) = Hop I(x,t)
d/dt I(x,t) = - Hop R(x,t)
如果在這裏使用半步法(中點法),這種演算法本來是要再多算中點斜率猜測值的(修過數值方法的同學可次回想一下階隆巨庫塔法的策略),但在這裏的狀況成了 I(x,t) 是 R(x,t) 的斜率、-R(x,t) 也是 I(x,t) 的斜率,就可以安排成 R(x,t) 永遠在格子點求值,而 I(x,t) 永遠在中間點求值,如此就都不必多花額外的一倍算求中點斜率了,具的的演算法如下:
R( x, t + Δt ) = R( x, t ) + Hop I( x,t + Δt/2 ) Δt
I( x, t + (3/2)Δt ) = I( x, t + Δt/2 ) - Hop R( x, t + Δt ) Δt
在這種方式的表示下,機率密度 P(x,t) = R(x,t)2 +I(x,t)2 仍可以用以下這種方式來表達
P(x,t) = R(x,t)2 + I(x,t- Δt/2) I(x,t+Δt/2)
P(x,t+Δt/2) = R(x,t+Δt) R(x,t) + I(x,t+Δt/2)2
Visscher 證明上述演算法在滿足 -2
h/Δt < V < 2h/Δt - 2h2/(mΔx)2 這樣的 V 與 Δx 值是穩定的 [Ref. Computers in Physics 5(6), 596 (1991)]。
核心演算法提要:
位勢的形式是以定義函式的方法為之。
解微分方程一定需要初始值,初始的波包在此採用會給出常態分佈之機率密度者。其初速、波包大小(寬度)都可以直接在參數中調整。
在此初始值是一個波的空間分佈,採用高斯(即常態分佈)函數,注意波數(又叫波向量)也加進去影響其相位。實部與虛部都需要初始值,它們各自在高斯分佈上有套上 cos 波及 sin 波,波的群速度從那裏引入。本節所採用的演算法,虛部與實部差 1/2 Δt,因此它們的初始值也在不同的時刻定義故虛部就又多一個相位(詳見參考書籍或範例程式)。值得注意的一點是,而其機率分佈看不到動量的物質波波長結構,恰好只呈現光滑的高斯分佈。
請注意這裹有時間、空間兩個變數,都有被離散化,但在此只有時間是需要做微步推進 Δt 的,Hamiltonian 算符中包含了對空間的二次微分,在那裏相鄰近的空間座標格子間的(波)函數值是有一起作些運算,但不同空間的波函數不是從,而是一開始就給了分佈在整個空間(即空間中處處有定義)的波函數作為初始條件。從演算法上來看,x 點上的波函數值永遠是由上一時刻
試問,新時刻處處的波函數分佈是否仍滿足薛丁格方程式,也就是說
我們是先把空間
撰寫程式
等不及了?先偷看一下助教與老師寫的範例程式

在程式內幾個與物理特性有關的參數
x0:起始中心位置
k0:初始波向量(正比於動量,也就是正比於速度)
width:初始 高斯函數(常態分佈) 形之波包的寬度
dx:離散化後的空間間隔
dt:離散化後的時間間隔
V0:位勢高度
a:位井的半寬,但在階梯狀時是位壁的位置
xmax:x 方向的右邊界
xmin:x 方向的左邊界
操作、問題與討論
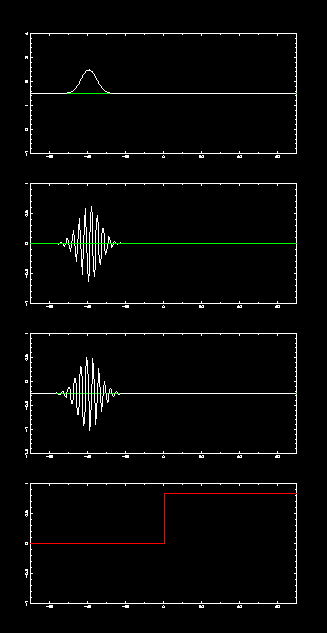
一、平坦位勢中的波包傳播
把位勢高度定為零。
二、射向階梯狀的位勢
觀察透射及反射。
三、透射位壘
改造位勢函數,使其能處理位壘(即平坦區域中間有一高度自定的突出)。
四、在無限深位井內的演進
五、兩個波包迎面對撞(波包對撞機)
請自行加入另一個波包(在波包初始化的副程式中修改),觀察對撞。
自己試試看波包對撞,不成功再參考