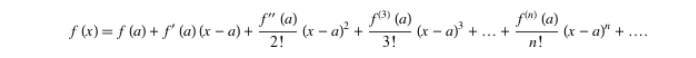
微積分 I
微積分(歷史切入)
最早被稱為是 "流量" 的數學。由英國的牛頓與德國的萊布尼玆在三百多年前所各自提出。
牛頓體會到求切線、求速度、求極值 、甚至是求面積,都出現
( f(x+h) - f(x) ) / h
這樣的型式,想把它整理成公式,以後用起來更加方便。
切線:從圖形直接體會
速度:若把位置當作時間的函數,則如何求瞬間速度?
極值:長度 a 的線段分成兩段作為矩形的兩邊,如何切才使矩形最大?Fermat 的想法,最大時,稍為變動一下,其值不變。具體作法是:假設 f(x) 的極值出現在 x0,則 設 f(x0) = f(x0+h),化簡此式,並把含 h 的項丟掉,可得 x0。
面積:以 y = xp 為例。
註:很好的參考書:康明昌,微積分入門
為什麼需要 δ - ε 方式的定義?
要談連續與極限,都需要講到函數在極鄰近定義域的值。
非常 "接近",代表很小很小的間隔,然而,什麼叫作小?最小能有多小?是 "無限小" 嗎?
由於我們無法處理無限小,因此要迴避使用它,而必須採用下面 δ - ε 的定義方式。
嚴謹基本定義
極限
連續
導數
非標準分析
(允許無限小存在的數學體系)
http://zh.wikipedia.org/zh-tw/非標準分析
泰勒展開式與近似
公式
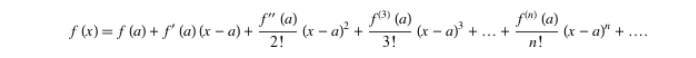
http://mathworld.wolfram.com/TaylorSeries.html
另一種常見的展開表示法:
證明
假設 f(x) = A + B (x-a) + C (x-a)2 + D (x-a)3 + E (x-a)4 + ..... , 微分一次得(這裏有利用到 d/dx xn = n xn-1,證明如下)
f'(x) = B + 2 C (x-a) + 3 D (x-a)2 + 4 E (x-a)3 + ...
f''(x) = 2 C + 2*3 D (x-a) + 3*4 E (x-a)2 + ...
:
於上列恆等式組全代入 x = a,則 :
f(a) = A
f'(a) = B
f''(a) = C / 2
:
得證。
近似
當 | x-a | < 1 時 (x - a)n 越小, 高次項可忽略
以有限的泰勒展開項數來近似一些函數的圖例
http://yll.loxa.edu.tw/0_gsp/taylor/taylor.htm
回家動手做
sin(x) 的泰勒展開作圖(用 fortran 程式及 pgplot 繪圖)
重要基本函數的微分
冪函數或整數冪函數
d/dx xn = n xn-1
證明:用基本定義 d/dx xn = limx->0 (1/Δx) . [ (x+Δx)n - xn ] ,其中 (x+Δx)n 以多項式展開,為 xn + nxn-1Δx + O(Δ2),故
原式 = limx->0 (1/ Δ x) . [ nxn-1Δx + O(Δ2) ] = limx->0 [ nxn-1 + O(Δ) ] = nxn-1 ,得證。
指數函數
d/dx ex = ex
證明: 首先以級數展開 ex = ∑n=0∞ xn/n! (這是一個值得記住的 ex 的定義,連 x 是一個矩陣時都會對)
逐項微分之 ∑n=0∞n xn-1/n! = ∑n=1∞ xn-1/(n-1)! ,發現原公式不變(只要重定 m = n-1),得證。
Euler 最喜歡的公式
eiπ - 1 = 0
這條公式裏有 π、 e、i、乘法單位元素 1,以及加法單位元素 0。
eix = cos x + i sin x
這是有名的 Euler 公式 (西元1748年) 如何發現的可能過程
http://en.wikipedia.org/wiki/Euler%27s_formula
歷史上發展的順序,是先有微積分後才有這個公式。我們這裏所提供的說明,是為了幫助大家容易驗證這些基本函數微分的結果。Euler 所定義的指數與對數是極限的方式:
三角函數
利用 sin x = (eix - e-ix) / 2i 及 cos x = (eix + e-ix) / 2 的關係,可得知
d/dx sin x = cos x
d/dx cos x = sin x
對數函數
d/dx ln x = 1/x
d/dx ln f(x) = f'(x)/f(x)
微分運算
函數乘積的微分,萊布尼茲律
d/dx [f(x)g(x)] = f'(x)g(x) + f(x)g'(x)
可以簡單地由基本定義證明。
合成函數的微分,鏈鎖律 (Chain Rule)
合成函數 f(g(x)) = f。g(x)
f。g' (x) = f'(g(x)) g'(x)
教電腦做微分(求函數斜率)
教電腦做積分(求圖線下面積)
從一維空間、二維空間,到三維空間(向量微積分)
梯度
散度
旋度
格林定理
方程式與微分方程式
何謂方程式(equation)
又叫等式
不同於另一個詞 恆等式 (Identities)
何謂微分方程式(differential equation)
教電腦解微分方程式(奧伊勒演算法及一些高階演算法)
微分方程式與物理定律
我們學物理的目的(解決真實世界中的問題、預測自然與宇宙萬物的現象)
牛頓的運動方程式
波動方程式
流體力學的伯努力方程式
電磁學的馬克斯威爾方程式
薛丁格方程式
迪拉克方程式
愛因斯坦的時空與質量方程式