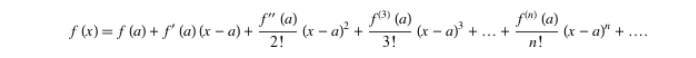高二數學下與近代物理
一、寫下通過空間中任意兩點 (x1,y1) 與 (x2,y2) 的那條直線之方程式。(5%)
(y - y1) / (x - x1) = (y2 - y1) / (x2 -x1) 或其整理後的形式。
二、三個向量之分量表法的行列式值具有什麼意義?若其為零又代表什麼意思?(10%)
代表由該三個向量所張開成的平行六面體之體積。其值為零則代表三向量共面(或四各線性相依)。
三、證明平面的 R = ma + nb 的格子點不可能有五重旋轉對稱(其中 a、b 為向量,m、n 為整數)。(5%)
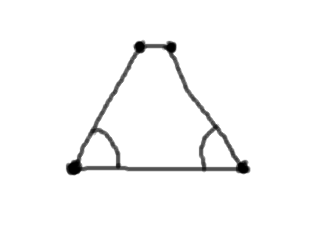
在所有的格子點中找出兩個最接近的,在不失一般性的情況下,一左一右,拉一條向量,這會是最短可能的週期向量。再來,各自針對兩個點作 2π/n 的正負方向轉動,左手邊的點轉 2π/5, 右手邊的點轉 -2π/5,如此與原先的兩點連線形成一個梯形,這個梯形的斜邊長等於底部長(因為斜邊的點是轉動得到的),至於平行於底邊那個新連線,它的長度是兩個 | a | cos(2π/n) 的和,這個長度要是比 | a | 短,就是矛盾了。現在我們注意 cos(x) 在第一象限是一個遞減函數,角度從 0 到 90 度其函數值從 1 遞減到 0。它在 90 度時才會使梯形的頂邊長等於底邊長,此時為 2π/n 的 n=4;而在 60 度時兩點重合,梯形成為正三角形,此時為 2π/n 之 n=6。對於 n=5 而言,頂邊的長度不為零且又比底邊短,故矛盾。
四、從基底的角度出發,試比較向量空間與函數空間之相似性。 (10%)
任何向量皆可以由一組線性獨立的基底展開,為了方便我們喜被用正交(即內積為零)的基底向量,如此任何向量都可以用其投影(內積)到各基底向量的係數組來表示,我們通常稱之作向量的分量,有下列關係或形式:
V = Vx ex + Vy ey + Vz ez
其中 Vx = V. ex
函數之間也可以定義內積,就是相乘(有複數的則是共軛相乘)後積分,等於零的情況也叫做正交,如此,一組兩兩之間互為正交的函數可以被拿來當作基底,任意函數對一組正交函數分別作內積後,則得展開式中對應項的各係數。如此任意函數可由基底函數展開與表示,如同向量空間那樣。
由於函數空間的維度是無限維,因此想要精確地、無近似地用基底函數配合投影(內積)的係數展開任意函數,則需要無限多個基底函數。所幸,在實用的場合,只需取有限個基底就非常精確了。例如有名的富利葉級數展開即是如此。
五、這是近視(交叉)立體對圖。數一數,晶胞裏頭有幾顆原子?(頂角算 1/8 顆、邊上算 1/4 顆,面上算 1/2 顆)(5%)
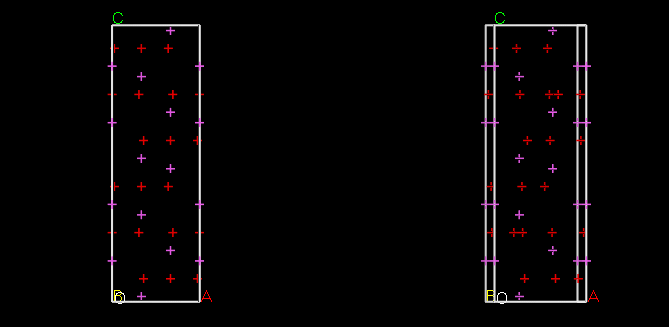
共 30 顆(粉紅 10 顆、紅色 10 顆)。
六、函數 f(x) 在 x = x0 處連續,試用 δ- ε 數學語言說明之。(10%)
對任何 ε> 0,存在 δ> 0,使得 所有滿足 | x - x0 | < δ之 x,其 | f(x) - f(x0) | < ε
七、己知一函數 f(x) 可作 (x-a)n 之級數展開,試證明其形式為泰勒展開式 (10%)
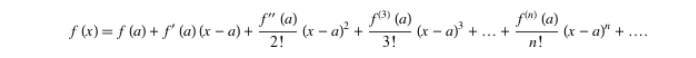
假設 f(x) = A + B (x-a) + C (x-a)2 + D (x-a)3 + E (x-a)4 + ..... , 微分一次得(這裏有利用到 d/dx xn = n xn-1)
f'(x) = B + 2 C (x-a) + 3 D (x-a)2 + 4 E (x-a)3 + ...
f''(x) = 2 C + 2*3 D (x-a) + 3*4 E (x-a)2 + ...
:
於上列恆等式組全代入 x = a,則 :
f(a) = A
f'(a) = B
f''(a) = C / 2
:
得證。
八、己知待求函數 y(x) 之斜率函數為 f(x,y),即 dy/dx = f(x,y) ,請問電腦數值運算如何求解 y(x) ?(10%)
使用 Euler 演算法或其改良方法,寫下第 n 步與第 n+1 步的關係,例如下式:
yn+1 = yn + f(xn,yn) Δx
只要有某個己知的初始值 y0,上述演算法就可以獲得所有的 yn,當然,Δx 要夠小才正確。
九、是誰解釋了黑體幅射現象?其推想過程與結果是如何?(5%)
普朗克。古典理論無法解釋物體受熱所散發出來的電磁波其能量與頻率的分佈關係,但那是基於很成功的能量均分統計分佈所預放出來的。經過多年的嘗試,普朗克發現如果它把電磁波駐波振幅的能量當作不連續,且其基本單位的大小正比於頻率則他的預測光譜形狀就與實驗完全吻合。他進一步由實驗所測量到的能譜(光譜)分佈比對而定出單元能量與頻率的比例常數,這就是影響量子革命的普朗克常數。
十、2009 年諾貝爾物獎頒給那兩種發明的貢獻者?(5%)
光纖 與 電荷耦合裝置(CCD)。
十一、與時間無關的薛丁格方程式,為什麼會與時間無關?(5%)
當問題中的位勢與間無關時,則原方程式透過分離變數的技術,簡化成一個只有空間座標的方程式與一個只有時間座標的方程式。而原方程式的解則是兩個新方程式個別解的乘積。時間的部分僅剩極單純的的形式(解的形式皆固定),而空間部分才是主要待解的目標,它的解與時間無關。
十二、什麼樣的實驗驗證了原子的結構較行合核桃模型而非西瓜模型?(5%)
拉塞福的氦核束射向金箔實驗中看到,除了不偏折散射與較少的小角度偏折散射之外,尚有少數幾乎原路折回的大角度反彈,代表原子之質量集中於一點。
十三、物質波的觀念由誰提出?其波長如何計算?(5%)
德布洛利,λ = h/p (波長 = 普朗克常數 / 動量)。
十四、束縛態電腦模擬計算中,怎樣的能量猜測值才是解?為什麼?(10%)
能夠使波函數在所有的範圍(或越大越好的範圍內)不發散無限大或無限負的能量值。
求解微分方程式的演算法不論如何都是一直可以進行下去的,然而波函數存在之空間中的總機率密度為 1,如果數值解越向外越發散,則那個解在束縛區不會有出現的機率(而是出現在不切實際的無窮遠處),因此就不是解。反之,只有在整個空間範圍都不發散的,才是束縛態量子問題的解。