咖啡冷卻問題
問題
假設剛沖好的咖啡是攝氏 80 度、適合飲用的溫度是攝氏 45 度，又假設加入奶精後咖啡固定會降 5 度。問應該先加奶精還是後加奶精才會比較早喝得到咖啡？
物理量
溫度 T、時間 t ，我們希望知道 T(t) ，以便知道在某特定定 t1 時的溫度。
數學模型（物理公式：牛頓冷卻定律）
dT / dt = - r (T - Ts)
其中 T 是咖啡溫度、 Ts 是室內（空氣）溫度、 t 是時間，以及 r 則是冷卻係數，可視為一個常數。
建立咖啡之冷卻係數的方法，從以下實驗的表：
以下為實測值，當時室溫 17 度 C：
時刻（分鐘） 黑咖啡溫度(度C) 白咖啡溫度(度C) 0 82.3 68.8 2 78.5 64.8 4 74.3 62.1 6 70.7 59.9 8 67.6 57.7 10 65.0 55.9 12 62.5 53.9 14 60.1 52.3 16 58.1 50.8 18 56.1 49.5 20 53.3 48.1 22 52.8 46.8 24 51.2 45.9 26 49.9 44.8 28 48.6 43.7 30 47.2 42.6 32 46.1 41.7 34 45.0 40.8 36 43.9 39.9 38 43.0 39.3 40 41.9 38.6 42 41.0 37.7 44 40.1 37.0 46 39.5 36.4
演算法及程式
一階微分方程式的程式
最一般形式的一階微分方程式，是如下的形式：
dy/dx = f(x,y)
其中 f(x,y) 可次是任何以 x, y 為自變數的顯函數。在微分方程式的問題中，f(x,y) 為所給定的已知，而 y(x) 則是未知且希望求得的解。
我們要如何求解 y(x) ？
Euler （奧依勒）演算法
在 Δx → 0 的情形下Δy/Δx = dy/dx = f(x,y)，也就是說Δy = f(x,y)Δx。
把 x 分成許多等間隔的小單位，即Δy ≡ yn+1 -yn、Δx ≡ xn+1 - xn，則上式成為
yn+1 - yn = f(xn,yn)Δx，也就是說
yn+1 = yn + f(xn,yn)Δx
上式就是 Euler 演算法，它告訴我們只要知道第 n 格的 y(x) 值 yn，就可以算得下一格的 y(x) 值 yn+1， 故只要知道 y(x) 在某個 x0 處的起始值 y(x0)
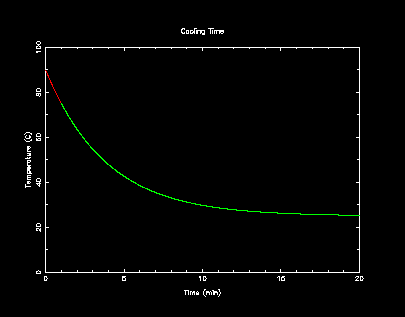
程式流程：給定冷卻係數、咖啡初始溫度、室溫，畫出 T(t) 的圖
(0) 開始
(1) 讀入冷卻係數、咖啡初始溫度、室溫、小間隔時間設定、希望模擬之時間
(2) 在迴圈中，以 Euler 法預測下一小段時間後的溫度，並畫圖，直到迴圈跑完
註：核心結構如下：
T = T_initial
do i = 1, 10000
T = T - r * (T - Ts) * dt
end do
(3) 結束
請自行撰寫程式
寫好程式後編譯時，由於你的程式中有使用到 pgplot 繪圖副程式，因此編譯指令要像這樣下：
gfortran -o my_prog.x my_prog.f -L /usr/local/pgplot -lpgplot -lX11
注意以上的 X 是大寫、11 是數字、有 -L 的地方一定要用大寫，後面連結程式庫用的 -lX11 與 -lpgplot 之 "-l" 則是英文小寫 l 。
完成圖例
範例程式參考
等不及了，先玩一下老師己經做好了的可執行檔 cooling.x
一下子寫不出來，偷看一下老師範例程式中的寫法 cooling.f
（儘量先自己試試看，注意可執行檔是 Linux 環境用的）
新增：純文字極簡版
再加入繪圖功能
系列習題：
一、依照牛頓冷卻定律，寫一個預測物體溫度 T(t) 的程式，其中冷卻係數 r、初始溫度 T(0)、環境溫度 Ts，以及微小時間間隔Δt 由外部讀入。
A. 你的程式寫好了，也順利地通過編譯並產生一個可執行檔，也就是指令的語法都正確了，但你怎麼知道它有沒有邏輯上的錯誤（程式內部的錯誤通常叫 bug，因為歷史上曾有蟲子卡在真空管燒掉導致電路借邏輯錯誤的事件）），或比方說不小心把 + 號打成 - 號？
B. 微小時間間隔Δt 是程式使用者自己必須決定的量，請試試看不同數量級的大小。你覺得用多小的值才夠精確？
注意：如果Δt 用得太大，除了答案很不精確之外，更有可能導致咖啡溫度比環境溫度還低的不合理情況。（看看公式，試著想像一個很大的Δt 值會導致什麼結果？）
二、從實驗數據（參考下表）建立咖啡之冷卻係數的實作
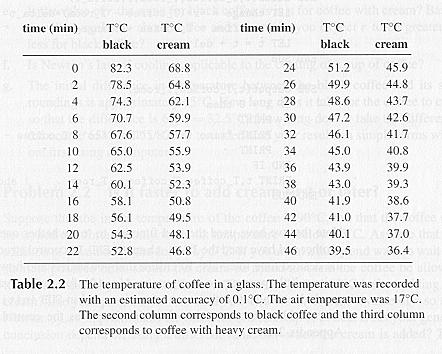
Ａ．你認為牛頓冷卻定律能不能描述上述的實況？（想想看我們要怎麼樣來回答這個問題。）
Ｂ．如果我們願意接受用牛頓冷卻定律為模型來描述實況中的冷卻過程，則你要怎麼樣獲得一個較符合的冷卻係數 r 值？
自己先想一想，如何定出 r 值（想不出來再看）
三、假設加入奶精只會簡單地把瓶中溫度降低攝氏五度，則問一瓶剛沖好攝氏 90 度的咖啡，要想快點達到開始可以品嚐的攝氏 45 度，你建議先加奶精或是後加奶精？
四、一個量的變化率與當時該量之大小有關的現象，還有什麼例子？（核衰變）
五、演算法的精確度與穩定性的問題。（原參考教科書內文）
利用電腦進行數值運算，其誤差的來源有二，其中一個是四捨五入誤差（又叫捨去誤差或捨入誤差，英文叫 round-off error 或 rounding error，它是發生在當電腦在利用其有限的位元處理有小數點的數值（如實數，又叫浮點數）傯會有需要四捨五入的情況，比方說若僅保留小數點後一位，則 1.1 乘以 1.1 的結果就要表示成 1.2 而不是更正確的 1.21，；另外一種誤差是來自演算法裏頭所使用的近似，叫截斷誤差或修剪誤差，英文叫做 truncation error，會有這種名稱是因為演算法常用無窮級數展開的形式，其中很有名的比方說泰勒展開式（Tylar's expansion）。
額外例題：
進階閱讀：
Gould and Tobochnik, An Introduction to Computer Simulation Methods -- Applications to Physical Systems, Addison Wesley (1996) Chapter 2
