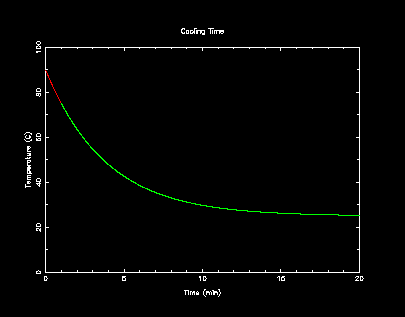
問題:先加奶精或是後加奶精咖啡冷得快?
物體量:溫度隨時間的變化
物理定律(數學模型):牛頓冷卻定律(溫度變化率與溫差呈正比)
dT / dt = - r (T - Ts)
其中溫度 T 是時間 t 的函數,即 T(t) ,Ts 是外在環境的溫度(室溫),
冷卻係數 r 如何定出? (實作題,第二題)
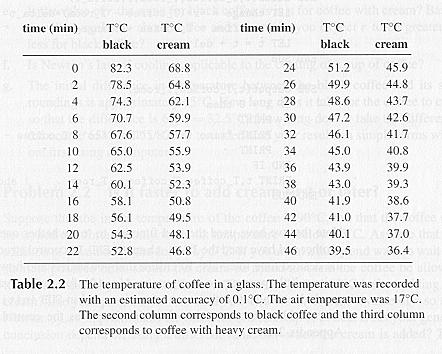
以下為實測值,當時室溫 17 度 C:
時刻(分鐘) 黑咖啡溫度(度C) 白咖啡溫度(度C) 0 82.3 68.8 2 78.5 64.8 4 74.3 62.1 6 70.7 59.9 8 67.6 57.7 10 65.0 55.9 12 62.5 53.9 14 60.1 52.3 16 58.1 50.8 18 56.1 49.5 20 53.3 48.1 22 52.8 46.8 24 51.2 45.9 26 49.9 44.8 28 48.6 43.7 30 47.2 42.6 32 46.1 41.7 34 45.0 40.8 36 43.9 39.9 38 43.0 39.3 40 41.9 38.6 42 41.0 37.7 44 40.1 37.0 46 39.5 36.4 白咖啡與黑咖啡是否都滿足牛頓冷卻定律所描述的呢?如何確認?如何做下一步?
演算法:
這裏數學問題的本質問題:
我們只知道函數 y(x) 的處處斜率 y'(x) 是等於已知的 f(x),(f(x) 中若明顯出現 y,則也可以寫成 f(x,y) ) 。而我們希望知道函數 y(x) 。
Eular 演算法:觀點一(把斜率離散化)
若 dx 很小,原函數 y(x) 在 x0 處的斜率值 f(x0) 是相當於(白板作圖示範):
[ y(x0+dx) - y(x0-dx) ] / 2dx0,也可寫作
[ y(x0+dx) - y(x) ] / dx (反正 dx 很小)
,因此
y(x0+dx) = y(x0) + f(x0) dx
如果我們定一格 xn 到下一格 xn+1 之間的間格是 dx ,則上式變成
y(xn+1) = y(xn) + f(xn) dx
而這正是 Eular 演算法,告訴我們如何從斜率函數一步步推出原函數。 (但也請大家注意,起始的第一個點的函數值必須要先知道。)
Euler 演算法:觀點二(把微分符號近似換成差分符號,適合已經讀過微積分的童學)
對於一個簡單的微分方程 dy / dx = f(x,y),在 Dx 很小時可當作 Dy / Dx = f(x,y),故 Dy = f(x,y) Dx
又當 Dx 是等間隔 xn - xn-1 = ... = x3 -x2 = x2 -x1 = Dx 時
Dy = yn+1 - yn = f(xn,yn) Dx
這裏的
yn+1 = yn - f(xn,yn) Dx
就是有名的 Euler(奧依勒,也有翻譯作歐樂)演算法。
程式流程:給定冷卻係數、咖啡初始溫度、室溫,畫出 T(t) 的圖
(0) 開始
(1) 讀入冷卻係數、咖啡初始溫度、室溫、小間隔時間設定、希望模擬之時間
(2) 在迴圈中,以 Euler 法預測下一小段時間後的溫度,並畫圖,直到迴圈跑完
(3) 結束
請自行撰寫程式
寫好程式後編譯時,由於你的程式中有使用到 pgplot 繪圖副程式,因此編譯指令要像這樣下:
gfortran -o my_prog.x my_prog.f -L /usr/X11R6/lib -lX11 -L /usr/local/pgplot -lpgplot
以上注意 X11R6 的 X 與 R 是大寫、11 跟 6 一樣是數字、有 -L 的地方一定要用大寫,後面連結程式庫用的 -lX11 與 -lpgplot 之 "-l" 則是英文小寫 l 。
完成圖例
範例程式參考
等不及了,先玩一下老師己經做好了的可執行檔 cooling.x
一下子寫不出來,偷看一下老師範例程式中的寫法 cooling.f
(儘量先自己試試看,注意可執行檔是 Linux 環境用的)