雙點邊界值問題：射擊至中點法

射擊至中點法

在有一些場合，若上一個單元那種從一邊射擊至另一法的方法並不是很好，例如：

(1) 初始值很不容易到達目標點，甚至是發散或程式中斷，積分根本做不完，也就無從進行下一步是否命中的判定了。

另外有一種可能，是：

(2) 邊界點本身此較特殊（例如剛好那一點是奇異點，真要描述就要使用漸近形式 asymptotic form），求解的步調逐漸向它逼近會產生問題；反之，若是由該點出發向外延伸就沒有這個問題。

以上這兩類問題，一個是發生在中途積分的途徑上（太遠則初始值不好預測），另一個是發生在終點上（行為奇異），我們就可以使用射擊至中點來改善以上的狀況。

其實，射擊至中點法的基本精神與作法跟射擊法是一樣的。只不過現在是從兩側射向中間，兩側都要對不足的初始條件作猜測。分別完成各自的射擊至中點（中間某一點，不一定必須是正中央），至於解題是否達成的判定，則視來向兩側的射擊給果函數值 yi 是否在中點點上合而為一，若尚未達成，則上層的全域收斂牛頓法會試著用找根的策略來預測下一步更好的猜測初始值，如此反覆進行直到求解成功為止。

副程式的使用

shootf 是本節的主要副程式，但注意它並不是主程式所呼叫的第一個副程式，這裏的情形與上一節的 shoot 一樣，主程式先呼叫 newt，newt 內的 funcv 才是這裏的 shootf。使用起來幾乎是和上個單元的 shoot 是一模一樣的。

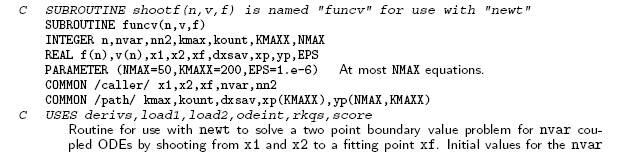
所需的主程式的架構與使用者必須提供的 derivs 、load、score 等，只不過 load 與 score 都各需要兩個，在這裏事實上 shootf 自行會把 f1 與 f2 相減定成 f 來給 newt 求根，因此 score1 與 score2 裏面直正要做的事情也就只有各自把 y 指定給 f1及 f2 而已。

主程式需要讀入 V1(n2) 及 V2(n1) 兩組分別給兩邊用的初始猜測值（其中 n1 + n2 = nvar）。這裏有一個新的指令要學，就是 equivalence，它是要用在主程式中，課本副程式的說明提醒我們要寫成

equivalence (v1(1),v(1)) , (v2(1),v(n2+1))

這樣就可以把 v1(n2) 與 v2(n1) 一起排入 v(nvar) 陣列之中了。

另有一個實作上的點需要考慮，就是中間貯存結果如何取得的問題，由於 odeint 在 funcv (shootf) 中連續被呼叫了兩次，第一次的資料是會被蓋掉的。有不同的方法可以解決此一問題，其中一種，就是在求解完成後利用最後的 v(nvar)，即 v1(n2) 與 v2(n1) ，分兩次去去呼叫 odeint，叫完一次就畫一組圖。（大家不要忘記，odeint 的 x 範圍端點 x1、x2 順序是可以反過來的。）為了做到這一點，我們就要參考 odeint 在 funcv 中被叫用的方式來在主程式的最後多執行 odeint 一遍，如此來獲得繪圖或分析答案所需要的中間結果。