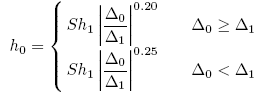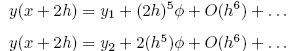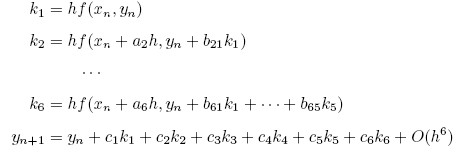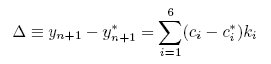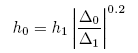R-K 方法在前一個單元己經介紹過,使用微步副程式 rk4,它搭配 rkdumb 這個每一個微步都等間隔的積分驅動器副程式,提供了直接有效的求解方案。
然而,我們不難想像,在推進微步的求解過程中,各階斜率函數的變化快慢在各處不盡相同,若以同樣的步幅寬度來推進,則可能有些地方精確度不足,而有些地方則又細分了太多不必要的區間,這並不是效率最高的方法。
如果積分驅動器副程式能監控每一步的誤差,並作妥善的調適以符合使用者所設定的設差容忍度,則函數變化起伏越大的地方才會用到越小步幅的,有助於整體效率的大幅提昇。這種方法,我們稱之為具步幅調適控制功能(Adapted Step-size Control)的方法。
在本節(NR 16.2) 中課本介紹有誤差控制的 R-K 演算法,並推薦為可用於多種不同類型常微分方程式的求解的泛用工具,尤其是在下一章介紹兩點邊界值問題(NR 17.1、17.2)時也會用到,因此找我們仍要認識並練習使用這個方法。
步幅調適的基本觀念,在於 (1) 能監控誤差大小 (2) 能依誤差大小調整出最適切的步幅。
在此演算法設計的技巧高於基本的數學觀念,本單元我也就不要求大家一定要熟悉其公式推導上的細節,僅鼓勵有興趣之同學自行深入閱讀下列講義及原課文。至於副程式的使用我們則要求同學們都還是要會,因此會作詳細的分析說明。
不管如何,在此將演算法設計的要點(接課文順序)詳述如下:
(1) 誤差估算的方式
一種常用的方法(但不是本節副程式所採用的),是在原演算法的推導式中把步數加倍(即步幅減半),而步數加倍情況下走兩步等效於原演算法走一步,但它們的泰勒展開形式並不全同因此有所差異,
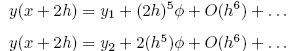
利用此一差異可次得出原演算法內在的誤差行為(以正比於步幅大小的幾次方這種方式呈現)。
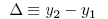
課文公式 (16.2.1) 至 (16.2.3) 就是在說明推導細節,是蠻普遍的作法。有加走步數倍增之方法的函數求值動作裏,有些是先前走一步就做過的,見圖
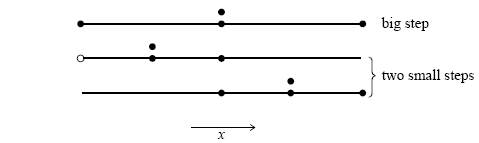
因此總共是 11 次,比起一開始就用一半步幅大小的 8 次(在相同立足點上來比,要兩次半步才相當於推步一步的範圍),代價是 1.375 倍,不算太多,而所換得的是估計的誤差資訊,事實上會獲得相當大的效能提昇。
以上的作法,看起來雖然可以繼續再進一步組合出更高階的演算法,
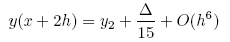
但已有相當高階方法可用的情況下,這未必是解決問題所最需要的(更高階不一定代表更精密),這樣作並不能給出我們最需要的,就是誤差估計。
課本裏面也順便提到為什麼 4 階 R-K 方法是最被廣為採用的,更高階的 R-K 方法也有被推導出來,大家發現只要是階數 M 大於 4 的,都需要多於 M 次的斜率函數求值(但不會多於 M+2 次),因此,對於僅需求值 4 次的 4 階 R-K 方法似乎是比其他階數更划算(課文作者再次提醒大家越高階未必越精準)。
在本節副程式所要用到的,則是針對 R-K,有另一種可行的方式,它是從一個需作六次函數求值的五階的 R-K 方法出發,
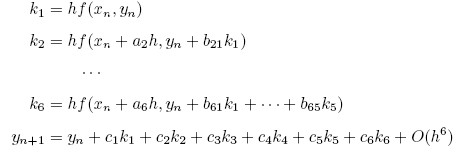
它有另一式特殊組合可形成四階方法,
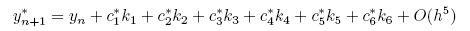
這兩者的差異也就提供了誤差的定義(換句話說,就是表示出步幅大小(x 的誤差)與函數誤差(y 的誤差)間的關係,如下式:
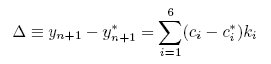
這其中的係數都已經是有人推導完成的確定值,如下表

(2) 調整步幅的策略
前面已提到,誤差估計很重要的一點是,待求解函數 y 的誤差 D 與步幅大小 h 的關係是怎麼樣?
前面的推導看得出 D 是與 h5 成正比,但連接兩者的比例常數我們當然是不知道。 現在讓我們想像使用了 h1 而導致了誤差正比於 D1, 而我們原本若是取了 h0 而造成了 D0,則 h1 與 h0 的關係就會是
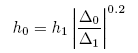
我們習慣上將 D0當作是使用者預先設定好的誤差容忍度,則上面這個關係式有兩種用法:其一、當我們現在這一步用的 h1 獲得的 D1 比 D0 大,我們知道把比例開五次方乘上原來使用的步幅來重跑;其二、如果這一步 h1 估出來的 D1 比 D0 小,則上式告訴我們下一步的 h2 大概可以放大到多大仍是安全的。
接下來的問題,是 D0 本身應該怎麼設定?(請注意, D0 是一個向量,視問題的需要,它對於每一個 yi 都可以有獨立的值的。) 我們前面說要把它當作是誤差容忍值,給一個絕對數當然是一種方法,但是很多時候,我們對問題精確度的要求是相對於函數當時的值,因此若設成是某個很小的數乘上 yi 的大小 eyi,也是很合理。然而,如果這個函數是會振盪變化而通過零,我們也可能希望它是設定為是 e 乘上 y 之最大值的絕對值,也是合理的考量。實際上寫成程式時,可以有一行是設成
D0 = eps * yscal(i)
如果 y 相對的相對大小是重要的,就把每一微步的初始 y 值傳入成 yscal,若是要用絕對容忍值,則改傳入所要定的數值。在課本所附的副程式中,甚至多加了與斜率乘上步幅有關的項,而把 yscal(x) 設成為 |y(x)| + |h*dydx(x)|,之所以會有第二項的形式,是因為我門也會想監控每一微步下函數的變化量。(這其中的諸多考量,可參見課文的進一步細節。)
但是,D0 出現了 h 的一次正比關係會影響到前面開五次方的分析,所幸四次方或五次方並不是那麼不同,課本作者基於實作經驗建議了下次通用的判斷機制,基本上的想法就是,當步幅需要放大(現有步幅太保守),用小一點的開方值;當步幅需要縮小(現有步幅太激進),用大一點的次方值
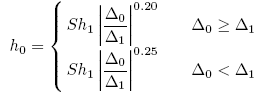
其中 S 是一個略小於 1 的常數。
調適步幅控制的 R-K 方法由下列一組三個副程式達成,其功能略述如下(再次強調,大家要學會自行閱讀副程式的英文使用說明,你自已要能看得出下列要點整理所列舉的事項),
odeint:驅動器(driver)副程式,會問自變數範圍、初始值、精度控制相關條件,以及提供 common block 讓主程式有放答案的地方。
rkqs:"品質管制"。監控每個微步的截斷誤差(trancation error)並且調整步幅 。被 odeint 呼叫,自已再呼叫 rkck。
rkck:能進行五階 R-K 運算的微步的推進,並包含內嵌(embeded)4 階 R-K 以供作誤差監控。
使用者自行須提供的 derivs 副程式會被 odeint (為了作步幅控制) 以及被 rkck (為了推進一微步)兩個副程式所呼叫。
以下是它們各自的細節:
rkqs

需要使用者提供的 derivs 與下面的 rkck ,它是被 odeint 呼叫,自已再呼叫 rkck,主程式需作宣告的東西沒有必須參考這裏的,可當作黑盒子。
rkck

這是最底層的微步副程式,具備算出誤差估計的功能,雖然有直接叫用到 derivs,但這用法與 odeint 處一樣,使用者寫的主程式並不需要與這個 rkck 銜接,也不需要參考這裏頭的變數宣告,可當作黑盒子。
odeint
使用者所寫的主程式,必須直接叫用 odeint, 因此有多處宣告上的細節必須參考,才能把主副程式銜接起來。至於 derivs 則是相當標準單純,與上個單元在 rkdumb 的作法完全一樣。
這個 odeint 是 rkqs 的 driver 程式,會把 x1 ~ x2 範圍內的函數 y(x) 做出來,xn 與 yn 的數值答案是放在公共區塊 /path/ 的 xp 與 yp 中,因此主程式也需要作對應的宣告才能把它拿出來。
閱讀 odeint 的說明區塊,我們可以知道為了使用這個副程式,使用者必須在主程式中以 parameter 方式定義 nvar,並且要輸入 ystart(i)、x1、x2、eps、h1、hmin 這些量傳給 odeint。


使用 odeint 有另一個值得注意的點,就是它是設計為得到最終值 y(x2) 為主,此副程式雖然有提供中間過程的值,但由於步幅大小不固定,因此中間過程的點不是很適合作圖用(不像是 rkdumb 那樣)。它內部仍然有設置公共區塊來諸存中間過程,總共存多少點是由 kmax 與 dxsav 來決定,使用者要自何設定就兩個值,如同上面節錄之程式說明所示。
如果我們想從 odeint 的結果取得其公共區塊裏的中間過程來作圖或看步幅變化的狀況,則善用 common block 中之 kount 是很重要的,它代表了中間值的點數。(xp(i) 在 i 大於 kount 之後都是被設成零,請小心。)
kmax 與 dxsav 具體的意義,則是在課文中交待(還是希望大家要試著學會看懂它)。基本上是說,間隔步幅大於 dxsav 的才會存下來,並且先存到 kmax 用滿為止,兩者固然都是使用者自行設定,但 kmax 最多不能大過宣告的陣列大小 KMAXX 。

c
c This program is written by Prof. Ming-Hsien Lee for demonstrating the use
c of Numerical Recie subroutine ODEINT, RKQS, and RKCK to perform Adaptive
c Step-size Control Runge-Kutta algorithm for solving ordinary differential
c equations. Provided to year 2007 Numerical Methods class.
c
program odeint_main
implicit none
integer nvar,i,nok,nbad
parameter (nvar=2)
real ystart(nvar),x1,x2,eps,h1,hmin
c For common block
integer KMAXX,NMAX,kmax,kount
parameter (KMAXX=200,NMAX=50)
real xp(KMAXX),yp(NMAX,KMAXX),dxsav
common /path/ kmax,kount,dxsav,xp,yp
c For pgplot
integer pgopen,icount,j
real y_min(nvar),y_max(nvar),yy(KMAXX),y_extra
external rkqs,derivs
kmax = KMAXX
dxsav = 0.001
write(*,*) 'What is the beginning and endding of x, x1 ; x2 ?'
read (*,*) x1,x2
write(*,*) 'Input inital vector of yi at x1:'
read (*,*) (ystart(i),i=1,nvar)
write(*,*) 'What is the accuracy eps and first setp size h1 ?'
read (*,*) eps, h1
write(*,*) 'Minimum allowed step size (can be zero) hmin is:'
read (*,*) hmin
call odeint(ystart,nvar,x1,x2,eps,h1,hmin,nok,nbad,derivs,rkqs)
write(*,*) 'Subroutine odeint completed.'
write(*,*) 'Final value of y_i are:'
write(*,*) (ystart(i),i=1,nvar)
write(*,*) 'nok is',nok,' nbad is',nbad
write(*,*) 'The total number of points for plotting is :',kount
c Find Max and min values of yi(x), but here we will use only y1(x).
do i=1,nvar
y_max(i)= yp(i,1)
y_min(i)= yp(i,1)
end do
do i=1,nvar
do j=1,kount
if (yp(i,j).gt.y_max(i)) y_max(i)=yp(i,j)
if (yp(i,j).lt.y_min(i)) y_min(i)=yp(i,j)
end do
end do
c Copy y(1,1:nstep) to yy(1:nstep) for PGLINE plotting
do i=1,kount
yy(i) = yp(1,i)
end do
c Intermidiate reult check
c do i=1,kount
c write(*,200) i,xp(i),i, yy(i)
c 200 format(1x,'x(',i3,') is ',f5.2,' y(',i3,') is ',f5.2)
c end do
c Start plotting
y_extra = 0.1*(y_max(1)-y_min(1))
if (pgopen('/xwin').le.0) stop
call pgpap(6.0,0.75)
call pgenv (x1,x2,y_min(1)-y_extra,y_max(1)+y_extra,0,0)
call pgline(kount,xp,yy)
call pgsci(2)
call pgpt(kount,xp,yy,9)
call pgclos
end
subroutine derivs(x,y,dydx)
real x,y(2),dydx(2)
dydx(1) = y(2)
dydx(2) = -y(1)
end
c subroutine derivs(x,y,dydx)
c real x,y,dydx
c dydx = 2*x
c end
註:上例的題目是 y"(x) + y(x) = 0,而 comment 掉的另一個例題則是 y'(x) = 2x。