三度空間的插值法

二度空間插值法

bi-linear （見課文）

三度空間插值法

四面體法 (Tedrahedron Method)

線性插值函數 f(x,y,z) = a + b x + c y + d z ，具有四個項的簡單形式，其中 a, b, c, d 是待之函數，這需要四個條件來確定。這四個條件恰好由四個頂點的己知表列值來滿足，

vi = f(xi, yi, zi), i = 1,2,3,4

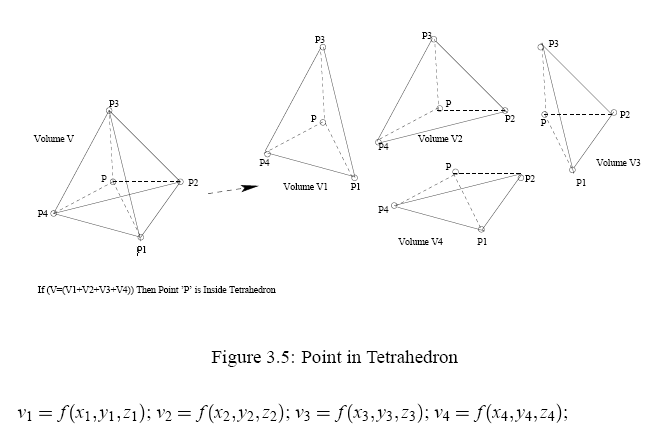
如下圖所示

問題：如何知道給定的插值點 (x, y, z) 是落在那一個四面體之內？

根據上圖，分別算出插值點與四面體的四個面所形成的體積，如果這四個體積加起來等於原四面體的體積，則（從直觀的圖像我們自已可以想想看）這個點就一定落在四面體之內。

問題：三角形與其平面外一點所形成的四面體之體積要怎麼求？（是向量三重積還是行列式值比較接近我們所要的？）

（先問，三角形的面積如何求得？也是基於底乘以高嗎？三角形面積公式彙集 是 1/2 的底乘以高。再問，三維空間中的向量三重積與之結果與 3x3 矩陣的行列式值有沒有一樣？）最後問，任意三角錐的公式為何？1/3 底面積乘以高。請注意，其中底面積是 1/2 底乘以高，因此 1/(3!) 三向量正交乘積。最後問，三向量所張開之三角錐體積是否等於其平行六面體體積的六分之一？