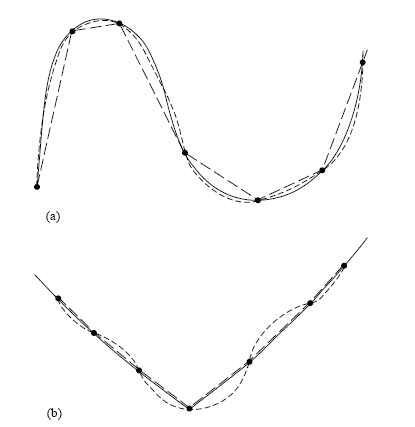
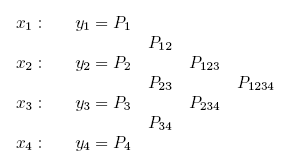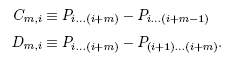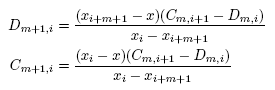大家都知道兩點唯一決定一條直線(不轉彎)、三點唯一決定一條二次曲線(會轉一次彎)、四點唯一決定一條三次曲線(會轉兩次彎,有反曲點),等等。這些曲線都是以多項式的形式(變數出現時,些是整數次方)。
一個 n - 1 次曲線的多項式雖有像 y = a(n-1)x(n-1) + a(n-2)x(n-2) + .... + a1x +a0 這樣的通式可以表示出,但必須代入 n 個表列值才能定出 an-1 至 a0 那 n 個係數,一下子不易看出。
數學上有一個 Lagrange 多項式公式,它可以由 n 對 (x,y) 值唯一決定 n-1 階多項式,且公式非常好記, 如課文中的式 (3.1.1)

記法參考:寫下每一項都有係數 yi,分母全是 (xi - xj),其中 i ≠ j,分子則全部都是 (x - xj),一樣是 i ≠ j ,這樣的項共有 N 個相加。我們的式子最高項次一定是 xN-1,符合 (x - xj) 連乘,並且當 x 恰為某一個 tabulated point xi 時,yi 會因分子分母一模一樣抵消成 1 而留下來,而其他具 yj 的項則因其分子必定有 (x - xi) 而成為零,因此 y = yi,符合表列值的定義。
有了上面 Lagrange polynomial 的定義,拿來寫個程式,對任給的 x 求插值,也並非不可以,只是這樣就少了誤差分析及精密度控制的動作。
真正有用的演算法,是 Neville's 演算法。它定出 Pi 為原本表列值 yi,而 Pi(i+1) 則代表一般表列點是 xi 與 xi+1 所構成的一階 Lagrange 多項式。
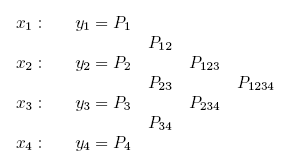
Neville's algorithm 厲害的地方,是發現由低階多項式,可以經由組合而系統化地得出更高階多項式(例如自 P12 及 P23 得出 P123),根據下列關係式:
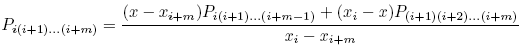
另外,不同級數間的大小差異,也方便地定義了C 與 D 如何從 P 得到:
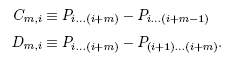
進一步推導,C 與 D 更可以從前一級的 C 與 D 得到
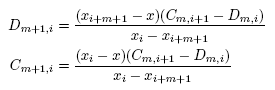
如此,我們再回去看上面那個橫向金字塔,比方說想要得 x 的 P1234,可由 低級數的 P 出發,透過 C 或 D 的求得並附加到 P 上,來獲得較高級數的 P(即在 橫向金字塔 中由左而右)越做越精密, 並且可一路上追蹤不同階數多項式之間的誤差度。
課本提供的副程式是 polint,注意你固然可以有多少個表列點就多少個全用(較危險),你也可以只選其中 m 個(比方說 4 )來用,只選其中 4 個的呼叫副程式方法,以 tabulated values 是 18 組 xx 與 yy 為例,要用到點 15 ~ 18 的作法是:
call polint( xx(15), yy(15), 4, x, y, dy )
而有別於全部 18 組都使用的
call polint( xx, yy, 18, x, y, dy )
提醒大家,在 Fortran 的語法裏, call polint( xx, yy, 18, x, y, dy ) 就是 call polint( xx(1), yy(1), 18, x, y, dy ) 的意思,即呼叫副程式所傳的引數是陣列或變數的起始位置。
我們前面已經建立了從兩個點唯一決定一條直線的線性插值法, 那麼在已知一系列表列點的情況下,被要求要插值某 x 點上求 y,自然我們必需取用 xi < x < xi+1 的那兩個點 ( xi , yi ) 及 ( xi+1 , yi+1 ) 來做線性插值。簡單的說,現在的問題是,給定 x,如何找到 i ?
我們可以想像,若把程式寫成從最小或從最大的表列點開始與 x 比對,萬一 x 值離那端很遠就會沒有效率 。課本提供了二分法 (bisection) 的方法,首先先判斷 x 有沒有小於 x1 或 大於 xN,若確定 x 在其中則拿其中間點 xN/2 (若 N 非偶數就用 N+1)或來與 x 比,判斷出 x 是在 x1 與 xN/2 之間或是 xN/2 與 xN 之間,然後重覆策略,每次都是取用新上下限的中間點去搜尋 。課本提供 locate 副程式給讀者作二分法搜尋,詳見之。 以下圖例:
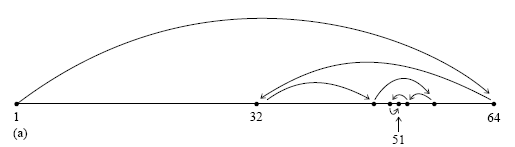
如果我們要做一系列相鄰插值點的插值,比方說要做圖產生圖點用,則每個新點會鄰近於舊點。若每次都由最大範圍的上下限開始用二分法,則會花很多冤枉工。有效的策略應是,每次找表列點時,從上一次獲得的表列點開始,如此有最大的機會命中,若小於 x,則以次兩倍步幅變大跳躍向右尋找,直到找到的點比 x 大,再改用 bisection,這樣較有效率。 課本提供 hunt 副程式做上述工作,詳見之。 以下圖例:

最後,還有一個問題:雖然用 locate 或 hunt 可以由 x 得 j,其中 j 與 j+1 表列點會把 x 包夾住,但像是多項式插值法,若我們一次要用(一共是 N 個點中的)m 個點(m 比方說是 4),能使用 j-1、j、j+1、j+2 當然很好,但若 j 太靠近兩側,例如 j 是 1 或 j+1 是 N 的話,j 就不能選作是那 m 個點的中間點了,這樣要如何處理? 答案:使用下列指令,針對 j、m、N 去作運算,則會把邊邊調到剛剛好,為什麼?可自己想一想。
k = min( max(j-(m-1)/2,1) , N+1-m )
呼叫副程式時,像這樣
call polint( xx(k), yy(k), m, x, y, dy )
以下提供如何使用本節之副程式的範例主程式:
首先第一個例子,這個範例提供 polint 插值的兩種可能用法於同一個主程式中,一個是使用者給一個 x,程式就給一個 y;另一個方法是問範圍及點數,然後程式在此範圍產生等間距的細密插值點(適合作圖用)。
program polint_main
c In subroutine polint, array declaration is used for xa(n) and ya(n),
c for this we need to reclare larger or equal size xa(n) and ya(n) in
c this main program. As for NMAX and c(NAMX) and d(NAMX) in that routine,
c they are taken care locally in that routine alreay with specific size
c (parameter) given when declaring array, therefore we don't need to deal
c with that.
implicit none
integer max_tabu, ngrids_max, n_tabu, m, i, j, k, choice
integer k1, k2, more_points, ngrids
parameter (max_tabu = 100, ngrids_max = 2000)
real xa(max_tabu), ya(max_tabu), x, y, dy, delta_x
real x_plot(ngrids_max), y_plot(ngrids_max),dy_plot(ngrids_max)
real x_min, x_max
character*40 filename1
c Ask filename and the number of tabulated points in the file.
write(*,*) 'Type in the file name of tabulated values (x,y)'
read (*,*) filename1
write(*,*) 'How many points are there in the tabulated set ?'
read (*,*) n_tabu
if (n_tabu.gt.max_tabu) stop 'Too many tabulated values,
& please recompile the main program with a larger max_tabu.'
c Open the file and read in the tabulated values, and write to screen
c for double check.
open (unit = 20, file = filename1)
do i = 1, n_tabu
read (20,*) xa(i), ya(i)
write(*,*) xa(i), ya(i)
end do
close (20)
c Ask the order of polynomial to be usedfor interpolation, not higher
c than 10.
1000 continue
write(*,*) 'How many points do you want to form polynomial ?'
write(*,*) 'For eample, 2 points mean linear interpolation.'
read (*,*) m
if (m.gt.10) then
write(*,*) 'Waring : Neumarial Recipe default max is 10.'
write(*,*) 'Please decress your value or set a bigger NMAX'
write(*,*) 'in the subroutine polint.'
write(*,*) 'Your choice (0 : exit) or (1: input again).'
read (*,*) choice
if (choice.eq.0) stop 'Terminated by user.'
if (choice.eq.1) goto 1000
goto 1000
endif
c One can choose to type in x one by one or to generte a continuous set
c for graph plotting.
write(*,*) 'What do you want to do ?'
write(*,*)'0:input x, find y ; 1:generate a set of points (x,y)'
read (*,*) choice
c This part get x one by one, using "locate" to find the right interval.
if (choice.eq.0) then
1002 write(*,*) 'Type in your x:'
read(*,*) x
call locate (xa, n_tabu, x, j)
k = min( max(j-(m-1)/2,1) , n_tabu+1-m )
call polint(xa(k), ya(k), m, x, y, dy)
write(*,*) 'Interpolated value is ', y, ', error is ', dy
write(*,*) 'One more point (yes=1;no=0) ?'
read (*,*) more_points
if (more_points.eq.1) goto 1002
endif
c This part generate a set of x, using "hunt" to find the right interval.
c The resulting (x,y) is written out into a file named by user.
if (choice.eq.1) then
write(*,*) 'Type your range x_initial and x-final:'
read (*,*) x_min, x_max
write(*,*) 'How many points do you want to plot ?'
read (*,*) ngrids
if(ngrids.le.1) stop 'Need at least two grids.'
delta_x = ( x_max - x_min ) / (ngrids - 1)
j = 1
do i=1, ngrids
x = x_min + (i-1)*delta_x
call hunt(xa, n_tabu, x, j)
k = min( max(j-(m-1)/2,1) , n_tabu+1-m )
x_plot(i) = x
write(*,*) 'x is ',x_plot(i),' j is ',j,' k is',k
call polint(xa(k),ya(k),m,x_plot(i),y_plot(i),dy_plot(i))
end do
write(*,*) 'Plrease give a name to your output file:'
read (*,*) filename1
open (unit=30, file=filename1)
do i=1,ngrids
write(30,*) x_plot(i), y_plot(i)
end do
close(30)
write(*,*) 'Info: Error estimate will be written into file
&error.dat'
open (unit=40, file='error.dat')
do i=1,ngrids
write(40,*) x_plot(i), dy_plot(i)
end do
close(40)
end if
end
另外,當你要利用插值法來配合繪圖,以下是一個範例程式:
program polint_pgplot
integer ntab_max, nplot_max
parameter (ntab_max = 20, nplot_max = 200)
real x_tab(ntab_max), y_tab(ntab_max), x_min, x_max, delta_x
real x_plot(nplot_max), y_plot(nplot_max), dy_plot(nplot_max)
integer ntab, i, nplot, m, j, pgopen
character*40 filename1
write(*,*)'Please tell me the number of tabulated values:'
read(*,*) ntab
write(*,*) 'Which filename contains the tabulated value ?'
read(*,*) filename1
open(unit=10, file=filename1)
do i=1,ntab
read(10,*) x_tab(i), y_tab(i)
end do
close(10)
write(*,*) 'Type in min and max of x:'
read(*,*) x_min, x_max
write(*,*) 'How many points to draw ?'
read(*,*) nplot
write(*,*) 'How many point to form polynomial ?'
read(*,*) m
delta_x = (x_max - x_min) / (nplot - 1)
do i=1, nplot
x_plot(i) = x_min + (i-1) * delta_x
call hunt(x_tab,ntab,x_plot(i),j)
k = min( max(j-(m-1)/2,1) , ntab+1-m )
call polint(x_tab(k), y_tab(k), m, x_plot(i), y_plot(i),
& dy_plot(i))
end do
do i=1,nplot,10
write(*,*) 'x_plot and y_plot,', x_plot(i), y_plot(i)
end do
if ( pgopen('?') .le. 0 ) stop
call pgenv(2.0, 6.0, 0.0, 40.0, 0, 1)
call pgline(nplot, x_plot, y_plot)
call pgpt(ntab, x_tab, y_tab, 9)
call pgclos
end