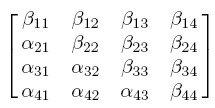要證明其存在,我就根據所給的資料把該物件做出來,由於這是一般性而無特殊性的,因此證明了該物件的存在或該特性的成立。
在本單元中,我們要證明任何任方陣 A 都可以被分解寫成 A = L U 兩個方矩陣的形式,在作法上,我們就先大膽地寫下如課本 (2.3.2) 式的式子:

在不失一般性的情況下,我們可以令 所有對角線上的 aii 都等於 1。這樣做真的沒問題嗎?真的可只有一組 L 與 U 可以得得到嗎?我們先不要怕麻煩,試著一個一個來看 aij 與 bjk 乘在一起如何形成 aik 。最簡單的是第一個,已經說好了 aii 都等於 1,因此 b11 = a11。再往下看一個,是 a21b11 = a21,而 b11 剛才己經得知是 a11,因此 a21 就自動知道了。同理, a31 與 a41 也都是類似的方法輕易得知。再來,我們看 U 方陣第二列乘向 L 方陣那四列的結果,(記得 a 的 11、21、31、41 都己經知道了)乘 L 的第一列會逼出 b12 的值。 乘到 L 的第二列時,由於 a22 為 1,就確定了 b22 。在 b12、b22 都是己知的情況下,乘第三列會定出 a32,同理乘第四列會定出 a42 ,如此 L 方陣的第二行也定完了。再接下來是拿 U 虧陣的第三行乘到 L 方陣的四個行,依序定出 b13、b23、b33、a43。最後,相同的策略會依序給出 b14、b24、b34、b44,如此所有 L 及 U 方陣的元素就都唯一確定了。我們因此建構式地證明了(在 4x4 的例子中)L U = A 的可行性。
總言之,若以 L 與 U 寫在一起的緊密形式來看
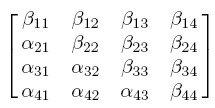
上式元素依序定出的順序如下:
| 1 |
5 |
9 |
13 |
| 2 |
6 |
10 |
14 |
| 3 |
7 |
11 |
15 |
| 4 |
8 |
12 |
16 |
本節所用到的副程式有兩個,分別是作 LU 分解的 ludcmp,以及做配合其作反向代回的 lubksb 。 這兩個副程式的呼叫引數 (argument) 安排與課文內說明分別如下:
SUBROUTINE ludcmp(a,n,np,indx,d)
INTEGER n,np,indx(n),NMAX
REAL d,a(np,np),TINY
PARAMETER (NMAX=500,TINY=1.0e-20) Largest expected n, and a small number.
Given a matrix a(1:n,1:n), with physical dimension np by np, this routine replaces it by
the LU decomposition of a rowwise permutation of itself. a and n are input. a is output,
arranged as in equation (2.3.14) above; indx(1:n) is an output vector that records the
row permutation effected by the partial pivoting; d is output as ±1 depending on whether
the number of row interchanges was even or odd, respectively. This routine is used in
combination with lubksb to solve linear equations or invert a matrix.
INTEGER i,imax,j,k
ludcmp 需要從主程式配合宣告的是 a(np,np),以及傳入整數值 n,就這樣而已,剩下的引數 indx 及 d 則是為了之後銜接 lubksb 解線性代數問題之用(ludcmp 只作矩陣 A 的今分解)。
SUBROUTINE lubksb(a,n,np,indx,b)
INTEGER n,np,indx(n)
REAL a(np,np),b(n)
Solves the set of n linear equations A · X = B. Here a is input, not as the matrix A but
rather as its LU decomposition, determined by the routine ludcmp. indx is input as the
permutation vector returned by ludcmp. b(1:n) is input as the right-hand side vector B,
and returns with the solution vector X. a, n, np, and indx are not modified by this outine
and can be left in place for successive calls with different right-hand sides b. This routine
takes into account the possibility that b will begin with many zero elements, so it is efficient
for use in matrix inversion.
INTEGER i,ii,j,ll
REAL sum
lubksb 一次只作一個直行的 b 向量,不像是 Gauss-Jordan 那樣做 column-augmented 之多重 b 的組合。 這是沒有必要的,因為原題目給的矩陣 A 業經分解為 L 與 U,求解快又有效率。 呼叫過 lubksb 之後,答案 x 會存在 b 的位置傳出來。
如果要求解 A 的反矩陣 A-1,我們可以在主程式中安排多個 b 向量,每一個依序都是構成單位矩陣的一直行,如此多次呼叫 lubksb 解出各對應的行向量 x 來加以組合,就會得到反矩陣 A-1。詳細作法(程式碼)課文中有。
若要求行列式值,則在主程式中寫個簡單的迴圈,把分解後傳出之矩陣 a 其上之對角線上的元素(即 bii 連乘起來,就是 det(U),這是因為三角矩陣的行列式特別容易,就是對角元素的連乘積,這裏有用到 det(A) = det(LU) = det(L)det(U) = 1.det(U) = det(U)。)。 詳細作法的程式碼亦可見課文。這裏的重點是,U 矩陣的對角元素積,還要再乘上利用 ludcmp 回傳的 d 值,才是最後正確的行列式值(由於 pivoting 之行列交換所造成的正負差異是存在 d 裏面)。
program lu_main
implicit none
integer n, np, i, j
parameter (np=10)
integer indx(np)
real a(np,np), b(np), d
character*40 filename1, filename2
write (*,*)'Please tell me the dimension n of the matrix A(n,n):'
read (*,*) n
write (*,*) 'Please give the file name that contains A :'
read (*,*) filename1
write (*,*) 'Please give the file name that contains b :'
read (*,*) filename2
open (unit=20, file=filename1)
do i=1,n
read (20,*) ( a(i,j), j=1,n )
enddo
close(20)
open (unit=20, file=filename2)
do i=1,n
read (20,*) b(i)
enddo
close(20)
call ludcmp(a,n,np,indx,d)
call lubksb(a,n,np,indx,b)
write (*,*) 'The solution matrix is :'
do i=1,n
write (*,*) b(i)
enddo
do i=1,n
d = d * a(i,i)
end do
write(*,*) 'The determinant is', d
end