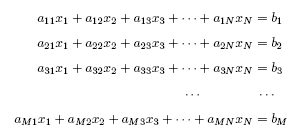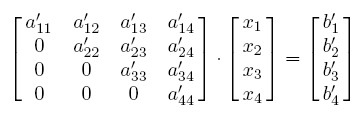線性代數問題：數學問題剖析、高斯－佐丹消去法

課程要點提示

 

破題：線性代數方程式的解

方程式與函數有什麼不同？

什麼是求解？（把未知數變成已知的過程）

什麼是解？（能符合原方程式之未知數的數值、函數，或關係式）

什麼是代數方程式？（有別於微分方程式）

方程這個辭是怎麼來的？

什麼是線性？

什麼是線性代數？

什麼是線性組合？

一個線性方程組的其中一條方程式，在幾何上具有什麼樣的意義或圖像？（高維度空間的直線方程式）

 

線性代數方程式（組）的一般形式是什麼？

線性代數方程式

其中所有 aij 及 bi 都是己知，所有 xj 都是未知，若不是如此，就不是線性代數方程式了。

若未知數的個數與方程式的個數相同，即 N = M，則上式方程組有可能可以有唯一解。解析上而言，如果某一條方程式是其他方程式的線性組合，就形成了行簡併。（什麼是簡併）或所有方程式共同含有某幾個變數的特定組合方式，如 x5 所有系數與 x3 與 x4 系數所有呈線性組合關係，則成列簡併。（在 N = M 的情況下，有行簡併就一定有列簡併，並且我們稱此方程式為奇異的（singular）。

 

線性代數方程式（組）其解的不變性

線性代數方程式的解有一些有趣的不變性，也說是說，原方程組作某些外觀或形式上的改變，對其解並無影響。

以二元一次方程組

ax + by = c

dx + ey = f

為例，想想看怎樣的題目變化仍會讓其 x、y 的解保持不變？

行對調

dx + ey = f

ax + by = c

加法本來就可以交換

by + ax = c

ey + dx = f

列交換（x 與 y 的角色會對調）

bx' + ay' = c

ex' + dy' = f

任一式整個（等號兩邊）同乘某係數

k(ax) + k(by) = k(c)

dx + ey = f

等號兩邊加減同量

(a-d)x + (b-e)y = c-f

dx + ey = f

 

 

Gauss-Jordan 消去法

大家在中學時有學過 高斯消去法求反矩陣，你們用的物數教科書剛好也有，我掃描下來給大家複習之用 Arfken page。

Gauss-Jordan Inversion 1
Gauss-Jordan Inversion 2

為什麼這樣做就下去，右邊的就是反矩陣？

假設我們不知道反矩陣 A-1 是怎樣，寫作 Y（用 Y 是取其常作為變數之用的意思），就有 A Y = I，如此，在 Y 的解不變的情形之下，一路整理到 A' Y  = I' -> A'' Y = I'' -> ... -> 直到 I Y = [某矩陣]，而 Y 解的本質依某原本的定義是 A-1，因此該 [某矩陣] 就是 A 的反矩陣了。

求 A 的反矩陣有什麼用？不是要解 A x = b 嗎？

有了 A 的反矩陣，我們知道 A-1 A x = A-1 b，因此就直接有 x = A-1 b 而把解算出來。

 

在Numerical Recipe 課文中，作者特別出三種改造簡化原方程式（而其解仍不變）的動作，其中第二點就是操作高斯佐丹消去法的基本依據，請大家注意一下。

 

Column-Augmented 表示法

考慮以下兩個線性代數方程組 Ax = b、 Ay = c 依照矩陣作用在列向量的運算規則，它完全可以合併成為 A[x y] = [b c] 而完全不影響 [x] 及 [y] 列向量的解。

到此我們可以理解，只要能把上述動作寫成程式，配合 Column-Augmented 資料排列方式，我們就可以有一個求解 Ax = b 之 x 以及 AY = I 之 Y 的自動化方法了。

 

Pivoting

為了讓數值運算的過程達到最高的精確度及穩定性，我們儘可能要把最大的元素調到對角線上的位置，若是作列對調，則解不受影響；若作行對調，則解仍不變，只差涉及刻對調列那兩個對應的待求解未知變數的角色要對調（例如，第三列與第五列對調，則 x3 與 x5 的角色要互換）。在有包含列對調功能的 Gauss-Jordan 程式中，程式會追蹤記錄所發生過的角色互換而在最後印出答案前把它們調換回來，課本中的程式就是這樣。

 

副程式之使用

由於這是大家第一次學習使用 Numerical Recipe 上的程式，我把使用的步驟與要點講仔細一點。

首先，看清楚課文中副程式裏的說明文字敘述（電子檔沒有，課文才有），像是藍色的這一塊：

SUBROUTINE gaussj(a,n,np,b,m,mp)
INTEGER m,mp,n,np,NMAX
REAL a(np,np),b(np,mp)
PARAMETER (NMAX=50)
Linear equation solution by Gauss-Jordan elimination, equation (2.1.1) above. a(1:n,1:n) is an input matrix stored in an array of physical dimensions np by np. b(1:n,1:m) is an input matrix containing the m right-hand side vectors, stored in an array of physical dimensions np by mp. On output, a(1:n,1:n) is replaced by its matrix inverse, and b(1:n,1:m) is replaced by the corresponding set of solution vectors.Parameter: NMAX is the largest anticipated value of n.
INTEGER i,icol,irow,j,k,l,ll,indxc(NMAX),indxr(NMAX),

這裏面描述了作為輸入時，a、b 陣列各是什麼以及它們的大小 n、m、np、mp 等。 也提到了作為輸出時，陣列 a、b 又各自具有什麼意義。

其次，我們自己要寫一個主程式來叫用 gaussj 副程式。注意 gaussj 中有宣告 a(np,np)、b(np,mp) 會用到整數值 np 及 mp ，我們當然不會希望每次要用 gaussj 就去改到它的內容，這就必須由在主程式就作好宣告，讓副程式來繼承。則我們在主程式中的作法如下（以 a 是 3x3、b 是 column vector 3x1 為例）：

program gauss_main
real a(3,3), b(3,1)
integer n, np, m, mp, i
parameter (np=3, mp=1)

或是，稍微再高竿一點

program gauss_main
integer n, np, m, mp, i
parameter (np=3, mp=1)
real a(np,np), b(np,mp)

np、mp 必須先宣告成整數，這是本來就要做的。一旦使用了 parameter 指令把這些整數變數的數加以指定（在整個程式中它們的值都不會再改變，可視為是一個常數而不再是變數），我們就可以用來宣告陣列，這是因為編譯器已明確地知道 np、mp 的值是多少了。這樣，不但主程式中的宣告完成，也可以讓副程式 gaussj 的宣告妥當，我們在此檢視一 副程式 gaussj 在宣告 a、b 的部分：

SUBROUTINE gaussj(a,n,np,b,m,mp)
INTEGER m,mp,n,np,NMAX
REAL a(np,np),b(np,mp)
PARAMETER (NMAX=50)
INTEGER i,icol,irow,j,k,l,ll,indxc(NMAX),indxr(NMAX),ipiv(NMAX)
REAL big,dum,pivinv

你看，它是直接宣告 REAL a(np,np),b(np,mp)，這樣就可以了，我們完全不必更改 gaussj 的內容。

一個簡易的，能呼叫副程式 gaussj 的主程式（假設 a 是 3x3、b 是 3x1）如下：

program gauss_main

integer n, np, m, mp, i
parameter (np=3, mp=1)
real a(np,np), b(np,mp)

n=3
m=1

open (unit=20, file='a.dat')
do i=1,3
read (20,*) a(i,1), a(i,2), a(i,3)
enddo
close(20)

open (unit=20, file='b.dat')
do i=1,3
read (20,*) b(i,1)
enddo
close(20)

call gaussj(a,n,np,b,m,mp)

write(*,*) 'The inverse matrix is :'
do i=1,3
write (*,*) a(i,1), a(i,2), a(i,3)
enddo

write (*,*)

write (*,*) 'and the solution matrix is :'
do i=1,3
write (*,*) b(i,1)
enddo

end

一個功能較完整，能處理不同矩陣大小問題的主程式範例如下，重點我以彩色標出：

program gauss_main2

integer n, np, m, mp, i
parameter (np=10, mp=20)
real a(np,np), b(np,mp)
character*40 filename1, filename2

write (*,*)'Please tell me the dimension n of the matrix (n,n):'
read (*,*) n
if(n.gt.np) stop 'n can not be larger than np'

write (*,*) 'Please give the size m of the augmented b(n,m):'
read (*,*) m
if(m.gt.mp) stop 'm can not be larger than mp'

write (*,*) 'Please give the file name that contains A :'
read (*,*) filename1
write (*,*) 'Please give the file name that contains b :'
read (*,*) filename2

open (unit=20, file=filename1)
do i=1,n
read (20,*) ( a(i,j), j=1,n )
enddo
close(20)

open (unit=20, file=filename2)
do i=1,n
read (20,*) ( b(i,j), j=1,m )
enddo
close(20)

call gaussj(a,n,np,b,m,mp)

write(*,*) 'The inverse matrix is :'
do i=1,n
write (*,*) ( a(i,j), j=1,n )
enddo
write (*,*)
write (*,*) 'and the solution matrix is :'
do i=1,n
write (*,*) ( b(i,j), j=1,m )
enddo

end

 

 

最後，我們要把 主、副程式編譯並鏈結在一起造出可執行檔，這要進行以下的動作：

gfortran -o my_gaussj.x gauss_main.f gaussj.f

或者是先用 -c（compile only）得個自 .o 檔後再 link 在一起如下：

gfortran -c gauss_main.f
gfortran -c gaussj.f
gfortran -o my_gaussj.x gauss_main.o gaussj.o

這其中會遇到警告訊息，但這是無害的

測試也是很重要的。程式剛寫好時，你可以用一個己經或很容易知道答案的題目先作測試，例如 a、b 分別為：

1 0 0
0 2 0
0 0 4

及

1
1
1

有了上述數據作為檔案 a.dat 與 b.dat 的內容，放在與可執行檔 my_gauss.x 同一個目錄下，打 ./my_gauss.x，答案就會列出到螢幕上了。

 

補充資訊

Cramer's rule ：用於求解 Ax = b 之解析公式，用到求行列式值。維基百科中的介紹

以下更多來自維基百科的介紹

Systems of linear equations belong to the oldest problems in mathematics and they have many applications, such as in digital signal processing, estimation, forecasting and generally in linear programming and in the approximation of non-linear problems in numerical analysis.

Linear algebra is the branch of mathematics concerned with the study of vectors, vector spaces (also called linear spaces), linear transformations, and systems of linear equations. Vector spaces are a central theme in modern mathematics; thus, linear algebra is widely used in both abstract algebra and functional analysis. Linear algebra also has a concrete representation in analytic geometry and it is generalized in operator theory. It has extensive applications in the natural sciences and the social sciences, since nonlinear models can often be approximated by a linear model.

 

線性代數問題：反向代回法（Back Substitution）

 

反向代回法（Back Substitution）

讓我們現在來考慮一個與前一節不太一樣的情況，假設我們使用 Gauss-Jordan 方法，並不把原來的線性代數方程式的 A 矩陣代簡到成為單位矩陣，而是只化到成為三角矩陣，像下面的例子那樣：

back-subs

注意新的 A' 矩陣是一個上三角矩陣，其元素已經打上了 prime 標號以代表與原有的 aij 不同，另外傍隨要變的常數向量 b' 也作 prime 標記，而要求解的 xi 則仍是原來的 xi 沒有變。這是使用高斯消去法我們會預期的特性。

把一個線性代數方程式整理到像上式的模樣，我們雖然失去了直接獲得反矩陣的機會[註]，但卻能很快地得出對應於向量 b' 的解向量 x。直接觀察最下面的一列方程式，我們馬上可以從上式得到 x4 的答案，然後在知道 x4 的情況下， 往上看我們又立即確定了 x3 的值，再往上就又唯一決定了 x2，如此到了最上面一列 x1 也定出來，在這個逐一求解的過程中，前一步求出之未知數在求下一個都剛好有用上，這叫反向代回法 (back-substitution)（若今天是呈下三角矩陣的形式，則是正向代入法 (forward-substitution) ），大家很清楚地可以看出這是一個簡明而快速的方法。

[註]：即便不能直接自動獲得反矩陣，在 column-augmented 形式下，我們仍可以用 幾個 b 向量來 "組合" 成一個單位矩陣，如如此解得的 column-augmented 之 x 向量組就恰好會是 A 的反矩陣了。

Backsubstotution 這個方法的應用價值會在下一個單元 LU Decompotion 方法中，更加突顯出來。