IV

Local and Partly Local Pseudopotentials

from

A Non-local Method

( How Local Can One Make A Pseudopotential )

The purpose of this chapter is to demonstrate further how to apply the Projector Reduction method, introduced in Chapter III, in generating pseudopotentials of elements in various categories. This also allows us to carry out a systematic investigation of the non-locality of pseudopotentials of the corresponding chemical elements, which helps us to understand why some elements can be reasonably represented by a local pseudopotential while for some others a non-local one is necessary. In the other words, we want to ask whether good local pseudopotentials for some particular elements probably exist but are yet to be found, or whether it is fundamentally impossible to treat them reliably by using local pseudopotentials.

IV.1. Introduction

In Chapter III we showed how the systematic procedures of Chapter II can be used to generate pseudopotentials that are partially local i.e. have nearly the same V_l(r) for two or more different l, so that when a weighted average of them is chosen as V^L(r), those corresponding dV_l (r) will be sufficiently small to be ignored, which makes the l dependence of those V_l(r) disappear.

In this chapter we apply this to different types of atom in different parts of the periodic table, to see how far one can push this in practice. The extreme situation is that, to a sufficient degree of approximation, one can use the same V_l(r) for all l, i.e. one can use a local pseudopotential. There are a few elements, particularly Al, Ge and As, for which local potentials have been used for several years with reasonable success. This raises the question whether there is something special about these elements, or whether there is a realistic possibility of generating equally good local pseudopotentials for more atoms. Computationally that would clearly be very desirable.

All the examples and tests discussed in this chapter are restricted to non-f elements i.e. those not having any valence electron in the 4f or 5f shells in the atomic state, although there is no obvious reason why the basic idea presented in this chapter can not be applied to the elements with occupied f or even higher l-states. Since the central issue of the non-locality of a pseudopotential is the l-dependency of each V_l (r), it will be useful to know which and how many V_l(r) should be considered in general. A non-local pseudopotential in practice contains only V_l (r) for a few lower l, which may seem inappropriate for Bloch functions which in general contain components of all angular momenta. However, with a simple argument we can demonstrate the trend that higher the l is, less important the V_l (r) will be, which justifies the use of only V_l (r) with lower l in a non-local pseudopotential because they are the dominant components. Our estimate also suggests that l=0,1,2 should be enough for non-f elements.

We make the argument by first assuming the delocalised (valence) electrons in a given system to be free-electron-like. The maximum linear momentum (i.e., the Fermi momentum) of the system can then be expressed in terms of the density of electron gas. One can then estimate the typical value of angular momentum of the system in terms of the incoming momentum and the impact parameter, as in the case of a classical scattering problem. The magnitude of the angular momentum estimated this way depends purely on the density, which will give us some idea about the maximum angular momentum of the given electron gas system in terms of the number of delocalised electron per atom ratio. More precisely, from the free electron approximation, the Fermi momentum k_F of free electron gas is determined by the charge density r, in atomic units (m_e = h/2p = e = 1),

. (1.1)

Let r₀ be the Wigner-Seitz radius of the atom. The classical scattering picture suggests that the largest angular momentum l_max that can exist in the system is the largest possible linear momentum k_F multiplied by the largest possible impact parameter r₀ :

. (1.2)

The mean charge density r in (1.1) can be written in terms of the total number of electrons N in the Wigner-Seitz cell,

. (1.3)

If we introduce (1.3) and (1.1) into the (1.2), then the l_max becomes

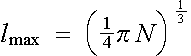. (1.4)

Estimated this way, the l_max is only a function of N, i.e. the number of valence (conduction) electrons per atom. We can now use (1.4) to find out the value of l_max that corresponds to a given N. For the state l = 3 to start to be important, the value of N has to reach about 10 (so that l_max > 2), while for l = 1 to be effective, the N only needs to be larger than 1. It is obvious that in most cases in real applications, N takes the value between these two numbers, which means that l = 2 should be sufficient for a free-electron-like system.

When there are more localised electronic states exist in the system, such as in the case of a molecule or when there are d or f electrons in a solid, the situation will be different. However, in these systems these localised states should at least be less localised than those in an atom. Thus as long as a pseudopotential carries a component matching the highest l of the occupied atomic ground state, it should be sufficient to describe the scattering in a solid.

From the above reasoning we believe that, for both a delocalised (free-electron-like) system and highly localised system such as a transition metal, our simple picture explains why, for a non-f element, a non-local potential with s, p, and d components together should be enough for a faithful representation of the major l dependent non-local effect. In addition, we believe that a straight-forward extension of this argument can be made to cover the f-elemeents, in which case we think a non-local pseudopotential carrying V_l(r) of s, p, d and f should be sufficient.

It worth emphasising that the above argument also justifies the conventional way of writing V_l(r) as

V_l(r) = V ^L(r) + dV_l(r) , (1.5)

in which (for non-f elements) those dV_l(r) for l > 2 are set to zero to save computing, leaving only the V^L(r) to operate on components of wave functions for all l > 2 . It is widely known that the V^L(r) can be fairly arbitrary chosen (to avoid ghost state in KB form) without affecting the results of calculation [Ref.K.2, G.1], which is consistent with our argument that the electron-ion interaction with l > 2 is not important anyway and therefore the results of calculation are insensitive to the actual value of V_l(r) used (in this case, V ^L(r)). As for l = 2, we will see from the study of Al in Section 3 that there are cases when V_d(r) is important.

In Section 2 we discuss making V_l(r) effectively the same for s and p components in some elements, and for p and d in other elements. In Section 3 we consider Al, Si and Ge in detail in relation to finding fully local (approximate) pseudopotentials for these elements. A short discussion and conclusion is given in Section 4.

IV.2. Reducing The Non-locality in Different Cases

The feasibility of reducing the number of projectors in a pseudopotential depends mainly on the nature of the atomic orbitals of a given element. We find it convenient to discuss the procedure in two categories, namely those involving pd reduction and those involving sp reduction, with each category further classified by whether there exists a cancellation effect [Ref.H.2] in the pseudopotential. Atomic logarithmic derivative tests are always used to examine the success of the reduction. Detailed generating and tuning parameters as well as figures of V_l(r) and logarithmic derivatives are given for each pseudopotential mentioned.

pd reduction

For elements such as C, N, O, both of their 2p and 3d radial wavefunctions have no node and there is no cancellation effect from an inner shell to contribute to pseudising the wavefunctions. We have found that for such elements it is relatively easy to redistribute (i.e. optimise) the pseudo wavefunctions for both the 2p and 3d states within the pseudo core without too much restriction, which makes a fairly flexible change of shape of V_p(r) and V_d(r) possible. An extremely high degree of similarity between V_p(r) and V_d(r) of the pseudopotential can therefore be achieved. Two typical examples of such pd "localisation" of the 2p and 3d components can be seen in the case of C and B, as shown in Fig.IV.2.1 and Fig.IV.2.2 respectively. (The detailed generating parameters of this C and B pseudopotentials can be found in Chapter V, which are numbered as C021 and B001a.)

When one or both of p and d wavefunctions have nodes, the possibility of finding a common pseudopotential for both angular momentum channels is more case dependent. Redistributing charge density using Q_c-tuning is usually not as easy as in the cases in which both p and d wavefunctions are nodeless. (The worst case is presumably when l=1 has cancellation but l=2 does not, e.g. 3d transition metals. But in fact even for 4d and 5d transition metals, the V_p(r) and V_d(r) are still quite different, which we believe due mainly to the fact that the location of main charge density peak is very different for their p and d components.) Under this situation, the best we can do is to try to apply the Projector Reduction even though V_p(r) and V_d(r) are not extremely similar. This works alright in some cases, especially those cases in which the d-state is unoccupied in the atomic ground state and should therefore be comparatively less important in solid than the occupied states. An example of the successful localisation pd non-locality within this category is the Br pseudopotential, shown in Fig.IV.2.3. The generating parameter of this Br pseudopotential can be find in detail in the section III.2 of Chapter III.

sp reduction

Unlike in the case of pd localisation discussed above, we are less interested in the case which both s and p that have no cancellation effect because only H and He satisfy such a condition. As for the cases which the valence states are 2s (cancelled) and 2p (un-cancelled), such as C and O, their V_s(r) and V_p(r) components are very different even after applying Q_c-tuning. We therefore think that is essential to keep the individual V_s(r) and V_p(r) in the pseudopotential for those elements. In the cases in which both s and p wavefunctions have nodes, however, we found that it is possible to make V_s(r) and V_p(r) similar. Among the cases explored, we have successfully reduced the sp non-locality for the 3d transition metals that has more than four d electrons, such as Fe, which is shown in Fig.IV.2.4. The full details of the parameter of projector reduced Fe pseudopotential is described in Chapter V as Fe002. From the Fig.IV.2.4(a) we can see that its V_s(r) and V_p(r) are very similar. The logarithmic derivative of the resulting sp reduced Fe pseudopotential is shown in Fig.IV.2.4(b). The similar quality of Projector Reduction has also been demonstrated in the cases of Co and Cu discussed in Chapter III. Experence has shown that the degree of agreement is very satisfactory, giving errors smaller than a typical LDA pseudopotential calculation. Unlike in the case of Fe, our best possible sp localisation for Ge is only marginally acceptable, as shown by the logarithmic derivative tests in Fig.IV.2.5(a) and (b). The Ge pseudopotential was generated using atomic ground state configuration to calculate the s and p wave functions, and the ionic state 4s^1.00 4p ^0.75 4d ^0.25 to calculate the d wave function. The r_c took a typical value of 2.2 a.u. for Ge. To minimise dV_s(r) and dV_p(r) the Q_c/q₃(s, p, d) was set to be (0.7, 0.9, 0.95). The weight 0.8 for the V_s(r) and 0.2 for the V_p(r) were used to construct the V^L(r). A noticeable improvement of logarithmic derivatives can be seen with the dV_s(r) and dV_p(r) of the pseudopotential kept, as shown in Fig.IV.2.5(c), which indicates that the non-locality of s and p may still be needed for a very accurate calculation.

Although Ge is in the same long row of the periodic table as Fe, Co, Ni, Cu, Zn , we observed a clear difference in the degree of similarity that one can achieve between V_s(r) and V_p(r), which in the case of Ge is more difficult than with the mentioned transition metals. The reason may be that for these metals the 4p is an excited state, while for Ge it is occupied (in the atomic ground state). Thus we expect the 4p state of Ge to be more tightly bound and have its main charge density peak at quite a different location from that of the unoccupied 4p state of the transition metals.

IV.3. Case Studies of Al, Si and Ge

Apart from the advantage of saving computing time and memory, the Projector Reduction provides an unambiguous procedure and test for discussing the degree of locality/non-locality of the pseudopotential of a given element, which may help to clarifies some long-term puzzles.

As mentioned in Section 1, reasonably good local pseduopotentials has been in use for Al [Ref.R.2] and Ge [Ref.N.2] but apperently none for Si. In view of the importance of calculations on Si, one may presume that efforts have been made to find a similar local pseduopotential for Si but failed, and there is some folkelore to this effect [Ref.H.3]. Thus case studies of Si/Ge and Al/Si are devised with an attempt to clarify this issue by using our new technique, which generates local or partly local pseudopotentials from a non-local approach. More precisely, since in our method each local or partly local pseudopotential has a coreesponding fully non-local counterpart (i.e. the one with all dV_s(r) kept), the degree of the success in reducing the non-locality of Si, Al and Ge pseudopotemtials can be used as a measure of whether a lequally good local Si pseduopotential is really more difficult to be found (with a reasonable r_c, of course) than a Ge or an Al one.

For the cases stuided in this section, local pseudopotentials of Al, Si and Ge genertaed using Projector Reduction method was prepared. Atomic ground state was used for both Al and Si to calculate their s and p wave functions. The r_c were chosen as the most typical and adequate values for corresponding elements based on our experience, with Q_c tuned to make V_s(r) and V_p(r) similar. (We don't need to deal with V_d(r) for Al and Si here because the V_d(r) is much less imporant than V_s(r) and V_p(r) due to its larger l and the fact that the d state is not occupied in the atomic ground state of these elements.) The resulting r_c and Q_c for Al : r_c = 2.4 a.u., Q_c/q₃(s,p) = (1.10, 1.00), and for Si : r_c = 2.0 a.u., Q_c/q₃(s,p) = (0.6, 0.9). The weight of mixing to construct V^L(r) are 0.8V_s(r) and 0.2V_p(r) for both cases. As for the local Ge pseudopotential, the exactly same one as described in Section 2 is used.

Al and Si Pseudopotentials

As already mentioned, it appears that a local pseudopotential works better for Al than for Si. However, the valence orbitals occupied in the atomic ground states of Al and Si are both 3s and 3p, so that one does not expect any difference to come from the inner level cancellation. In fact, by analysing the logarithmic derivative of both "localised" pseudopotentials of Al and Si described above (shown in Fig.3.1 and Fig.3.2 respectively), we have found that the degree of non-locality in them is indeed fairly similar. This implies that the defferent performance of local pseudopotentials for these two elements, if it exists, is not due to their atomic nature such as cancellation from core states or the profile of the wavefunctions, but nust come mostly from their different situation in the solid state. An obvious difference between Al and Si in their solid form is that Al is a close-packed metal and Si a semiconductor with a more open structure (mole volume of Al : 10 cm³/mole, Si : 12 cm³/mole). Since there are only 4 nearest neighbours for each Si atom in its diamond structure, in contrast to 12 for Al as an fcc metal, the chemical bonds between Si atoms are more directional than those between Al atoms. It may, therefore, be the covalency of the system which leads to the need for a more accurate non-local description from a Si pseudopotential. For example the directional bonds depend on sp hybridisation and thus may be sensitive to the difference between the s and p pseudopotentials. In brief, we find that Al and Si have the same degree of non-locality, which suggests that the greater acceptability of an Al local potential is probably due to the higher tolerance of the system.

Si and Ge Pseudopotentials

Although we have pointed out in the begining of this section that the V_d(r) is less important than V_s(r) and V_p(r) for elements such as Al, Si and Ge. It can be understood from our free-electron analysis (1.4) that, since both Si and Ge have the number of valence electron N = 4 which results in the effective l_max for Si and Ge being 1.46 and larger than 1 (i.e. the l for p-wave), the electronic states with d symmerty may not be completely ignored in the solid Si and Ge. Since a local potential acts on all l state, it will be useful to see whether our local potentials of Ge and Si produce equally good or bad d-scattering, which might still have a modist importance for a solid.

We have tested the d logarithmic derivatives (all-electron and pseudo) of the projector reduced local pseudopotentials for Si and Ge, as shown in Fig.IV.3.2(c) and Fig.3.3(b) respectively. Although the logarithmic derivatives of the pseudo wave functions for both Ge and Si cases do not match the nearly perfect agreement with all-electron values as we had found with C and B with 2p-3d reduction (described in Section 2), they do clearly show that the local pseudopotential of Ge is not as bad as that of Si in reproducing the d-scattering. This can be understood from the fact that the cancellation effect from inner shells exists for the 4d orbital of Ge but not for the 3d orbital of Si, which results in the V_p(r) and V_d(r) from the 4p and 4d states of Ge being more or less similar, whereas those from the 3p and 3d states of Si are very different. Therefore from the view point of the d-component, the Ge pseudopotential is more "local" than a Si one due to it atomic nature. As for s and p, we have shown in Section 2 and Fig.IV.2.5(b) that the quality of the sp partly-local Ge pseudopotential is only marginally acceptable, but it is still better, or at least not worse, than the similar case of Si, as shown in Fig.IV.3.2(b). From the overall comparison of Ge and Si we find that there is a noticeable difference in locality, which supports the common experience that one can use a local potential for Ge but not for Si.

The atomic nature of Ge not only allows its pseudopotential to be more local than that of Si, but it also helps to reduce the pseudopotential error. This is because Ge has a larger principle quantum number n for its valence s-state than Si has (n = 4 for Ge, n = 3 for Si). Due to this bigger n as well as the larger core size, the overlapping of the s orbitals of neighbouring atoms of Ge is less than in the case of Si, which leads to a narrower s (sp) band. All those 4s-derived Bloch states of Ge are therefore not as far away from its atomic 4s level compared with the 3s-derived Bloch state of Si from its Si 3s level. Based on the fact that a pseudopotential only reproduces scattering within a finite range of energies, we can say that the smaller s overlap in Ge makes the results of solid state calculation less sensitive to the error from a (local) pseudopotential of Ge compared with Si. (Actually, this is the solid state analogue of an important chemical effect called the "inert s-pair effect". It explains why there is a tendency for the s electrons of the heavier elements to have lower chemical reactivity than those from the lighter ones in the same column of the periodic table which have analogous valence electronic configuration.)

In conclusion, we have shown that the pseudopotential of Si is inherently somewhat more non-local, in agreement with general experience, for reasons which we have traced to differences in the atoms.

A critical re-appraisal of Al : a p-local s-non-local Al Pseudopotential

Like in the case of Ge and Si discussed above, the free-electron estimatation also suggests that the V_d(r) can still play some role in a solid Al becasue it has 3 valence electrons, giveing an effective l_max as 1.33, which is already larger than 1. In fact, there is a pure d symmetry at the corner of the Brillouin zone less than 1 eV above the Fermi level so that significant l = 2 components whould be expected also below E_F. However, a local pseudopotential for Al works fine in reproducing some basic of solid-state bulk properties. This is probably because an accurate angular dependency of the electronic structure is not so important in those calculations. The point is that angular effects depend critically on the degree of hybridisation between s, p and d orbitals in a chemical tight binding picture. In metals this translates into the right type and degree of mixing among the l = 0, 1 an 2 components of Bloch functions. which depends sensitively on the differences between the V_l (r) with l = 0, 1, 2. The latter are swept aside in the approximation of a local pseudopotential, which can therefore be expected to fail in describing subtle structural properties, such as surface energy [Ref.G.1] and the energy stacking fault and defect [Ref. P.1]. We must therefore have a pseudopotential which takes V_d(r) properly into account as well as V_s(r) and V_p(r).

On the other hand, due to the efficiency of using a pseudopotential with less non-local components, it will be useful to know whether one can use a Al pseudopotential without explicitly carrying dV_d(r). We have therefore generated a series of partly local pseudopotential for Al with only dV_s(r) non-zero, i.e. only requiring one non-local projector. We started by simply taking V_p(r) as local component V^L(r) and just ignoring dV_d(r). There pseudopotentials were tested in a systematic investigation of bulk properties [Ref.M.1]. The results showed, interestingly, that although all such pseudopotentials reproduce very good scattering of s and p states in logarithmic derivative tests, pseudopotentials that have larger r_c give better bulk properties (Table.IV.3.1). We regard this as an indication of the importance of the d-character in Al metal. Since no explicit non-local part for d is used in these Al pseudopotentials, the d-scattering is represented by the local component V^L(r), which is actually the V_p(r) from the 3p state of Al. This V^L(r) is repulsive around r = 0 due to the cancellation effect from the inner 2p shell, which leads to a low electron density at small r and results in a repulsive V_p(r) there to exclude electrons. On the other hand, in the contrary, the 3d component of Al has no cancellation effect and V_d(r) is therefore attractive near r = 0, and this will give significant error in bulk properties involving the 3d character of the electrons. We therefore expect the more repulsive V^L(r) derived from V_p(r) to give worse d-scattering, as shown in Fig.IV.3.4. Moreover, the smaller the r_c is the more repulsive the 2p component will be (Fig.3.5), and hence the worse the result, which is opposite to the common impression that using a small r_c usually keeps a pseudopotential accurate.

To address this problem, I have generated a V_p(r) for Al using Q_c-tuning (Chapter II) to make it as attractive as possible so that it can mimic the shape of V_d(r) , while keeping the scattering of the p-wave correct. This is shown in Fig.IV.3.6 in comparison with the original Al pseudopotential components. The solid state tests [Ref.T.1,M.1] done by D. I. Thomson and N. Marzari showed that this "d-aware" sp-pseudopotential of Al out-performed the best of the original pseudopotentials in giving much more improved structural-critical quantities such as elastic tensor constants C₁₁ C₁₂ and C₄₄, as shown in Table.IV.3.2. The result of this study reveals the role of the d-non-locality of a pseudopotential in the elastic properties of Al fcc metal, and more importantly, it demonstrates how can one generate a reliable pseudopotential with very few non-local components, which reinforces the usefulness of Projector Reduction.

IV.4. Discussion and Conclusion

Discussion

In Section 2 we have applied the Projector Reduction technique on a number of cases to investigate the non-locality of pseduopotentials, in which the cancellation effect is not only used as an insightful classification but also it helps to explain the success of a simple local pseudopotential for Ge. For Ge, all 4s, 4p and 4d valence states are cancelled, yeilding very weak (and hence more similar) V_l(r) corresponding to l=0,1,2, this therefore makes the use of a local pseudopotential for Ge possible. However, one should be careful in using cancellation effect or cancellation theorem [Ref.H.2] in the discussion of the non-locality of a pseudopotential because the effect has more important influences in some types of pseduopotential than others, in other words it depend on the type of the pseudopotential method. We have found that although the cancellation argument can stilled be used in norm-conserving pseudopotential, its predictbility on whether a local norm-conserving pseudopotential can be used for a given element should not be overemphasised. Take Si for example, although both 3s and 3p are cancelled, a satisfactory Projector Reduction on its V_s(r) and V_p(r) is still hard to achieve. It also worth to distiguish the great similarity between the Q_c-tuned V_p(r) and V_d(r) of B and C (Section 2) from the exact identity of V_p(r) and V_d(r) as a consequence of OPW (Orthogonal Plane Wave) pseudopotential method. The pseudisation of OPW type pseudopotential is done by adding back the feature of core states to a wavefunction which is orthogonal to these core states. Since there is no orthogonoal core states for those un-cancelled l components to be added back, the resulting OPW pseudopotentials should all be identical to the true potential. In the other words, there is no pseudising effect at all on the potential of un-cancelled atomic states (if one invert the radial Schrödinger equation by using such atomic wave functions). As for the norm-conserving pseudopotentials, however, valence states are mortified in most cases no matter whether there are underlying core states with the same l. In other words the cancellation theorem predicts the OPW V_p(r) and V_d(r) for B and C should always be identical, but for norm-conserving ones the similar prediction does not apply. It therefore requires a genuine effort to reduce the projectors of a norm-conserving pseudopotential even its valence states have no low lying core states with the same l, which is exactly what happened in the cases presented in Section 2. We are pleased to find that our method works for norm-conserving pseudopotentials. The general limitation of applying the method, as explained in Chapter III, is the r_c of the pseudopotential in a practical application.

The above reduction of non-locality between l=0 and 1 for B, C, N and O has so far been the most successful application of Projector Reduction. It has solved a previous dilemma in our research group, namely how best to generate pseudopotentials for these elemets in KB form. There are several reasons to for and against the inclusion of the d component in such pseudopotentials, but neither was clearly more appropriate than the other. The reasons for not including V_d(r) are : (1) to avoid the extra computing cost (both in CPU and memory), (2) the energies of the d-states for these elements are too high to be important [Ref.W.1], and (3) using a somewhat arbitrary ionised d reference state in the KB form is not always justifiable. On the other hand, the reasons to use V_d(r) are : (1) the contribution from the d-component of Bloch states may be important, (2) the recipe for using (bounded) ionised d-state published in the BHS paper [Ref.B.1] is well established and accepted as a useful approach, and (3) some other reputable group using only V_s(r) and V_p(r) seems to get less convincing results [Ref.N.1]. Fortunately, the success in reducing the pd non-locality of the pseudopotentials of these elements results in a much more satisfactory situation because these pseudopotentials are : (1) extremely fast with a low memory demand (only s is treated non-local, making the potential up to 8 times more efficient), (2) the BHS d-state pseudopotential is used, and (3) no KB form is needed for either d or p components. Equipped with the experiences acquired from these first row elements and the case study of (s-non-local p-local) Al described in Section 3, we have a better understanding and a better handling of the non-local components of a pseudopotential : both are essential for a more accurate strategy of pseudopotential design.

Conclusion

In conclusion, we have demonstrated how to apply the Projector Reduction method on elements in various categories, and have used this to investigate systematically the non-locality of the pseudopotential according to the nature of the element. We have restricted our discussion to non-f elements. A simple argument based on the Free Electron model and the classical scattering picture suggested that, for non-f elements, l=0,1,2 should be sufficient to account for the dominant angular momentum components of the occupied Bloch states. The results of Projector Reduction further show that not all three parts V_s(r), V_p(r) and V_d(r) of the pseudopotential have to be expressed separately always. Therefore the non-locality of the pseudopotential in much cases can be reduced and the numerical efficiency improved. Since the quality of such projector reduced pseudopotentials can always be examined using the standard logarithmic derivative test on the corresponding l-dependent scattering, this strategy makes the use of local or partly-local pseudopotentials more rigorous and systematic.

The case studies on Al, Si and Ge have shown that it is not always appropriate to use a local pseudopotential, particularly for Si among these three. For example the difference between Si and Ge, and the greater appropriateness of a local pseudopotential for the latter can be understood in terms of the cancellation effect as already remarked. From the view point of reproducing the logarithmic derivatives for valence states, we found that a local pseudopotential for Al is not better than that for Si. Thus there is no fundamental reason (from the atomic view point) why it should be easier or better to make the Al pseduopotential fully local than the Si one. We therefore think that a local pseudopotential works better for Al than for Si simply because many applications of Al are less sensitive to those pseudopotential errors caused by insufficient non-locality, in particular in the treatment of V_s(r) and V_p(r). We suggest this is related to the metallic close packed structure of Al which involves less directional effects. However the success of the local pseudopotential for Al breaks down when more directionally sensitive properties are calculated, e.g. the C₄₄ elastic constant and the stacking fault energy. This is consistent with a greater role V_d(r) in such properties and the need of a non-local potential to calculate them.

In this context we have successfully generated a new pseudopotential for Al which only needs a non-local projector for dV_s(r). This was achieved by using Q_c-tuning to generate a p-potential which is attractive in shape so that it mimics V_d(r) and can be chosen as the local part V^L(r). The significant improvement of this Al pseudopotential shows the usefulness of the Projector Reduction technique in reducing the non-locality while keeping a pseudopotential reliable.

The methodology developed in this chapter and Chapter III has allowed us to explore the fundamental problem of the non-locality of a pseudopotential. It also provides a robust procedure that leads to a new generation of pseudopotentials whose non-locality has been designed in a specific way according the need of a given application. This well-controlled non-locality makes a pseudopotential as efficient as possible while keeping control over the important angular momentum components. The approach is equally useful when the pseudopotential is expressed in Kleimann-Bylander form. The ability to adjust and test the non-locality of a pseudopotential systematically represents a further step toward the better understanding and the technical enhancement of generating pseudopotentials for large scale electronic structure calculations.

Acknowledgements

I would like to thank Dr. J-S. Lin for helping with the logarithmic derivative test program, which I used extensively in the current work. Dr R. J. Needs, Dr M.C. Payne and Prof. M.W. Finnis kindly informed me of useful source of information. Thanks are due to N. Marzari and D. I. Thomson for their rigorous tests on the Al pseudopotentials generated by the method described in this chapter. Without those tests being quickly available, the progress of this project would have been slower.

References

[B.1]

G. B. Bachelet, D. R. Hamman, and M. Schluter, Phys. Rev. B 26, 4199 (1982)

[F.1]

M. W. Finnis, private communication

[G.1]

L. Goodwin, R. J. Needs and V. Hiene, Phys. Rev. Lett 60, 2050 (1988)

[H.1]

D. R. Hamann, M. Schluter and C. Chaing, Phys. Rev. Lett 43, 1494 (1979)

[H.2]

V. Heine, Pseudopotential Concept, Solid State Physics Vol.24 (1970)

[H.3]

V. Heine, and R. J. Needs, private communication

[K.1]

R. D. King-Smith, M. C. Payne and J-S. Lin, Phys. Rev. B 44, 13063 (1991)

[K.2]

L. Kleinman and D.M. Bylander, Phys Rev. Lett. 4, 1425 (1978)

[K.3]

G. P. Kerker, J. Phys. C 13, L198 (1980)

[L.1]

J-S. Lin, A. Qteish, M. C. Payne and V. Heine, Phys Rev B 47, 4174 (1993)

[M.1]

N. Mazari, TCM First Year Report (The solid state tests was done mainly by N. Marzari)

[N.1]

R. J. Needs, private communication.

[N.2]

M. Needls, M. C. Payne and J. D. Joannopoulos, Phys. Rev. B 38, 5543 (1998)

[P.1]

M. C. Payne, private communication.

[R.1]

A.M. Rappe, K.M. Rabe, K. Kaxiras and J.D. Joannopoulos, Phys. Rev. B 41, 1227 (1990)

[R.2]

I. J. Robertson, M. C. Payne and V. Heine, Europhys. Lett., 15 (3), 301 (1991)

[S.1]

I. Stich, M.C. Payne, A De Vita, M. J. Gillan and L. J. Clarke, Chem. Phys. Lett. 213, 422 (1993)

[T.1]

D. I. Thomson, TCM First Year Report

[T.2]

N. Troullier and J. L. Martins, Phys. Rev. B43, 1993 (1991)

[W.1]

R. Wentzcovich, private communication.

Table

TABLE.1 Lattice constants and bulk moduli predicted by Al pseudopotentials with different r_c.

(E_cut=150 eV, brodening=3eV)

=======================================================

Potential r_c (a.u.) Q_c/q₃(s) Q_c/q₃(p) a₀ (Å) B (GPa)

=======================================================

Al009 1.6 0.65 0.75 4.15 68.8

Al007 2.2 0.65 0.90 4.12 69.4

Al006 2.2 0.50 0.90 4.12 70.0

Al013 2.4 1.10 1.00 4.08 72.0

-------------------------------------------------------

Expt. - - - 4.05 79.4

-------------------------------------------------------

Al013a 2.4 1.10 1.10 4.02 81.5

=======================================================

TABLE.1 The comparison of bulk properties of fcc metal Al using different Al pseudopotentials

==================================================================

Pseduopotential a₀ (Å) B₀ (GPa) B₀' C₁₁ C₁₂ C₄₄

==================================================================

al.4^a 3.969 79.90 4.82 96.54 54.19 29.10

al2001^b 3.960 83.47 4.51 103.6 51.76 29.60

Al013^c 4.085 71.9 4.69 69.20 55.66 17.80

Al013a^d 4.022 76.7 5.56 103.8 60.8 28.5

Experiment 4.05 79.4 5.15 114.3 61.92 31.62

==================================================================

a. Ref.T.2 (with dV_d(r))

b. Ref.K.3 (with dV_d(r))

c. The original sp only pseudopotential with a less attractive V ^L(r) (without dV_d(r))

d. The specially Q_c-tuned one with a more attractive V ^L(r) (without dV_d(r))

Figures

FIG.IV.2.1(a)

V_l (r) components of the C pseudopotential, only V_p(r) and V_d(r) are shown, the high degree of similarity between them ensures the logarithmic derivative of d-state to be faithfully reproduced by V_p(r) solely, as can be seen from the comparison on Fig. 2.1(b) and 2.1(d). (C021)

FIG.IV.2.1(b)

The logarithmic derivative of p and d-state by the C pseudopotential with its dV_d(r) kept.

FIG.IV.2.1(c)

The logarithmic derivative of p and d-state by the C pseudopotential with its dV_d(r) removed.

FIG.IV.2.2(a)

V_l (r) components of the B pseudopotential, only V_p(r) and V_d(r) are shown. (B001)

FIG.IV.2.2(b)

The logarithmic derivative of p and d-state by the B pseudopotential with its dV_d(r) kept.

FIG.IV.2.2(c)

The logarithmic derivative of p and d-state by the B pseudopotential with its dV_d(r) removed.

FIG.IV.2.3(a)

The p and d components V_p(r) and V_d(r) of the Br pseudopotential, which are Q_c-tuned similar. (Br000)

FIG.IV.2.3(b)

The logarithmic derivative of p and d-states by the Br pseudopotential. (Pseudo : solid line, all-electron : dased line.)

FIG.IV.2.4(a)

The V_s(r) and V_p(r) components of the Fe pseudopotential, they are Q_c-tuned to be very similar. (Fe002)

FIG.IV.2.4(b)

The logarithmic derivative of s and p-state by the Fe pseudopotential with its dV_s(r) and dV_p(r) removed. (Pseudo : solid line, all-electron : dased line.)

FIG.IV.2.5(a)

The V_s(r) and V_p(r) components of the Ge pseudopotential which is to be made local. (Ge010)

FIG.IV.2.5(b)

The logarithmic derivative of s and p-states by the Ge pseudopotential with [0.8V_s(r) + 0.2V_p(r)] chosen as local component V ^L(r), with all non-local parts dV_s(r) and dV_p(r) and dV_d(r) removed, thus this is actually a local Ge pseudopotential.

FIG.IV.2.5(c)

The logarithmic derivative of s and p-states by the same Ge pseudopotential but with the full projectors. A better accuracy of such potential then the local one is expected.

FIG.IV.3.1(a)

The V_s(r) and V_p(r) used to construct the local pseudopotential for Al.

FIG.IV.3.1(b)

The logarithmic derivative of s and p-states by the local Al pseudopotential. (Pseudo : solid line, all-electron : dashed line.)

FIG.IV.3.1(b)

The logarithmic derivative d-state by the local Al pseudopotential. (Pseudo : solid line, all-electron : dashed line.)

FIG.IV.3.2(a)

The V_s(r), V_p(r) and V_d(r) which are used to construct the local Si pseudopotential.

FIG.IV.3.2(b)

The logarithmic derivative of the s and p-states using the local Si pseudopotential. (Pseudo : solid line, all-electron : dashed line.)

FIG.IV.3.2(c)

The d-states logarithmic derivative by the local Ge pseudopotential. (Pseudo : solid line, all-electron : dashed line.)

FIG.IV.3.3(a)

The V_s(r), V_p(r) and V_d(r) used to construct the local pseudopotential for Ge.

FIG.IV.3.3(b)

The logarithmic derivative d-state by the local Ge pseudopotential. (Pseudo : solid line, all-electron : dashed line.)

FIG.IV.3.4

The logarithmic derivatives of d-state by the V^L(r) of Al pseudopotentials with different degree of attractiveness. (All-electron : thick dots, attractive V^L(r) : dashed line, flat V^L(r) : solid line, repulsive V^L(r) : dot-dash.)

FIG.IV.3.5

V_p(r) of Al pseudopotentials with different r_c.

FIG.IV.3.6

The V_p(r) and V_d(r) of a typical Al pseudopotential, here two possible V_p(r) are also shown, the best V_p(r) generated from usual approach is shown in dashed line which is much less attractive then the typical V_d(r) (dot-dash). The "d-aware" V_p(r) in shown in full line, its more attractive feature and its effect to imitate V_d(r) is obvious.