VI

Ideas for Further Research

In the course of the work described in Chapters II to V, various problems have been encountered to which I have given some consideration without resolving them definitively. The present chapter will indicate some of my ideas and results as far as they have got, with thoughts for further research. The discussion is inevitably uneven and incomplete.

The points to be discussed are collected under three headings. Section VI.1 is devoted to various issues connecting to overlap of the pseudo cores of radius r_c. Section VI.2 discusses the effect of Q_c-tuning optimisation on a pseudopotential which is already very soft initially.

Elements in groups I-A and II-A of the periodic table has always presented problems for pseudopotential generation. These include the need for non-linear core correction, difficulty in reducing r_c sufficiently, and others. We need a practical method to generate accurate pseudopotentials in this family, and also a better understanding of the effect of highly excited reference states in the Kleiman-Bylander non-local projector form.

VI.1. Pseudo Core Overlap

The power of ab initio total energy pseudopotential method in understanding the complex electronic structure problems is widely recognised. There are more and more challenging studies carried out involving systems far from the normal crystalline solid state. Due to the wide variety of physical and chemical environments, the proper design and use of pseudopotential has never been so important. In some of these cases we are close to the limitation of pseudopotential approximation. However the overlapping pseudo cores is a typical problem which frequently arises in molecular and high pressure studies. This motivates us to develop better strategies for using pseudopotentials when the pseudo-cores are inevitably overlapping. Note that we are discussing a mathematical point concerning overlap between the spheres of radius r_c, which have nothing to do with the size of the real atomic cores.

There are two scenarios that will appear in our following discussion : If the error comes from the region near r_c then the "Feed Back Loop" effect is important, and therefore the "lowest reliable E_cut" approach should improve the situation. If the error is mainly due to the central region around the origin, the core penetration is significant and hence the "Non-linear Core Correction" should help to correct it. Detailed discussions are presented in the following sections.

Pseudo Cores Overlapping and A Feed Back Loop

It is extremely difficult to avoid pseudo cores overlapping in molecular system such as O₂ and CO. The bond length of O₂ is 1.207 Å and for CO it is 1.128 Å, whereas typical small-core optimised C and O pseudopotentials have pseudo core radii around 1.2 to 1.4 Bohr radius, which will obviously produce overlap. If an even smaller core is chosen, then there is not much left to be optimised and the pseudopotential will be extremely hard. It is therefore not recommended to use 2p pseudopotentials having such a small core.

It is natural to ask the question whether one can simply use overlapped core regions and still get reasonable results. Unfortunately, from the systems tested this seems not to be the case. In those tests we have seem the bond length shorten when E_cut is increased. A heavily overlapped O₂ usually leads to a very short bond length.

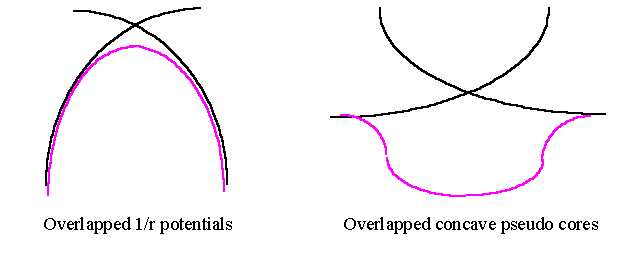
Based on this observation, we have proposed a possible mechanism to explain what might be happening during the testing process and how things start to go wrong. We think that between overlapped pseudopotentials, there is an unphysical feature which comes in when adding up two overlapped pseudopotentials. As shown in the following figures, adding up two Coulombic (convex) potentials leaves only a smooth maximum between two centres. However, adding up two flattened (because of pseudising) attractive concave-shaped pseudopotentials will produce an artificially attractive well in the middle. This attractive well is fairly localised in space and therefore requires higher Fourier components to describe. There will certainly be some amount of charge accumulates in this region, but there may not be very much when the E_cut is low as the attractive well will be numerically smoother (or flatter). When we increased E_cut this part was further revealed, making it to attract more electron density which made the centre of the bond more negative and therefore brought two ions closer. This increased the overlap further and deepened the well, so the entire procedure formed a feed back loop ! This explains why we have seen slow converging of bond length with respect to E_cut. Of course the bond length will finally converge somewhere, but probably at a very very short on incorrect one.

If our suspicion is reasonable, then to correct this error we should not use the highest converged E_cut obtained from a (core-overlapped) molecule test. To address this problem, we proposed a strategy to deal with the over estimated E_cut which gave the bad quantities. The idea is to use the lowest possible E_cut to minimise the possible error that will come from the overlapped region, but it should be high enough for calculating physical properties.

Our strategy is to take the "Lowest Reliable E_cut" from non-overlapping calculations from of that same pseudopotential, and then just stick with it for all the major calculations. By using this lowest-reliable E_cut we de-emphasise the artificial well and therefore minimise the error from the overlapping region, while still providing an E_cut that will satisfy the requirement of electronic structure studies. We know this E_cut is usable because it works for the non-overlapping cases.

Take the CO molecule as an example. In our case both C and O were tested before and we already know that O has the harder pseudopotential. We read from the non-overlapping MgO convergence test that 500eV is the E_cut where the E_tot reaches a sudden drop, which is an indication of the onset of the physical E_cut region. We then use this 500eV for CO. Both ionisation energy and bond length have been looked at and the results turn out to be surprisingly satisfying for the study the chemisorption which this CO was aimed at. We show tests on CO in Tables 1 and 2. The Table 2 is from [Ref.H.1]. Note that the calculation with more heavily overlapped cores has a worse convergence of the bond length, which might be suggesting the effect of the E_cut feed back loop.

Another possible evidence to link core-overlap with the bond length problem is from the tests on CH₃OH and O₂ molecules. Using the same E_cut, different O potentials that gave noticeable different bond lengths for O₂ turned out to be not affecting the CH₃OH tests. This is consistent with the fact that in O₂ we have more serious core over-lapping than in CH₃OH. Some of the tests are shown in Tables 3 and 4, which were done by R. Shah.

If the above analysis of the source of core-overlap error is true, then further correction can be done at the stage of super-cell calculations. We can try to reduce the double counting error by really picking up the double counted region in real space, and avoiding it.

VI.2. Softer Si Pseudopotentials

Although the Si pseudopotential is perhaps the softest one in the periodic table, there are occasions when calculations are needed on a system contains many Si atoms already. It will then be useful to reduce the E_cut as much as possible. The Optimised Pseudopotential method was usually used to treat elements with hard potentials only. In this section we present a case study of using Q_c-tuning to generate Si pseudopotentials with different degrees of optimisation. The Si potentials under study are Si001, Si014 and Si017, whose parameters can be found in Chapter V. A Kerker-type potential Si012 is also included in this study as a comparison. Fig.VI.2.1(a), (b) and (c) compare these pseudopotentials in different aspects.

It is obvious from the convergence plots Fig.VI.2.1(a) that the heavier optimisation, i.e. the smaller Q_c , the more obviously the E_tot converges in successive steps. The Fourier transform plots Fig.VI.2.1(b) reveal the mechanism of how Q_c works on the E_tot/E_cut relation. We can see that in general terms, the main weight of the Fourier components is shifted to lower q when a smaller Q_c is used, as expect from our understanding. It is understandable that the more oscillating the shape is, the more the convergence will proceed in steps as E_cut hits each extremum in turn. Although the convergence of E_tot with respect to E_cut is not the same for all these Si pseudopotentials, the bulk tests done by Dr. R. Perze in the Tables 6, 7 and 8 show that these pseudopotentials all gave very good results when a very high cut-off of 400 eV was used, but the pseudopotentials optimised with smaller Q_c do indeed converge to the correct value more quickly.

As a test application, the 2x1 reconstruction on Si (111) surface was also calculated by Dr. Perez. An interesting aspect was found in the test : although the same Kerker-type Si pseudopotential (see Si012, Chapter V) was used, E_cut = 10 Ryd is necessary to start to simulate dimer bulking correctly, in contrast to the 7 Ryd E_cut reported in the study of 7x7 reconstruction on Si (111) surface [Ref.S.2]. The reason for this may be that the sp hybridisation in these two cases is slightly different. A common Si pseudopotential, such as Si012, has its s potential very much harder than their p potential. It is possible that for a given E_cut the p character is fully converged but the s hasn't. If a physical property is mainly due to p character and less sensitive to the s-feature than the E_cut is sufficient to give a reasonable result. In the other word, if we imagine scanning E_cut from low to high then we will see the more p-related features converges before the more s-related.

In most hard pseudopotentials the Q_c is used mainly to fine-tune the scattering and control the shape. The use of Q_c to improve convergence has been less emphasised because the value of Q_c has been chosen based on an overall consideration of performance, namely accuracy, the possibility of reducing projectors, and core radius. There have not been very many systematic tests of E_tot/E_cut with respect to Q_c. From the case study of optimising Si pseudopotentials presented in this section, we know that even for a soft pseudopotential such as Si, we can still use the Q_c-tuning method to make it softer, and using the E_cut at the first convergence step of E_tot already gives reliable results for bulk properties, which is consistent with the case of Cu reported in Chapter II, in which we found the convergence at the level of 0.1 eV is enough to reproduce bulk properties, instead of 0.01 eV. In the future, it will be useful to have a more systematic investigation on two questions, which are "to what extent can one push down the Q_c for a soft pseudopotential ?" and "what E_cut should be used for a reliable calculation ?".

VI.3. The Special Cases of the I-A and II-A Elements

The reason why we pay special attention to I-A and II-A Group elements is that their atomic ground states have only s valence electrons, which has two negative effects on the pseudopotentials. Firstly, the heavier elements of these Groups have very large atomic radii because of their very loosely bound valence electrons, which makes the procedure of pseudising the wavefunctions under a reasonable r_c extremely difficult. Secondly, for those elements the non-s states will be quite highly excited and therefore very different from solid state configurations. This is likely to cause a problem when Kleinman-Bylander projectors are used because they need to use these excited state as references states. We will discuss these two problems in the following two subsections.

Big Core Problem

The very large atomic radii of the heavy I-A and II-A elements, due to their very loosely bound valence electrons, make pseudopotential generation of them extremely difficult. This is because that the condition for successful pseudisation usually requires a very much larger r_c that leads to a serious pseudo core overlap for most physical applications. One way to cure this problem is to "unfreeze" some of the core electrons and treat them as valence electrons in solid state calculations. By doing so we have much smaller core radii for those potentials, and this strategy also automatically solves another possible problem namely that of core polarisation, which is likely to occur for elements in the category of heavier I-A and II-A elements. Freeing part of the core shell inevitably makes a pseudopotential very hard, and this is the place where our powerful Q_c-tuning Optimisation technique comes in. With that high degree of optimisation, we can make the solid state calculation with pseudopotentials still feasible. This strategy has been used in generating Ca, Sr, Ba (see Chapter V. Ca005, Sr002 and Ba015Rg) and tested for small molecules [Ref.M.1] as well as solids, which give very good results in CaO [Ref.M.2, R.1], and work reasonably in SrO (see Sr002 in Chapter V) and Ba₂NH [Ref.W.1] respectively. It is worth emphasising that in these cases we have Kleinman-Bylander pseudopotential with no reference to any artificial excited state. (More details related to KB form will be discussed in next subsection.).

It will be interesting to ask whether treating some of the core electrons as valence ones is the only way to improve the result of calculations using pseudopotential of I-A and II-A elements. Maybe one can just allow pseudo cores to overlap and will still obtain reasonable results. More tests and comparison on this aspect is need to find the best strategy for generating best pseudopotentials for I-A and II-A elements in the periodic table.

Excited State Problem

For I-A and II-A elements the valence electrons only occupy s-orbitals in the atomic ground states, as already mentioned. This means both the p and d pseudopotentials need to be generated by using excited state configurations. Thus the number of pseudopotential components generated from excited states is larger for this group of elements than typically for other elements. In this section we take Mg as an example to discuss the excited state problem in I-A and II-A Groups.

We have observed that a local Mg potential performs better than a non-local Mg potential generated from the excited states suggested in the BHS paper. This is seen in both MgO (as shown below, and also [Ref.R.1]) and MgCl₂ [Ref.Q.1] calculations. We think the reason for the non-local Mg pseudopotential to be unsatisfactory is due to its using those very artificial excited atomic states as references states in the Kleinman-Bylander non-local projectors. To identify the problem, we have performed a series of MgO tests using similar Mg and O pseudopotentials, both with or without s, p, d non-local components.

The Table 9 gave us the stresses in a MgO cell calculated at E_cut = 450 eV when different Mg and O pseudopotentials are used, with the lattice parameter set equal to the experimental one in all cases. This gives a quicker measure of how well the pseudopotential reproduces the observed lattice constant than actually finding the equilibrium value with each pseudopotential. Clearly the smaller the absolute value of stresses the better, because it means the equilibrium lattice parameter will be closer to the experimental one. From this table we found that the results are worst (corresponds to 5% shorter lattice parameter than experimental result) whenever the Mg has a non-local d-potential, no matter whether the O pseudopotential carries only s and p components or all s, p, d components. The non-local d component in the O, which we have made similar to p one, turn out to be not important. The table also shows that non-local p potential on the Mg is not nearly so damaging, although it also makes the lattice parameter somewhat worse, at least for the tests shown.

Considering the fact that the scattering test of the Mg d-state itself is reasonably good, which means that the potential is correct at least for the configuration used to generate it, we believe that it is the highly excited-states nature in the state in the KB potential that makes the MgO results worse because it is too far away from the d-like states in the solid. Just to use a local potential in these elements seems to be a straight forward idea, at least it works in some systems (Mg in MgO, Na in Na/Si [Ref.M.1]). In the future we should test the same properties of MgO with a Mg pseudopotential generated using the d-component as local so that there is no effect from the KB form of d-part. If the result is better than the one using Mg with the KB for d-component, then we know precisely it is the excited d reference state cause the problem.

In the case of MgO we are now convinced that the error is from the d-potential, but unfortunately d-states do not exist in any core or valence level of the neutral Mg atom, so that we can not take the advantage "un-freezing" a d-shell to avoid excited state.

In the future,

VI.4. Conclusion (Suggested Future works)

In brief, we have discussed various issues of generating, using and testing pseudopotentials in this chapter, they are the problems of core-overlap, using Q_c-tuning for soft pseudopotentials, and problems of big pseudo core and KB projectors related to I-A and II-A group elements in the periodic table.

We have demonstrated that the pseudo-core overlapping is not an absolute disaster which need to be avoided without any compromise. A hand waving argument based on the feed back loop of the degree of overlap and its relation to E_cut has been proposed, which leads to an alternative approach of using the "lowest but still reliable E_cut" in a pseudo-core overlapped calculation. The test results of CO molecule seems to be very promising. The nest step will be to quantify the error caused by using overlapping pseudopotentials. It may be possible to introduce some sort of correction to reduce the error from the undesired situation without making r_c of pseudopotentials very small to avoid overlap, which is obviously very expensive to compute.

In the Section 2 we have applied the Q_c-tuning method described in Chapter II to generate even softer Si pseudopotentials. Successive steps of E_tot convergence with respect to E_cut has been observed, which has a more pronounced effect when a smaller Q_c is set. What can be done next is to establish the optimum condition of using E_cut with respect to Q_c , so that a smaller E_cut can be used. This can be done through systematic tests on the convergence of physical properties with respect to the E_cut .

Two of the major problems we have encountered in generating pseudopotentials are (1) the need to choose a large pseudo core which is larger than the larger than half of the inter-atomic distance, and (2) the difficulty in generate a reliable pseudopotential for atomic states which not occupied in its ground state configuration. Both of these two problems occur in pseudopotentials for I-A and II-A elements, making them more difficult to handle than pseudopotentials of other elements. By taking the advantage of Q_c-tuning Optimisation method, we treated part of core electrons as valence one so that the a smaller r_c can be used, and the resulting pseudopotentials are still soft enough to be handle. It worth to carry out some calculations to compare the performance between normal pseudopotentials with big pseudo-cores and those specially treated with extra valence electrons and smaller pseudo-cores one, thus a better strategy of dealing with a big core pseudopotential can be hopefully be found. As for the excited (reference) states and the (possible) KB form problem, a systematic investigation has been done to identify the source error for the case of Mg pseudopotential. A few more tests (in the future) for more elements to investigate whether or not one need to use certain components in a non-local pseudopotential, such as the one presented in Table. 9, will be most useful.

References

[A.1]

O.K. Andersen, A.V. Postnikov and S. Yu. Savrasov, Mat. Res. Soc. Symp. Proc. Vol. 253, 37 (1992)

[H.1]

P. Hu, D. A. King, M. -H. Lee, S. Crampin and M. C. Payne, submitted to Phys. Rev. B

[K.1]

G. P. Kerker, J. Phys. C 13, L198 (1980)

[L.1]

S.G. Louie, S. Froyen and M.L. Cohen, Phys. Rev. B 26, 1738 (1982)

[M.1]

V. Milman, M.C. Payne, V. Hiene, R.J. Needs, J.S. Lin and M-H. Lee, Phys. Rev. Lett. 297, 3971 (1993)

[M.2]

V. Milman, private communication.

[Q.1]

A. Qteish, private communication.

[R.1]

K. Refson, private communication.

[S.1]

R. Shah, TCM preprint & private communication.

[S.2]

I. Stich, M. C. Payne, R. D. King-Smith, J.-S. Lin, and L. J. Clarke, Phys. Rev. Lett. 68, 1351 (1992)

[W.1]

B. Winkler, V. Milman, M-H. Lee and M.C. Payne, submitted

Tables

TABLE.1. Test of the bond length of the CO molecule

using LDA and pseudopotentials C009 (r_c=1.2 a.u.),

C019 (r_c=1.0 a.u.), O027 (r_c=1.4 a.u.).

=================================

E_cut C009/O027 C019/O027

(eV) bond length error bond length error

=================================

400 +3.68% -

500 +0.01% +1.06%

600 -1.43% -1.05%

700 -1.76% -1.05%

800 -1.80% -0.98%

=================================

TABLE.2. Convergence tests of CO using

LDA and two sets of pseudopotentials.

===========================

E_cut C009/O027 C019/O027

(eV) E_tot (eV) E_tot (eV)

===========================

400 -577.9095286 -

500 -584.2689334 -583.4517404

600 -587.1691199 -586.6544886

700 -588.3228353 -588.0217869

800 -588.7314478 -588.5846829

===========================

TABLE.3. CO properties (using pseudopotentials C009 and O027 at E_cut = 500eV)

==============================================================

bond length (Å) error vibrational frequency (cm^-1 ) error

==============================================================

LDA 1.1281 -0.02% 2167 1.1%

GGA 1.1257 -0.23% 2206 2.9%

----------------------------------------------------------------------------------------------------

Expt. 1.1283 - 2143 -

==============================================================

TABLE.4. Results of fully relaxed calculations of

methanol molecule using different E_cut , using the LDA

with pseudopotentials C009 and O027.

========================================

E_cut E_tot C-H C-O O-H angle angle

(eV) (eV) (Å) (Å) (Å) C-O-H H-C-O

========================================

450 -644.939 1.113 1.400 1.009 107.3 110.8

500 -647.576 1.109 1.411 0.992 107.2 110.7

550 -649.422 1.108 1.410 0.979 107.5 110.6

600 -650.716 1.108 1.409 0.972 107.8 110.6

650 -651.498 1.108 1.404 0.969 108.4 110.5

700 -652.023 1.108 1.403 0.968 109.2 110.5

------------------------------------------------------------------

Expt. --- 1.09 1.42 0.96 107.2 108.0

========================================

TABLE.5. Results of fully relaxed calculations of

methanol molecule using different E_cut and using GGA

with pseudopotentials C009 and O027.

========================================

E_cut E_tot C-H C-O O-H angle angle

(eV) (eV) (Å) (Å) (Å) C-O-H H-C-O

========================================

450 -649.620 1.103 1.408 1.003 107.2 110.5

500 -652.296 1.099 1.419 0.984 107.2 110.5

550 -654.163 1.097 1.418 0.972 107.6 110.5

600 -655.465 1.097 1.418 0.964 108.3 110.4

650 -656.249 1.097 1.413 0.961 108.6 110.4

700 -656.777 1.097 1.410 0.961 108.8 110.4

----------------------------------------------------------------

Expt. --- 1.09 1.42 0.96 107.2 108.0

========================================

TABLE.6. Lattice parameter (Å) test for Si (diamond structure)

====================================================================

E_cut(eV) Si012 Si001 Si014 Si017 Experiment

--------------------------------------------------------------------

82 - 5.41386 5.42482 5.42723 5.429

96 - 5.43734 5.44538 5.44527 5.429

100 5.38754 5.44349 - - 5.429

125 - 5.45656 5.45701 5.45090 5.429

150 5.41644 5.46373 5.46105 5.45243 5.429

175 - 5.46613 5.46228 5.45258 5.429

200 5.40306 5.46556 5.46190 5.45330 5.429

300 5.39118 5.46478 5.45763 - 5.429

400 5.38618 5.46520 5.46247 5.45824 5.429

====================================================================

TABLE.7. Bulk modulus (GPa) tests for Si (diamond structure)

====================================================================

E_cut(eV) Si012 Si001 Si014 Si017 Experiment

--------------------------------------------------------------------

82 - 0.95158 0.90941 0.90060 0.99

96 - 0.91392 0.89660 0.90426 0.99

100 0.92465 0.84430 - - 0.99

125 - 0.92255 0.91851 0.92335 0.99

150 0.94260 0.89955 0.90196 0.91990 0.99

175 - 0.90321 0.89641 0.91901 0.99

200 0.99042 0.91040 0.90876 0.91863 0.99

300 1.01318 0.91840 1.00568 - 0.99

400 0.96332 0.91035 0.90969 0.91068 0.99

====================================================================

TABLE.8. dB/dP tests for Si (diamond structure)

====================================================================

E_cut(eV) Si012 Si001 Si014 Si017 Experiment

--------------------------------------------------------------------

82 - 6.40779 6.15718 5.98730 4.23

96 - 5.39034 5.03432 4.79465 4.23

100 7.06836 6.30272 - - 4.23

125 - 4.46634 4.20827 4.26344 4.23

150 4.80548 4.38808 4.24563 4.17850 4.23

175 - 4.20176 4.30937 4.17551 4.23

200 3.82422 4.07522 4.08639 4.10915 4.23

300 2.33116 3.94766 2.71731 - 4.23

400 4.16637 4.06751 4.08091 4.09504 4.23

====================================================================

TABLE.9. Tests of MgO crystal (at E_cut = 450 eV) using different Mg and O

pseudopotentials. The non-local components carried by the pseudopotential

is indicated in the ( ) next to the symbols of elements. The column fort.11

indicates the actual pseudopotential data files used.

============================================================================

Mg O E_total sig_xx sig_yy sig_zz fort.11

----------------------------------------------------------------------------

Mg(s) O(spd) -1818.4653461 0.047905 0.043678 0.051855 Mg006 O020

Mg(spd) O(spd) -1822.1352518 0.169718 0.173849 0.167937 Mg007 O020

Mg(sp) O(spd) -1819.0876292 0.064164 0.059863 0.066161 Mg007sp O020

Mg(sd) O(spd) -1821.8125848 0.164425 0.161849 0.167122 Mg007sd O020

Mg(s) O(spd) -1818.7248693 0.056392 0.052678 0.059353 Mg007s O020a

Mg(s) O(spd) -1814.0010265 0.036187 0.034960 0.037841 Mg006 O020a

Mg(s) O(sp) -1813.4972199 0.018690 0.017259 0.020274 Mg006 O020asp

Mg(sp) O(sp) -1814.1255619 0.034687 0.033260 0.035264 Mg007sp O020asp

Mg(spd) O(sp) -1817.2512260 0.143403 0.142444 0.144053 Mg007 O020asp

============================================================================

Figure Captions

FIG.VI.2.1(a)

E_tot/E_cut convergence tests of the Si pseudopotentials with different value of Q_c.

FIG.VI.2.1(b)

Comparison of the Fourier transforms of the V_s(r) of the Si pseudopotentials generated with different Q_c.

FIG.VI.2.1(c)

The real space radial pseudo s-wave functions R(r) (i.e. rY(r) ) for Si generated with different Q_c.