VII

The Origin of Disorder in g-Al₂O₃

VII.1 Introduction

The purpose of present work is to use computer simulation to understand better the structure of g-Al₂O₃ , in particular its disordered nature.

It is widely accepted that g-Al₂O₃ has a spinel-like structure because the powder X-Ray peaks resemble those of real spinel. There are three features of importance which are clear from the data. A standard spinel primitive unit cell is cubic having 32 oxygen atoms forming fcc structure, with half of all octahedral (Oh) and 1/4 of tetrahedral (T) interstitial sites regularly occupied by cations. Thus the first and second features are that the oxygens have an fcc packing and that the Al atoms are distributed on both Oh and T sites. The structure of g-Al₂O₃ contrasts with that of a-Al₂O₃ in which the oxygens from an hcp structure and the Al are only in Oh sites and well ordered. The evidence for the occupation of both Oh and T sites by Al ions in g-Al₂O₃ comes from IR and Raman vibrational spectra which are sensitive to the local atomic structure. The third point is that there is a substantial degree of disorder, within the spinel-like short and medium range order. This is indicated by the broadening of the X-ray powder diffraction peaks. It also follows form the fact that the spinel unit cell with 32 oxygen ions requires 24 cations, but Al₂O₃ correspond only to Al_21.33O₃₂. Indeed this may be the cause of the disorder because the strong Al³⁺-Al³⁺ repulsion would give a substantially different Al distribution, not just a few vacancies in the spinel structure.

The main questions are : why are both T and Oh sites occupied in g-Al₂O₃ compared with only Oh sites in a-Al₂O₃ when the underlying oxygen structures are so similar, namely fcc and hcp ? Is the occupation of T sites by Al stable in fcc framework ? Or do they just reflect the structure that g-Al₂O₃ inherited from its parent material and would they finally transform into Oh sites ? Even given the fact that both T and Oh sites are occupied, why are they disordered in g-Al₂O₃ ?

Ab initio calculations, by which we mean solving the Schrödinger equation for the whole system, are used in the present study. The reason is that there has been a bad experience in our research group : we have seen slightly different empirical shell models, both fitted to structures and dielectric data, giving substantially different results for the energy difference between Al on T and Oh sites. Therefore an ab initio approach is necessary because in g-Al₂O₃ the occupation of both Oh and T sites by Al ions appears to be a crucial aspect of its structure. However, the disordered/non-stoichiometric nature of g-Al₂O₃ makes a full super-cell ab initio calculation impractical. For example, it would require 3 times the spinel unitcell to have an integer number of Al ions in a supercell. With such a large supercell of 160 atoms, or similar sized cell, it would be too expensive to perform many calculations with the Al ions in different positions to find the ground state.

Since an investigation of g-Al₂O₃ by complete ab initio set of calculations is impossible, we use a 3-step approach instead. The idea is that we can represent the total energy of the system E in terms of a model Hamiltonian to give the energy expression in the form

(1.1) E = E₀ + (m/2) (N_Oh - N_T) + S J_ij h_i h_j

in which E₀ is the energy constant, m is the chemical potential energy difference of one Al ion on an Oh site rather than a T site, N_Oh and N_T are the numbers of Al on Oh and T sites, and h_i is equal to unity when site {i} is occupied and zero when empty. The J_ij is the pair-wise interaction between Al atoms on site i and j, including both Oh and T type sites. We have used a simplified form of this model Hamiltonian in our study, which will be discussed later in Section 4. The reasons to introduce it here in the form of (1.1) is that it high-lights assumption that the interaction is pair-wise as shown by the term S J_ij h_i h_j. With this from of model Hamiltonian, we carry out the following three steps : (1) We perform 10 ab initio calculations on a sufficiently small cell to obtain the 10 energies for 10 different configurations of the Al atoms. (2) We fit the parameters E₀, m, and J_ij in the model Hamiltonian to the 10 ab initio energies. (3) We then do larger scale simulations based on the fitted Hamiltonian to find the ground state distribution of Al atoms in g-Al₂O₃ (and a-Al₂O₃ for comparison).

We found that the large scale simulations (step 3 above) reproduced the fact that the Al atoms only occupy Oh sites in a-Al₂O₃. They also predicted a N_Oh : N_T ratio around 73% : 27% for the Oh and T cation distribution in g-Al₂O₃, which was later confirmed by solid state NMR measurements (giving 70% : 30%) done by colleagues in Chemistry Department at our suggestion. These two quantitative successes of model (1.1) support the belief that the approximations made in the various steps of our computational study fulfil the accuracy needed to address the central question of this chapter, namely the origin of disorder in g-Al₂O₃. The simulations of g-Al₂O₃ in fact always resulted in similar disordered structures. By comparing the simulatation results for both a (hcp) and g (fcc) alumina based on the same model Hamiltonian, we show that the differences between them are due to the underlying geometry of the oxygen frameworks. The methodology we have established not only provides an insight into the fundamental difference between the a and g phases of Al₂O₃ but also the structure and stability of the Al distribution in the "weakly ordered" material g-Al₂O₃.

In the following sections of this chapter, we will mention some background information on g-Al₂O₃ in Section 2. In Section 3 the details of the ab initio calculations will be given and, in Section 4 the construction and fitting of the model Hamiltonian. Section 5 consists of the results from the simulations and corresponding NMR measurements. We will discuss what we have learnt in Section 6 and draw smme brief conclusions. Finally in Section 7 some possible plans for future studies will be very briefly mentioned which provide a wider scope for our interest in g-Al₂O₃.

VII.2 Background Experimental Information

Before starting our analysis in the next section, we review briefly in this section the reasons why g-Al₂O₃ is interesting, which, in fact, motivate our current and future research on this material. We will also mention some experimental facts that are important for our computational investigation or the understanding of this material.

The present study was initiated by Dr. W. Macrodt when he was at ICI. g-Al₂O₃ is important in the chemical industry as a catalyst support and, less frequently, as a catalyst itself. It is a good catalyst support because being a fine powder it has an enormously large effective surface area. Made from very fine particles (microcrystals), it becomes a highly porous solid when compressed and treated. With a very uniform distribution of microcrystal size, the porous solid has a fairly uniform width of channels, which makes the supported catalytic processes size-selective. The catalytic function of pure g-Al₂O₃ itself comes from the formation of catalytic centres on its surface in the presence of a solvent. Even when g-Al₂O₃ is used as a support, people believe that the substrates/reactants will first diffuse on its surface before the catalytic reaction takes place : therefore in that way g-Al₂O₃ also chemically takes parts in the catalytic reaction. We understand that it is also used in paints and in explosives.

We now turn to the background information relevant to the present study. Firstly, g-Al₂O₃ appears easily in many kinds of process involved in the formation of alumina such as the dehydration of AlOOH [Ref.G.1] and the MBE growth of alumina films [Ref.C.2] as an intermediate step, finally leading to the most stable a (corundum) form after annealing. Thus one might expect g-Al₂O₃ to have a lower nucleation energy cost than that of a-Al₂O₃, and it would be interesting to know why. (Is the surface energy lower than that of a-Al₂O₃, or is it a volume effect ?) It was only recently that single-crystal g-Al₂O₃ has been claimed to have been successfully prepared by MOMBE growth on a specially selected substrate [Ref.I.1]. Such a highly sophisticated way for single-crystal preparation, together with the long term puzzle of the difficulty in growing bigger single crystals using industrial methods, high-lights the interesting nature of the crystallinity of g-Al₂O₃.

Secondly, the material exists almost exclusively as micro-crystals, as seen under the Transmintion Electron Microscope (TEM) [Ref.R.1]. The fine particles of g-Al₂O₃ are shown to be nearly hexagonal-shaped platelets. The size of individual small grains is typically a diameter of 10-20 nm and thickness less than 5 nm. Under High Resolution TEM (HRTEM) [Ref.R.1], which probes the local structure at atomic resolution, regular atomic textures and clear facets not only provide the evidence of the crystallinity of g-Al₂O₃ but also allow one to measure the ratio of atomic layer spacing along different lateral directions. Tn this way the Miller Indices of the surfaces of the crystallites normal to electron beam can be determined. This analysis suggests that the preferentially exposed surface of g-Al₂O₃ is [110], which will be an interesting point to study computationally in the future.

Thirdly, it is often quoted that g-Al₂O₃ has a "defective cubic spinel structure" with lattice parameter a₀ = 7.92 Å. [Ref.C.2], as suggested by powder X-ray diffraction. The fact that it has an fcc oxygen framework is widely accepted. We will use these facts (fcc and a₀) to construct the appropriate supercell for our ab initio calculations. Although basically crystalline, there is also an element of disorder in g-Al₂O₃ as seen from the width of Bragg peaks in powder X-ray pattern. The oxygen lattice looks nearly perfect whereas the peaks from the Al atoms appear broader. Our own estimation (unpublished) suggests that the medium range order of the oxygen structure has a with correlation length extending 10 fcc lattice cells or more, whereas the Al peaks are 3 times broader so they have a short range order extending to about 3 fcc cells. Some X-ray crystallographers describe g-Al₂O₃ as "Weakly Ordered" [Ref.S.2] due to the existence of internal disorder within the overall crystalline order in this material. The link between cation disorder in g-Al₂O₃ and its micro-crystalline nature will be another interesting aspect for us to investigate in the future.

Fourthly, the existence of both Oh and T coordinated Al in g-Al₂O₃ is shown by IR and Raman spectroscopies [Ref.C.1] which are sensitive to the symmetry of the local environment of the Al atoms because they detect the allowed transitions between different vibrational modes according to their respective section rules. Analysing both the numbers of IR and Raman active modes of Al-O vibration, experimentalists have shown that their results are consistent with the assumption that modes with Oh-coordinated AlO₆ and T-coordinated AlO₄ local symmetry both contribute to what has been measured. The IR and Raman data therefore support the co-existence of T-site and Oh-site occupation by Al in g-Al₂O₃.

Fifthly, directly monitoring the phase transition process by in-situ TEM [Ref.S.3] enables one to measure the growth rate of g the phase from the amorphous material from video-records of the speed of the boundary between two phases, giving estimated activation energies of 1.6 eV (for T < 750C) and 7.8 eV (for T > 750C) if the simple assumption of a thermally activated process is valid. In another work, activation energies for bulk diffusion of O and Al in a-Al₂O₃ were reported to be 6.6 eV and 5.5 eV respectively, and an activation energy of transformation from a-Al₂O₃ to g-Al₂O₃ of about 3.6 eV. Although not rigorously consistent with each others, these data do provide the order of magnitude of the energies involved in these processes, which we will later find comparable with our computational results.

In conclusion, the picture of g-Al₂O₃ we have is that it consists of micro-crystals with quite good crystallinity of the fcc oxygen lattice. The Al atoms are distributed in a similar way to the cations in spinel structure, occupying both Oh and T sites, but with considerable disorder. Further evidence of the disorder/inhomogeneity of the cation distribution in alumina comes from the asymmetric tunnelling experiments, which suggest that inhomogeneous distribution of Al in aluminium-oxide is responsible for an asymmetrical current-voltage characteristics.

VII.3 Configuration Energies from First Principles Calculations

The interaction between atoms in a complex solid contains many different effects, and the local chemical environment can also be very different even for the same kind of element. Thus empirical interatomic potentials which have been fitted from limited experimental data, have limited capability for describing a system in such a situation. To have a more appropriate starting point we take the ab initio approach, which is used first to understand the characteristics of our system. In practice we make the ab initio calculations to evaluate the total energies of a chosen set of configurations, and then use these in Section 4 to determine the parameters in the model Hamiltonian.

Before embarking on the ab initio calculations, we give first a more detailed critique of the empirical interatomic potentials and our reason for rejecting them, The most sophisticated of the empirical potentials is the shell model in which an atom or ion is modelled by an electrostatically changed core, surrounded by a moveable shell (also charged) connected by a spring to the core and interacting with the shell of neighbouring atoms [Ref.C.3,D.1], The parameters are determined by fitting to a range of crystal structures including their lattice constants, some elastic constants and some dielectric constants. In Professor Volker Heine's opinion, attempts to model oxides as purely ionic materials have often led to inconsistencies [Ref H.1]. Their bonding involves a considerable degree of covalency, as evidenced for example by the bond bending terms at Al (and Si) atoms needed in modelling tetrahedral framework alumino-silicates structures (Ref. used by Thaya). In particaular the covalency effect will differ between Al in Oh and T environments and we therefore expect empirical shell models to be unreliable in representing the energy difference between them. This is crucial for the present study because the Oh and T energy difference is one of the key features in understanding g-Al₂O₃. Indeed in another research project (done by S. Padlewski) involving energy difference between Oh and T Al in mullite, it was found that the results were very sensitive to the empirical potential model used and one reputable parameterisation gave complete nonsense (unpublished !). The point is that these shell model potentials have been fitted to structures and elastic properties, with no information in the database about the energy difference between Al in Oh and T sites. Such failure is not uncommon when using empirical interatomic potentials well outside the type of situation included in the data base to which they have been fitted. However, our research group has been associated with ab initio total energy calculation for solids since near their inception about 15 years ago and we know of no case where a calculation by a reputable group world-wide has had to be filed in the waste paper bin (V. Heine, private communication), in contrast to the simulation with emperical potentials.

In an ab initio calculation, a unit cell is chosen as large as needed or computationally possible to model a complicated process or structure, in our case different configurations of Al in Oh and T sites, which is repeated periodically over the entire space. In such a way, the so-called supercell geometry is used to represent an infinite solid. The Schrödinger equation is the solved for all the valance electrons in the whole system which provide the interatomic bonding. We use the total energy package CASTEP to perform the ab initio calculations [Ref.P.1]. The formalism is based on Kohn-Sham Scheme of Density Functional Theory (DFT), a special represtation of quantum mechanics, with the Local Density Approximation (LDA) for complicated exchange-correlation energy, which come from the many-body effect of interacting electrons. We expand wavefunctions in terms of planewaves which is convenient for handling the periodic boundary conditions. In stead of true potentials for the ions, pseudopotentials are used so that only the valence electrons are treated explicitly in the numerical procedure. At the same time the highly oscillatory part of the wavefunctions within the ion core regions is smoothed away, which reduces enormously the number of planewaves needed to express these wavefunctions. Using pseudopotentials therefore makes the expensive computing affordable. In this regard, an important aspect of CASTEP is that it directly minimises the total energy without diagonalising the one-electron Hamiltonian. For a given ionic configuration, the electronic ground state can be found, its energy calculated, and forces on each ion evaluated. The ions can then be moved, or relaxed, to the positions such that the system reaches its (stable or metastable) total energy minimum of both ionic and electronic structures. Thus our ab initio calculations are static ones, effectively at zero degree Kelvin.

The preparation of ab initio calculations involves generating pseudopotentials, choosing the unit cell geometry and constructing the initial ionic positions for each set of configurations of the Al atoms. Qc-tuned optimised pseudopotentials of Al and O are used, including for Al the use of the techniques developed in Chapter IV for approximating the higher d component of the pseudopotential in terms of the p-potential. Also the O pseudopotential was optimised with a big core-radius (1.8 a.u) to take advantage of the negatively charged nature of oxygen ion in an oxide system for and thus reduce further the number of planewaves needed.

To generate the ab initio database for our study, we used an orthorhombic unit cell with a = 5.599 Å, b = 4.849 Å, c = 6.857 Å, a = b = g = 90^o, containing 12 oxygen atoms in the fcc structrues and 8 aluminium atoms. This cell dimensions have been set to match the experimentally observed atomic spacing of g-Al₂O₃ with the lattice vectors a and b span the basel plane and c pointing along the direction of the conventional ABCABC stacking sequence of an fcc strcture. The 10 different sets of Al configurations are carefully chosen with the number Al atoms occupying Oh sites varying in the whole range of possibilities from 0 to 8. We have checked these input sets to make sure that these initial configurations contain various types of Al-Al pairs and distances to represent the J_ij in Equation (1.1) well. It is important to mention that the size of the unit cell covers the second nearest Oh-Oh and T-T sites, which should be sufficient to cover the major effects of pair-wise Al-Al interaction.

Results of ab initio calculations with both fully (all ions) relaxed and partly (Al only) relaxed were obtained. From these results we noticed that the relaxation of Al positions are large, leaving the Al ions well spread out among the interstitial sites. Some of them had even hopped away from their initial input sites during the relaxation, which indicates the strong electrostatic nature of the Al-Al repulsion. The relaxed oxygen framework still has a distorted fcc geometry. We also note that it is computationally much more expensive to relax the oxygen position, which can be rationalised from the fact that the electrons in our system are mainly around the oxygen ions, so that moving an oxygen ion creates a much larger disturbance to the electronic structure than moving Al. Thus the energies of the 10 configurations used to fit our model Hamiltonian (1.1) only have the Al ions relaxed, keeping the oxygens exactly in the fcc structure. These 10 different initial configurations relaxed into only 9 distinguishable sets because two of them relaxed into the same final configuration. Since we want to explore the energies of the system near its ground state instead of highly unstable configurations, we are happy to see that some ab initio calculations converged into the same structure. To get a feeling for these results, we present two typical sets of Al-only relaxed configurations in Table.3.1. From an analysis of the Al-O distances of a given Al to its neighbouring oxygen ions, we immediately know whether an Al ion is in Oh or T site. It is also worth mentioning that the Al relaxation in Oh sites often results 3 short and 3 long Al-O bonds. The situation for Al to form 1 long and 3 short Al-O bonds in a T site is less frequent but it does happen sometimes. The further analysis of the ionic positions and the total energies will be done in the next section in more detail.

[Table.3.1]

Distances of Al ions to its first 10 nearest oxygen neighnours (in Angs.). We used this information to

identify whether an Al ion is in Oh or T sites, also note that the strong relaxation of Al positions in

Oh and T sites with tendency to form 3 short bonds.

Case 1 (ab initio No.3)

Oxygen neighbour Al(1) Al(2) Al(3) Al(4) Al(5) Al(6) Al(7) Al(8)

1-th O neighbor 1.65 1.74 1.72 1.76 1.70 1.78 1.81 1.75

2-th O neighbor 1.71 1.79 1.74 1.77 1.70 1.79 1.81 1.78

3-th O neighbor 1.74 1.98 1.76 1.78 1.71 1.96 1.84 1.84

4-th O neighbor 1.76 2.02 2.27 2.23 1.72 2.03 2.14 2.17

5-th O neighbor 3.22 2.19 2.28 2.23 3.26 2.18 2.17 2.21

6-th O neighbor 3.23 2.22 2.30 2.24 3.27 2.19 2.17 2.23

7-th O neighbor 3.23 3.16 2.94 3.02 3.27 3.18 3.13 3.07

8-th O neighbor 3.26 3.19 3.27 3.30 3.27 3.22 3.31 3.27

9-th O neighbor 3.26 3.40 3.29 3.31 3.28 3.41 3.35 3.33

0-th O neighbor 3.27 3.43 3.32 3.32 3.28 3.42 3.35 3.36

Occupation Type T Oh Oh Oh T Oh Oh Oh

Case 2 (ab initio No.9)

Oxygen neighbour Al(1) Al(2) Al(3) Al(4) Al(5) Al(6) Al(7) Al(8)

1-th O neighbor 1.60 1.62 1.67 1.63 1.65 1.66 1.70 1.69

2-th O neighbor 1.63 1.63 1.68 1.72 1.68 1.69 1.71 1.71

3-th O neighbor 1.65 1.80 1.73 1.72 1.70 1.72 1.74 1.72

4-th O neighbor 2.07 1.82 1.76 1.78 1.82 1.79 2.32 2.35

5-th O neighbor 2.95 3.13 3.21 3.20 3.16 3.20 2.34 2.35

6-th O neighbor 2.96 3.14 3.24 3.20 3.18 3.21 2.35 2.37

7-th O neighbor 2.98 3.22 3.24 3.23 3.19 3.23 2.87 2.84

8-th O neighbor 3.21 3.22 3.24 3.24 3.23 3.24 3.26 3.26

9-th O neighbor 3.23 3.24 3.28 3.25 3.26 3.27 3.28 3.27

10-th O neighbor 3.26 3.25 3.28 3.26 3.29 3.29 3.30 3.29

Occupation Type T T T T T T Oh Oh

VII.4 The Model Hamiltonian

VII.4.1 Constructing a Simplified Model Hamilton

An efficient Hamiltonian of the type of (1.1) is important for us so that its parameters can be determined by using the least possible numbers of configurations (and total energies) obtained from ab initio calculations. The form of the model Hamiltonian we shall use is based on such practical consideration, and to achieve it we have made three essential further simplifications of the Hamiltonian as the follows :

(1) The same interaction J_ij is shared by Al ions in both Oh and T sites, which greatly reduces the number of parameters in our model Hamiltonian because it is not necessary to distinguish between Oh-Oh, Oh-T and T-T interactions.

(2) The J_ij is assumed to be just a function of the distances between Al ions, using the actual relaxed r_ij distance between them instead of the site labelling (i,j).

We therefore write J_ij = J(r_ij). By doing this we further reduce the number of parameter needed in the Hamiltonian because we have avoided the complication of site labelling in a distorted/relaxed system.

(3) To avoid building in an unwarranted assumption about the form of the function J(r_ij), we represent it by a series of steps covering the ranges 2.6 ± 0.2 Å, 3.0 ± 0.2 Å, ... etc. This helps to reduce the number of parameters further. The partitioning of the distance into different ranges can be adjusted to match the accuracy required.

Our chosen simplifications of the model Hamiltonian may be justified to some extend by analysing the ab initio results. In particular there seems to be sufficient space for the Al ions to relax away from the centres of both Oh and T cages.

This indicates that the radius of the Al ion is sufficiently small not to create large volume strains in either Oh or T sites : such volume strains, if present, would have given substantial long range interactions. A significant volume strain would presumably be larger for the tetrahedral cage then for the octahedral one, thus making it necessary to distinguish between Oh and T sites. The relaxation of the Al inside the tetrahedral or octahedral cage of oxygen ions also shows that a pure site labelling i,j for the interaction J_ij would be extremely complicated because it would in principle have to take into account the displacement at each site. The fact that an Al ion hopped to a neighbouring site away from one another during the relaxation when two Al ion were close together suggested that their interaction is mainly electrostatic, which gives some further justification to not distinguishing between Oh and T site.

With these simplifications we can re-write our model Hamiltonian (1.1) explicitly , for a given cation configuration, as:

(4.1)

where r_m is the midpoints 2.6 Å, 3.0 Å, ... representing the ranges 2.6 ± 0.2 Å, 3.0 ± 0.2 Å ... chosen to partition the Al-Al distances and n(r_m) the number of pairs falling in that range with interaction J(r_m). We have also transformed slightly the terms involving m, using the fact that the total number of Al atoms N_Oh+ N_T in a given simulation is constant, which also gives E₀' in (4.,1) slightly different from E₀ in (1.1). The eight parameters E₀' , m and (six) J(r_m) in (4.1) are determined from the ab initio calculations by the procedure described in the next section.

The reduction of the model Hamiltonian to eight parameters clearly minimises the number of ab initio calculations needed to fit them.

VII.4.2 Determine The Parameters in Model Hamiltonian

The method we used was to fit the eight parameters uniquely to eight of ab initio energies, omitting one of the nine energies in turn. In two cases this gave absured results which we neglected (Table 4.2), leaving the seven fits also listed in Table 4.2. There are very large differences between them and we also show the average of the seven fits, giving the parameters used in the subsequent simulations with their standard deviations.

[Table.4.1]

Fitted parameters of model Hamiltonian (4.1)

Parameters (eV) m J(2.6) J(3.0) J(3.4) J(3.8) J(4.2) J(4.6) E₀'

Fit 1 -2.8 -2.6 0.2 -1.0 -0.7 -0.5 -0.7 -5566.2

Fit 2 -1.8 -0.1 -0.3 -0.6 -0.6 -0.4 -0.4 -5582.4

Fit 3 -0.1 1.6 0.4 0.0 0.1 -0.2 -0.1 -5623.3

Fit 4 -0.3 -1.3 -0.7 -0.5 0.0 -1.1 -0.3 -5583.6

Fit 5 -1.4 5.5 4.6 3.5 2.2 1.1 0.5 -5768.3

Fit 6 -1.9 1.9 2.1 1.0 0.8 -0.6 -0.3 -5652.8

Fit 7 -0.5 -1.1 -1.3 -1.7 -1.3 -0.8 -0.2 -5553.7

Average -1.26 0.56 0.71 0.10 0.07 -0.35 -0.21 -5619.04

s 0.92 2.50 1.86 1.59 1.07 0.65 0.34 68.80

Discarded -15.7 43.0 37.8 21.8 13.9 1.2 -4.8 -6515.1

Discarded 7.8 -6.0 -3.1 -6.3 3.4 2.7 1.9 -5621.3

Again we make the point, firstly, that the results seems to be sufficient for our limited purpose of understanding of the structure of g-Al₂O₃ as show below. Secondly the ab initio calculations are computationally very expensive and we are near the limit of what is feasible with moderate resources.

We note from the table that the chemical potential difference m comes out negative i.e., the Oh site is favoured over the T one, as expected We also see from the table that the Al-Al interaction (electrostatic energy) is comparable with the chemical potential difference of an Al in Oh site and in Td site, which is important because it means the Al-Al interaction may sometimes overcome the chemical potential m to favour having an Al ion in a T site rather than an Oh site. We are also happy to see that the Al-Al interaction is reasonable long (medium) ranged because otherwise there is no way for the Al ions to distinguish the fcc and hcp structures because of their similar local environments of the Oh and T sites.

We also note that the stanard deviation in the average fit is larger for small Al-Al distances, but we are actually not too worried about that because it is fairly clear from the relaxed structures, e.g. from the information in Table 4.1, that the Al ions are highly repulsive to one another, so that at least the sign must be positive, larger error corresponding to this large repulsion is unlikely to change the behaviour of the Hamiltonian qualitatively. We will also see in the Sections 4 that the detail profile of the interaction play a less important role in the difference between a and g phases of Al₂O₃, and that our fit of interaction, although not very well, is already sufficient to reveal the main physical feature of the systems.

When the fitted model Hamiltonian (4.1) is used in a simulation, we have already cut-off the effect of interaction longer than 4.8 Å. because of the definition of (4.1). As for the interaction ranges between 0 and 2.4 Å, we will assign an infinity (or computationally, extremely large) repulsion to represent the fact that having two Al ions such close is energetically highly unfavourable, since there is no one case in our ab initio calculations that a relaxed Al-Al pair have a distance smaller than 2.4 Å, even though there initial conditions do allow that.

VII.5 Simulation of Structures and Comparison with Experiments

Computer simulations based on the fitted model Hamiltonian (4.1) can now be used to investigate many properties of g-Al₂O₃ such as the nature of the ground state, including short range and long range order, etc., on a much larger scale than can be achieved ab initio. The planned simulations are partly completed and we present here the results. We will attempt understand from them the disordered nature of the material in terms of occupation of T-sites by Al and the occupation ratio to Oh-sites : also the effect of different oxygen frameworks (fcc, hcp) on such ratio.

The idea our of simulation is simple. We want to see what kind of Al distribution on Oh and T sites has the lowest total energy, which should tell us something about the structure of g-Al₂O₃. We also want to how the underlying fcc or hcp nature of the oxygen framework affects the ground state distribution of cations. For these purposes, it is sufficient to model the Al₂O₃ systems with interacting Al ions moving among all possible Oh and T interstitial sites of a given (fcc or hcp) oxygen framework. This naturally lead us to the choice of the Lattice Gas type simulation in which the Al ions are treated as gas particles interacting with each other according to J(r_m), and hopping among the discretised lattice points which represents the interstitial sites of the fcc or hcp structures, with an additional chemical potential m on the Oh sites. We also assume that the hopping can only happen toward the nearest neighbouring sites. It is important to note that the potential energy of a given site can be evaluate by using J(r_m) and m from (4.1), so we know which are the lower energy sites to move Al ions to during the lattice gas simulation.

There is a less trivial technical aspect that worth mentioning. It is not directly obvious how to construct the required "lattice sites" (not the lattice in crystallographers' sense) for our lattice gas simulation, in a simple and computationally addressable way, so that they preserve the correct connectivity of Oh and T interstitial sites. For example, in an fcc oxygen framework an Oh-site has 8 nearest neighbour sites, and a T-site has 4. If we represent all possible hops as lines between "lattice points", then we will see regular distribution of 8-arm vertices and 4-arm vertices. Their positions can not be described in terms of any common cubic or hexagonal structures. We have solved this problem by embedding the topology of the Oh and T sites into a denser simple cubic grid, which we found possible for both fcc and hcp cases. We could then express the connectivity between neighbouring interstitial sites in terms of lattice vectors, these vectors then defining all possible hopping directions from a site to its neighbours.

We have performed simulations on both fcc and hcp frameworks representing 864 oxygen ions. In each simulation, 576 Al "particles" are set to be hopping among corresponding lattice sites (864 Oh and 1728 T sites) in a box with periodic boundary condition. The simulation is performed in the way that Al "particles" will only hop to lowest energy neighbouring sites or no hop, therefore the total energy of the system will be reduced with such procedure. Random noise is used occasionally to disturb the system to present it from stuck in some meta-stable state. The noise is not introduced through a temperature variable, though proper simulated annealing with a Boltzman factor can be carried out easily if one needs a more effective search of low energy states. The simulation continues until essentially all movement of Al stops, and then the final positions of these ions are analysed. Various initial conditions, indicated in Table 4.2, were used to ensure a better exploration of structures with minimum total energy.

The following table shows the results of searching in the above way for a low total energy Al population. In the first column "Initialisation" we specify the initialisation condition for the simulation, in which "optimal" means that a well separated initial Al configuration as ordered as possible has been used , "condensed" means all Al ions were packed in a small region in the simulation box at the beginning, and "random" means we randomly placed Al ions in all possible sites before starting. The words "Oh", "T" or "both" appearing as prefixes in this column indicate whether the Al ions initially occupied Oh sites or T sites, or both. For example, "Oh optimal" means all Al ions started from well ordered Oh positions, well separated. The second column "n[Oh]/n[T]" contains the number of Al ions in Oh and T sites respectively as the result of the simulation. The last column "n[Oh]/n[Oh+T]" gives the ratio of Oh sited Al as a fraction of all Al ions. The corresponding value from Solid State NMR measurements, which were carries out after our simulation, as will be mentioned in more detail at the end of this section, are also listed.

[Table 5.1]

Results of simulations for Al in fcc and hcp oxygen structures with various initial conditions.

For the case of fcc oxygen framework :

fcc

ratio percentage

Initialisation n[Oh]/n[T] n[Oh]/n[Oh+T]

Oh optimal 441/135 76%

Oh optimal 441/135 76%

T optimal 408/168 70%

T optimal 415/161 72%

T condense 428/148 75%

T condense 430/144 75%

Oh random 414/162 72%

Oh random 411/165 71%

T random 411/165 71%

T random 417/159 72%

both random 411/165 71%

both random 432/144 75%

both random 419/157 73%

Predicted ratio 73.0%

Solid state NMR Result 70.66% +/- 2.28%

For the case of hcp oxygen framework :

hcp

ratio percentage

Initialisation n[Oh]/n[T] n[Oh]/n[Oh+T]

Oh optimal 576/0 100%

Oh optimal 576/0 100%

Td optimal 576/0 100%

Td optimal 576/0 100%

both condense 568/8 99%

both condense 568/8 99%

Oh random 565/11 98%

Oh random 571/5 99%

Oh random 576/0 100%

Oh random 576/0 100%

Td random 521/55 90%

Td random 576/0 100%

Td random 539/37 94%

Td random 539/37 94%

both random 555/21 96%

both random 513/63 89%

both random 563/13 98%

both random 553/23 96%

both random 556/20 97%

Predicted ratio 97.3%

Solid state NMR result 100% +/- 0.00%

From the above results, we are pleased to find that :

(1) The simulations are stable with respect to all those very different initial conditions. The results predicted an unambiguous n[Oh]/n[Oh+T] ratio of Al ions in g-Al₂O₃, and in particular that the partial occupation of T sites is a energetically stable, not just a kinetic artefact that may come from the various parent materials during the preparation.

(2) The predicted percentage of n[Oh]/n[Oh+T] for g-Al₂O₃ agrees well with experiment, and the simulations also gives the correct ratio (all Oh Al) for a-Al₂O₃. It is clear from our results that the difference between the fcc and hcp oxygen frameworks is responsible for whether the T-site are occupied by some Al ions.

We want to emphasise that the simulations were carries out first so that the percentage of n[Oh] in g-Al₂O₃ was a prediction. Subsequently this ratio was measured at our suggestion with solid state NMR by colleagues Mr. Chi-Feng Cheng and Dr. Jacek Klinowski in the Chemistry Department, Cambridge, with the results shown in Table 5.1. In spite of the problems of obtaining a good fit for the parameters in (4.1) as discussed in connection with Table 4.1, we are gratified that the statistical accuracy of the results from our simulation is already sufficient to resolve the difference between the a and g phases. We therefore claim that we have successfully (a) predicted (and we mean 'predicted', before the experimental determination) the Oh occupation ratio in g-Al₂O₃ and (b) demonstrated the effect of oxygen framework topology on the Al site distribution, by using our very simple model.

VII.6 Discussion : Geometrical Interpretation of Results

The purpose of this section is to explore how far the structural properties of g-Al₂O₃ can be accounted for in terms of the geometrical fcc packing of oxygen atoms in g-Al₂O₃. In particular, we ask whether there are some inherent features of the hcp and fcc oxygen lattices that account for the strong ordering on Oh sites only in one case (a) and occupation of both Oh and T sites in the other (g). In the latter case, can the presence of occupied T sites destroys the long range order ? We shall see that we can indeed interpret the results of the simulations, and experimentally observed reality, along such structural lines.

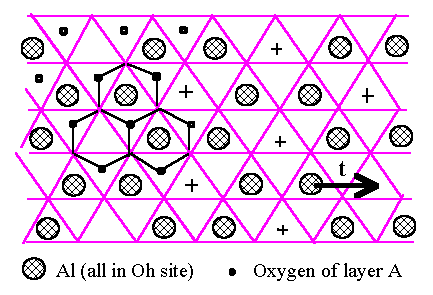
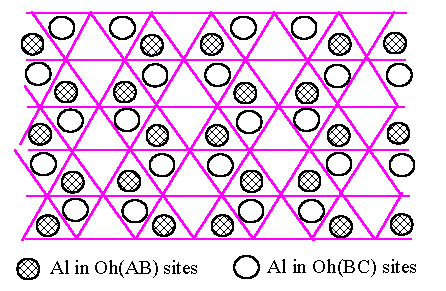
We shall consider the oxygen structure built up of close-packed layers, stacked ABCABC for the fcc oxygen structure and ABABAB for the hcp one, in the usual notation. The Al atoms lie on the Oh and T sites between pairs of oxygen layers (Fig.6.1). We know from the simulations of Section 4 that the Oh sites have lower energy and we therefore start by considering the Al atoms on Oh sites only. We assume that each Al layer to have the same density of Al because it is energetically favourable. The arrangement of Al atoms, occupying two-thirds of the Oh sites because of the Al₂O₃ composition, is unique and rather obvious (Fig.6.1). It is best reviewed by noting that the empty Oh sites are spread out as uniformly as possible in a triangular mesh (shown as + in Fig.6.1). We will refer to Oh and T sites between A and B oxygen layers as Oh_(AB) and T_(AB).

[Fig.6.1]

Arrangement of Al atoms (large shaded circles) on Oh sites between a pair of oxygen closed-packed

layers. The oxygens of the upper layer are at the vertices of the triangular lattice and those of lower

layer at the small dots (only shown on the left). The hexagons on the let are the projection of three

octahedra, tow filled with Al and on empty. The empty Oh sites are marked on the right side of the

figure by +. Two types of (empty) T sites lie directly above the lower (A) layer and directly below

those of upper (B) layer.

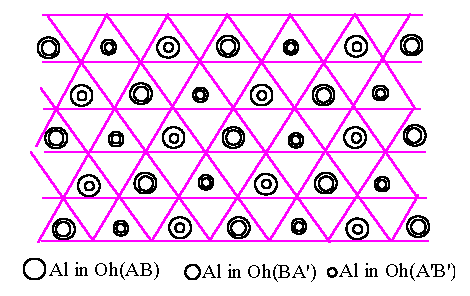
We now turn to the three-dimensional stacking of oxygen and Al layers, starting with the hcp oxygen structure. The Oh(BA') sites between BA' pair of oxygen layers are directly above the Oh_(AB) sites of previous (AB) pair of oxygen layers in the ABA'B'A''B'' stacking of the hcp oxygen structure, where the primes simply distinguish successive layers of the same type. Let us assume that the Al atoms between the A and B oxygen layers conform to the arrangement of Fig.6.1. The Oh_(BA') sites of the next BA' pair of oxygen layers lie directly above the Oh_(AB) sites and we can arrange that the Al atoms on Oh_(BA') sites follow the same pattern but displaced by the vector t shown in Fig.6.1. In this way all the sites above the empty Oh_(AB) sites (shown as + in Fig.6.1) are filled which must be energetically most favourable because this minimises the number of face-sharing Al octahedra between two layers. That accounts for the half of the Al atoms between the BA' oxygen layers, and the other half then spread themselves out to make the unique pattern of Fig.6.1 again but displaced by t as already mentioned. We conclude that for ABABAB oxygen packing, a very good, low energy structure results from placing all Al in Oh sites, with those in one Al layer displaced by t with respect to the adjacent one : this is not true for the fcc ABCABC stacking as we shall see below. We now turn to adding the third Al layer, assuming (without lost of generality) that the second Al layer is displaced by +t with respect to the first. The third layer can be displaced by +t with respect to the second, yielding Fig.6.2.(a), or -t yielding Fig.6.2.(b). These are clearly not equivalent. The former has lower energy because the Al atoms are more uniformly spread out, with no second neighbour face-sharing octahedra. In Fig.6.2.(a), half of the Al atoms are in continuous columns as shown by the triple circles. We conclude that we would expect the lowest energy structure based on hcp oxygen packing to have Al layers displaced successively by +t, +t, +t, +t, ..., and this is indeed the a-Al₂O₃ structure. We note that each Al has only one face-sharing neighbour across the oxygen layers, i.e. one-half such pairing per atom. The dominant energy cost of the stacking is therefore (1/2)J(r_face) per atom if we take into account the decrease of J(r_ij) with distance, which is very low compared with the fcc result as we shall see below.

[Fig.6.2]

Al atoms (large, medium and small circles) in Oh sites between successive pairs AB, BA' and A'B'

of oxygen layers in an fcc oxygen structure, where A', B' are next A-type and B-type layers.

[Fig.6.2.(a)]

As in a-Al₂O₃

[Fig.6.2.(b)]

In an unobserved structure

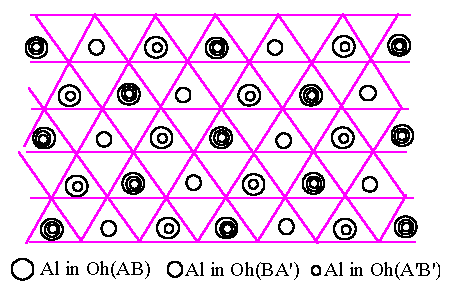
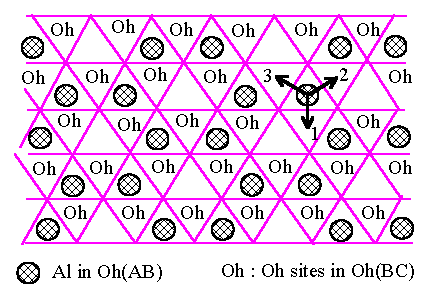
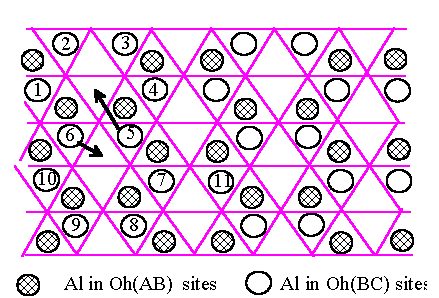
We can now see what happens when we try to apply the same types of argument to g-Al₂O₃ with ABCABC oxygen stacking. We start again with the Al atoms as in Fig.6.1 in the first Oh_(AB) layer. The next oxygen layer is now C-type so that the Oh_(BC) sites are now differently placed from the Oh_(BA') sites before, as shown in Fig.6.3 : i.e. adjacent layers of Oh sites have a different relation in the fcc oxygen lattice from that in the hcp case. All the Oh_(BC) sites are equivalent in Fig.6.3 as regards their positioning with respect to the Al atoms in Oh_(AB), so that the lowest energy structure will again be that of the hexagonal rings in Fig.6.1, now displaced by one of the three equivalent vectors pointing to site 1, 2 and 3 indicated in Fig.6.3. Fig.6.4 shows one such arrangement, and we can assess its energy in a similar way to before. Each Al atom in Oh_(BC) now has two edge-sharing contacts with Al in Oh_(AB) octahedra and we can write the dominant term in the stacking energy as 2J(r_edge) per atom. We have r_edge = 1 d_O-O (d_O-O is the ideal oxygen close-pack distance) and r_face = d_O-O so that r_edge/r_face = 1.22. Thus we expect 2J(r_edge) to be substantially larger then (1/2)J(r_face) and thus Al inter-layer energy in fcc oxygen structure to be substantially higher then in the hcp case, i.e., we expect that the a-Al₂O₃ structure will have lower energy than g-Al₂O₃ based on an fcc oxygen structure.

[Fig.6.3]

Al atoms (shaded circles) in Oh sites between one AB pair of close-packed oxygen and all Oh

sites (marked "Oh") between the next BC pair of oxygen layers in an fcc oxygen structure.

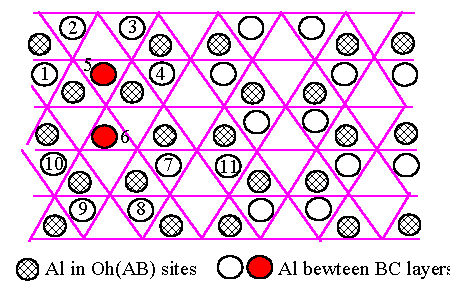
[Fig.6.4]

Al atoms (shaded circles) in Oh sites between an AB pair of oxygen layers, and one of

three equivalent arrangements of Al atoms (empty circles) in OH sites between the next

BC pair of oxygen layers in an ABCABC fcc oxygen structure.

We can now consider whether the energy in the fcc oxygen framework can be lowered further by moving some Al atoms from Oh to T sites. The optimum configuration of two adjacent Al layers based on Oh sites along has already been derived in Fig.6.4 and is reproduced in Fig.6.5.(a). A typical Al atom such as number 6 is edge sharing with 5 other Al octahedra, namely those numbered 1, 5 and 10 plus two Al in Oh_(AB) shown as shaded circles. If it is displaced by vector shown in Fig.6.5.(a) to a neighbouring T site several of these bonds are broken, and if Al atom 5 move simultaneously out of the way by the vector also shown in Fig.6.5.(a), we obtain the structure shown in Fig.6.5.(b). This has three less edge-sharing Al neighbours but there is now one T-site Al which cost an energy |m| in the sense of equation (1.1) and (4.1). The tetrahedron occupied by atom 6 only shares corners with surrounding Al octahedra, so that its electrostatic energy is not high. We conclude that the movement of some Al atoms from Oh to T sites such as in Fig.6.5.(a),(b) is expected to lower the total energy, as shown by the simulation in Section 5.

[Fig.6.5]

[(a)]

Two Al atoms, numbered 5 and 6, taken from Oh sites in the configuration

of Fig.6.4 on an fcc oxygen structure, and moved to tetrahedral (T) sites.

[(b)]

The final configuration

The final step in our argument is to consider why the occupation of T sites may destroy the long range order in the structure based on the fcc oxygen lattice. There are of course many pairs of Al atoms such as 2,3 and 8,9 and 7,11 which could make a similar transformation to Fig.6.5.(a),(b) resulting in a T site. However once atoms 5 and 6 have transformed, it is no longer energetically favourable for the 7,11 pair to do so too because the movement of atom 5 has already removed an edge-sharing neighbour from atom 7. Similarly, the equivalent transformation for the pair 8,9 in Fig.6.5.(b) would place atom 8 too close to atom 6, making this more energetically unfavourable. Such arguments apply altogether to four pairs around the 5,6 pair. Thus the total number of occupied T sites is not expected to be very high, with an exclusion zone without other Al T-atoms around each one. The process of generating Al-T-atoms can therefore nucleate in different places in mutually incompatible ways, thus destroying the long range order. An equivalent way of expressing the same thing is to say that a modest proportion of Al on T-sites generates a substantial configurational entropy, which can destroy long range order at a relatively low temperature.

In conclusion, we have seen that we can make plausible arguments to explain what is observed in the simulations and experimentally on a-Al₂O₃ and g-Al₂O₃, namely (a) that the Al ordering in a-Al₂O₃ is very good leading to its being th lowest energy structure, in comparison with other Al ordering patterns on Oh sites in an hcp oxygen lattice, (b) a similar good Al ordering pattern cannot be achieved on the Oh sites only for an fcc lattice, leading to some Al on T-sites in a-Al₂O₃, and (c) the occupation of some T sites in g-Al₂O₃ tends to destroy the long range order.

VII.7 Plans for Possible Further Work

The research on g-Al₂O₃ was stopped at a convenient point after completing what is really an extensive preliminary survey. The gratifying surprise is that it has already yielded an understanding of the main feature of g-Al₂O₃, both semi-qualitatively in terms of the simulations of Section 5 and the geometrical insight in Section 6. This fully justifies the basic methodology of the using of the model Hamiltonian as an intermediate step.

However some modest tidying up is clearly indicated. the simulation of a and g structures need repeating as proper simulated anneals at temperature T with the Metropolis algorithm. Then the results need more detailed analysis of the short and long range order. A further avenue of research is to improve the fit of the model Hamiltonain to the 9 energies calculated ab initio, by doing a least square fit or perhaps by expressing the J(r) as a Coulomb term plus local strain corrections for nearest neighbour face, edge or corner sharing of occupied octahrdra and tetrahedra.

Much more extensive computing would be required either to extend significantly the data base of ab initio configurations, or what is really more important, to relax the oxygen positions and thus take local stain effect into account.

However one of the original hope has been to address surface properties, including perhaps the energies of different crystal surface orientations. These may throw light on the reason why g-Al₂O₃ is almost only found as a very fine microcrystalline powder. In view of what has been said, an extensive ab initio study of surface energy of different surface is (regarding the power of computers today) out of the question. However we can speculate and propose one or two likely structures based on our model Hamiltonian and perhaps do ab initio calculations of total energy relaxing oxygen and Al positions but not site occupancies. A 3-step approach similar to the one introduced in this chapter, with extra fit-able terms in model Hamiltonian that account for the surface configuration, can also be used to study the structure and energetics of the g-Al₂O₃ surfaces.

One way to rationalise the fact that g-Al₂O₃ almost only exist in fine powder is to say that nucleation energy is very low because the surface energy is very low. The point is that with g-Al₂O₃ being disordered, the Al configuration at a surface can itself to minimise the surface energy which might result in a very low energy value, at least for some specific surface orientation(s). This could be explained within the existing model Hamiltonian and perhaps followed by one or two ab initio calculations mentioned. However one note of caution should be mentioned. The model Hamiltonian does not contain the long range Coulomb interaction between Al ions. This may not be very important for the bulk structure with Al more or less uniformly spread out, but could be an important aspect of surface energies. This could probably be modelled by a shell model simulation as an intermidiancy between our full ab initio technique and the rather crude model Hamiltonian.

Acknowledgments

I would like to thank :

Mr. C.-F. Cheng's close collaboration with us on the experimental investigation of the material.

Dr. X. Yuang for kindly provide us part of the a and g-Al₂O₃ sample.

Dr. Macrod bring g-Al₂O₃ to our interest and collaborated with us at the early stage of the project.

Dr. S. Bhattacharjee for the discussion on a-Al₂O₃ at the early stage of the work.

Prof. McConnell for his inspiring suggestion on the projects of alumina in general.

Prof. Andaus Carson for the discussion on cluster-cluster interaction.

Prof. C. Cheng for useful discussion of the error tolerance total energy in a variety of systems.

References

[C.1]

Y.T. Chu, J.B. Bates, C.W. White , and G.C. Farlow, J. Appl. Phys. 64 (7) 3727-3730 (1988)

[C.2]

T.C. Chou and T.G. Nieh, J. Am. Ceram. Soc., 74 [9] 2270-2279 (1991)

[C.3]

C.R. Catlow and W.C. Mackrodt (eds), Computer Simulation of Solid, Lecture Note in Physics, 166 (1982)

[D.1]

B.G. Dick and A.W. Overhauser, Phys. Rev. 112, 90 (1958)

[G.1]

N.N. Greenwood and A. Earnshaw, Chemistry of The Elements, Ch.7, Pergamon Press (1990)

[H.1]

V. Heine, private communications by W.C. Mackrodt, D. Bird, P. Madden and others

[I.1]

H. Iizuka, K. Yokoo and S. Ono, Appl. Phys. Lett. 61 2975 (1992)

[O.1]

H. O'Neill, A talk given in "ESF Progam on Kinetics of Minerals and Ceramics" (4th Feb 1994)

[P.1]

M.C. Payne, M.P. Teter, D.C. Allan, T.A. Arias and J.D. Joannopoulos, Rev. Mod. Phys. 64 No.4, 1045 (1992)

[R.1]

A. Reller and D.L. Cocke, Catalysis Letters 2 (1989) 91-96

[S.1]

J. Schafer and C. J. Adkins, J. Phys.: Condens. Matter 3 2907-2915 (1991)

[S.2]

R. Serimaa, Acta Polytechnica, Applied Physics Series No. 169 (1990)

[S.3]

P.S. Sklad, J.C. McCallum, C.J. McHargue and C.W. White, Nuclear Instruments and Method in Physics Research B46 102-106 (1990)

[W.1]

S.J. Wilson and J.D.C. Mc Connell, J. Solid State Chem, 34, 315-322 (1980)