I

An Introduction to Pseudopotentials

and

Total Energy Calculations

I.1. Overview of Chapters

Almost the whole thesis (Chapter I to Chapter VI) is devoted to improving the generation of pseudopotentials for case in electronic structure calculations of solid (or systems that can be treated with supercell geometry). On the one hand I have improved the techniques of generating pseudopotentials. On the other hand these new ideas (which has been very largely my own) have also helped us to understand better the process of generating a good pseudopotential and thus to demystify considerably what has been described as its "Black Magic". These techniques and ideas have been applied to generate around 50 pseudopotentials for specific applications, almost all being carried out by other people.

The remainder of the present chapter (Chapter I) will be devoted to background information, namely some relevant points from the history and theory of pseudopotentials and from the technique of total energy calculations.

In Chapter II we will report some important insights into the popular Optimised Pseudopotential [Ref.R.1,L.1] methods. We will present a new way (with examples) to use the optimisation q-vector cut-off Q_c, as well as other factors such as the number of constraints imposed and the number of special function terms used. The important message of this chapter is that the Q_c can be varied to control the shape (and therefore plane wave energy cut-off) of the pseudopotential, and also to affect the logarithmic derivative of the wave function. Understanding the role of Q_c in the optimisation procedure enable us to generate better pseudopotentials in a more systematic way based on established schemes for Optimised Pseudopotentials.

In Chapter III we will propose an extension of the way we use our new Q_c-tuning Optimisation scheme. Optimisation has long been used solely to treat the harder components of a non-local pseudopotential (i.e. "hard" as the opposite of "soft", meaning having significant high Fourier components : we shall always use "hard" in this sense) , and we will show the benefit of tuning Q_c for other components. The idea is to make some of the components very similar so that they can be represented to sufficient accuracy by the same local potential, which will reduce the computational effort in subsequent total energy calculations. We called this technique Projector Reduction. Some atomic and solid state tests will be provided to show that the technique is reliable. The success of Projector Reduction emphasises the advantage of having a flexible control of the shape of a pseudopotential.

Chapter IV is to ask the question : "How local can one make a pseudopotential ?". There has been an observation that some elements can be described by a local potential but others cannot. The success of the technique proposed in Chapter III motivates us to investigate this issue. We generate non-local pseudopotentials with the method introduced in Chapter II and III, and try to make these pseudopotentials as local as possible. In other words, we will present a new approach to construct local or partly-local potentials from a non-local method, which allow us to investigate the degree of essential non-locality of a pseudopotential.

A large proportion of our experience on pseudopotentials has come from collaborations and supplying a service. Chapter V is a short one which comprises a brief description of the pseudopotentials generated both for general usage and for some special applications. Detailed generating parameters for these pseudopotentials will also be given.

In Chapter VI we will mention some ideas for further research in the field. I have noticed several interesting aspect of pseudopotential generation and usage which might merit attention. We will present some very preliminary results for them. These relate to three aspects of pseudopotentials, namely pseudo core overlap, even softer potentials, and the some special cases among the I-A and II-A group elements of the periodic table.

Finally, Chapter VII is an application of the ab initio electronic structure total energy method to study the origin of the disorder in a complex solid g-Al₂O₃. In this study we have used a three-step approach which combines first principle calculations, a model Hamiltonian and then simulation. The methodology allows us to study the origin of disorder in this weakly ordered material with a modest computational cost. It is a preliminary survey for further studies in Al₂O₃ systems that we have planned to do.

Although the electronic structure total energy calculation is presented in this thesis as an independent chapter in the context of the study of the g-Al₂O₃ (Chapter VII), all the solid state tests for the pseudopotentials in the thesis were done by using the same ab initio total energy method. In some cases these were done on semiconductors, in other cases insulators or metals, and even isolated molecules. These tests are not described separately, just mentioned briefly where relevant.

I.2. Background Information: Essential Theory of Pseudopotential

In the following sub-sections we will review some essential points from the theory of pseudopotential that are relevant to the following chapters of this thesis. The intention is not to develop a full comprehensive discussion but to provide the background information that will be needed in this thesis.

I.2.0 What Is A Pseudopotential and How Is It Used ?

A pseudopotential is an effective potential for valence electrons in an atom, molecule or solid. It represents the effects of both the core-electrons and the nuclear Coulomb potential acting on the valence electrons. In other words, a pseudopotential is used to reproduce the correct valence charge density outside the range of the pseudopotential (i.e., outside the pseudising core region) without treating the core electrons and the atomic nucleus explicitly. Inside the pseudising core the distribution of the valence charge density is not correct, but this causes little disadvantage on most solid state problems because the physical properties and chemical bonding are dominated by the electronic structure of valence electrons between the ions. This means that the modification of the electronic structure inside the pseudising radius region has minimal effect on the calculated properties of solids and molecules. The decoupling of valence and core electrons is a very good approximation as can be seen throughout chemistry, which is based mainly on the effect of the valence electrons.

The advantage of using pseudopotentials in electronic structure studies is most obvious when the wave functions are expressed in terms of a plane waves basis set. This is because the pseudopotential is much weaker than the true potential so that the Bloch wave functions need only a fairly modest number of plane waves in the expansion.

From the view point of the APW (Augmented Plane Wave) method [Ref.H.3] we know that the energy dependent logarithmic derivative R'_l(r,E)/R_l(r,E), in which the R_l(r,E) is the solution of the radial Schrödinger equation at energy E, plays the central role in representing the effect of the potential energy on the valence electrons in the APW formalism. Also from the wave scattering theory we know that the phase shift, which is closely related to the logarithmic derivative, of the scattered wave characterises the interaction between the wave function and the scattering potential. It is therefore not difficult to understand that the accuracy of a pseudopotential is determined by how closely it reproduces this logarithmic derivative. As an approximation, this logarithmic derivative is only correct in a certain range of the energy, namely that of occupied reference orbitals. This is generally true for all types of pseudopotential, and we will use the example of the OPW (Orthogonalised Plane Wave) type pseudopotential later to demonstrate such energy dependence.

The logarithmic derivative of the wavefunctions is particularly important for a special family of pseudopotentials, namely Norm-conserving Pseudopotentials, as we will discuss later in this chapter. The condition of giving the correct phase shift also guarantees the right electrostatic contribution from pseudopotentials, so that the phase shift (which is directly relate to the logarithmic derivative) is also seen from this point if view as a central criterion for pseudopotentials.

I.2.1. The OPW (Orthogonalised Plane Wave) View Point

The most significant effect of core electrons on the valence electrons is the orthogonality between their wavefunctions. Some basic ideas of pseudopotentials can be easily demonstrated by following the OPW type pseudopotential approach which we will discuss here.

Let Y be a state vector and e be its energy eigenvalue. Then the Schrödinger equation is

. (2.1.1)

We may write Y in terms of a smooth function F and an oscillatory part which is a linear combination of core eigen states F_c, with coefficients b_c

(2.1.2a)

where the can be determined by the orthogonality condition

(2.1.2b)

giving . (2.1.2c)

If we take this expression for Y back into equation (2.1.1), we have

(2.1.3)

which can be rewritten

(2.1.4a)

with (2.1.4b)

where T is the kinetic energy. The message we receive from this OPW type approach is that the new pseudo Schrödinger equation (2.1.4) gives the same energy eigenvalue as the original one. The true potential V in original Hamiltonian H has been replaced by an "energy dependent" effective "pseudopotential" V_ps (2.1.4b) where major difference from true potential lies in the core electron region. At the same time the true wavefunction Y is replaced by a pseudo-wavefunction Y_ps which has no effects from core-orthogonalisation and so should be much smoother than the original wavefunction.

I.2.2 Ab initio Pseudopotentials from Pseudising and Inverting Wave Functions

Almost all modern pseudopotentials use ab initio atomic wavefunctions to obtain pseudopotentials. The valence wavefunction for each angular momentum l obtained from solving radial Schrödinger equation is modified within a pre-chosen pseudising radius r_c (called the pseudising or pseudo-core radius, or often just radius for short) to a create nodeless pseudo-wavefunction. The pseudo wavefunction is then introduced back into the radial Schrödinger equation to find the l-dependent pseudopotentials that will reproduce the energy eigenvalues when acting on the pseudo wave function. The formalism is briefly sketched as follows.

When we perform an atomic calculation, we are solving self-consistently the following set of equations with different l for the radial wave functions defined by Y_lm(r) = r^-1F_l(r)Y_lm(q,f) of the occupied orbitals with eigenvalues E_l :

. (2.2.1)

Keeping the same E_l in the equation, we replace the real (screened) potential by a (screened) pseudopotential

. (2.2.2)

How F_l,ps is generated from F_l varies from one method of generating pseudopotentials to another. It is not unique and is the crux of each scheme. It will be discussed for our method in detail later.

The point common to all the methods is that F_l has been modified such that F_l,ps is nodeless, but is equal to F_l outside r_c. Having first obtained a suitable F_l,ps we can then invert (2.2.2) to give the value of pseudopotential V_l,ps(r) in terms of the inverse and the second derivative of the one-particle pseudo-wavefunction :

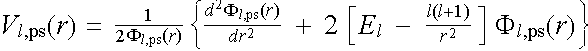(2.2.3)

(2.2.4)

This is the l dependent (screened) pseudopotential that is seen by the l-state pseudo-wavefunction . Through this procedure, for each l we have one V_l,ps(r). These potentials act on the respective l state, and include the screening of the atomic core by the charge density of all l states in the valence shell.

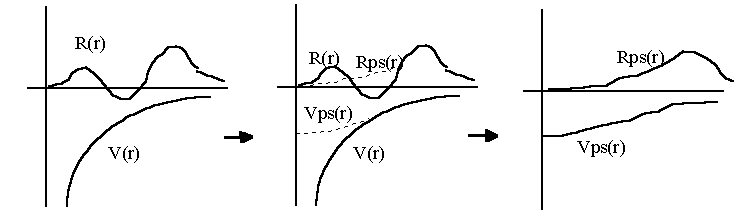
In short, the two stages of pseudising a wavefunction and inverting the Schrödinger equation from the pseudised wavefunction can be visualised with the following figures :

I.2.4 Unscreening Pseudopotentials

The way we want to use a pseudopotential in solid state calculations is to find the ground state of the valence electrons in a self-consistent way, and therefore the information of valence electron charge density has to come from the solid state calculation. We want the pseudopotential not to carry the valence electron screening of the free atom so that we can add later the solid state one. This is the reason why we need to unscreen the atomic pseudopotential for each l components. The (potential) energy contribution due to the valence charge density must be subtracted away to give an ionic pseudopotential :

_{free atom} (2.4.1)

where

, and (2.4.2)

. (2.4.3)

Note that V_XC [r(r)] = V_XC [r_valence(r) + r_core(r)] is not equal to V_XC [r_core(r) ] +V_XC [r_valence(r)] because of the non-linearity of the function r(r). To subtract the valence charge density's contribution to exchange-correlation energy, we can follow one of two options. The first is to freeze the core-valence exchange-correlation interaction so that the ionic pseudopotential carries along with itself this energy evaluated from the atomic state and uses it in all the solid state environment. Alternatively we can subtract the term V_XC [r(r)] entirely, just pass the core charge density r_core(r) to the solid state calculation and evaluate V_XC [r(r)] for the solid as V_XC [r_core(r) + r_band(r)] later on.

As for the term V_Hatree[r(r)], since it is a linear function of r(r), so the subtraction of the energy contribution from the valence charge density is exact.

I.2.5 Norm-conserving Pseudopotentials

Before the work of Hamann, Schluter and Chang (Ref.H.2, to be refer as HSC), pseudopotentials suffered from two problems. Firstly there was no guarantee that the amount of charge

inside the core-radius r_c is conserved in going to the pseudo wave function. In order to obtain sensible electrostatic energy, for example in calculating the energy difference between two structures, we need to have equivalent electron densities, which is achieved nearly enough if

. (2.5.1)

The second problem concerned the logarithmic derivative. This was fixed to be the same for the Y_l and Y_l,ps at some energy eigenvalue E_l , but for a good pseudopotential we would like it to be the same (or very nearly so) over the energy range of the occupied valence orbitals of the solid. This is to say that we would like also

. (2.5.2)

HSC pointed out that if we make the pseudopotential satisfy the Norm-conserving condition (2.5.1), then (2.5.2) is also satisfied automatically. The reason is that the two quantities are linked by the identity

. (2.5.3)

In the original paper of HSC only a hint is given to the proof. Here we will try to follow the hint and prove this condition.

Let . Then the l-state radial Schrödinger equation at different energies and becomes

,

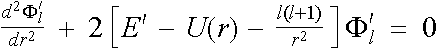. (2.5.4)

we multiply the first by F_l' , the second by F_l , subtract and eliminate common terms. We have

,

Which integrated from r = 0 up to r = R becomes

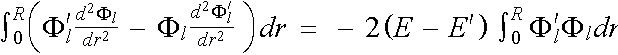. (2.5.5)

The left hand side of the equation can be integrated out by parts to give

LHS. of (2.5.5) = 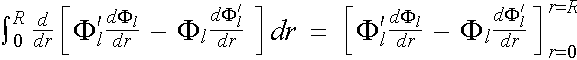, (2.5.6)

in which the terms in the square brackets [ ] can be further simplified to

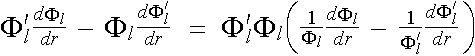(2.5.7)

. (2.5.8)

Introducing the result back into equation (2.5.5), we have

(2.5.5) 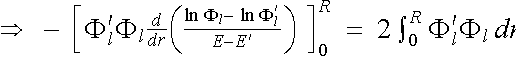. (2.5.9)

In the limit E - E' 0 we obtain the differential form

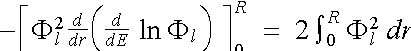. (2.5.10)

Note that the Norm-Conservation Condition only guarantees the correctness of the logarithmic derivative to first order in the energy variation.

Since , we have

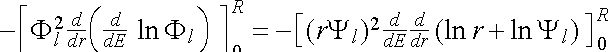
. (2.5.11)

The factor of r² ensures that the limit r = 0 contributes zero in the last term in (2.5.11). This leaves only the upper limit at r = R, which is then substituted back into (2.5.10).

We have therefore proved the Norm-Conserving Condition

(2.5.12), (2.5.3)

I.2.6 The Kleinman-Bylander Form of A Pseudopotential

We now make two transformations on the pseudopotential. The first is rather trivial. Let V_l be the l-component of the (unscreened) ionic pseudopotential in the sense of Section I.2.4. we can choose some arbitrary local potential V ^L , i.e. the same for all l, to and write

V_l = V ^L + dV_l (2.6.1)

where dV_l = V_l - V ^L . (2.6.2)

The whole ionic pseudopotential can then be conventionally expressed as

V_ion = S_lm |Y_lm> V_l <Y_lm| = V ^L + S_lm |Y_lm> dV_l <Y_lm| , (2.6.3)

where |Y_lm> and <Y_lm| project out the l, m component of the pseudo wave function. The Hartree field and exchange-correlation potential of valence electrons are also local functions with the use of Local Density Approximation for exchange and correlation so that they can be added to V ^L without changing the dV_l . The second transformation is to write the last term of (2.6.3) in the approximate form

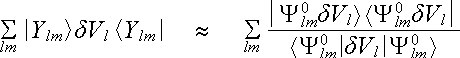, (2.6.4)

in which Y⁰_lm(r) = j^PS_l(r)Y_lm(q,f), with j^PS_l(r) being the pseudo wavefunction used to create V_l(r). We therefore have

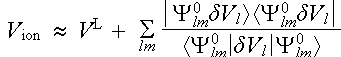, (2.6.5)

which is the Kleinman-Bylander form of the pseudopotential. To see its relation to (2.6.3) we operate with it on Y⁰_lm to the left and right . We see that the two forms in (2.6.4) give identical results in this case because one factor of <Y⁰_lm|dV_l|Y⁰_lm> on the right side. We now make the argument that the l, m angular momentum component of any pseudo wave function in the solid can be expected to be approximately like Y⁰_lm over the region inside r_c. With that assumption the two forms in (2.6.4) become equivalent to a sufficient degree of approximation.

What has been gained by this transformation is an enormous increase in computational efficiency. Suppose we use N plane waves (N ~ 10000) as basic functions. The N x N representation of V_ion requires in principle the calculation of N² numbers using the full non-local form (2.6.3). However the Kleinman-Bylander form (2.6.4) only requires evaluation (for each l, m) the N quantities

<Y⁰_lm|dV_l| Plane-wave n> (2.6.6)

and taking products of them.

I.2.7. BHS table for excited states, and comments

A problem arises in generating pseudopotentails V_l for the higher values of l when there are no filled orbital in the free atom with that l, e.g. V_l=2 for all elements in periodic table up to Ca. The problem is compounded when later transforming to Kleinman-Bylander form. Although there are no occupied orbitals with this l in the free atom, in general any wave function in a solid will contain components of all l when expanded around an atomic site, so that the V_l for such l is needed in the solid state calculation.

In generating the pseudopotential with such an l in the manner of Section I.2.3, we need the corresponding radial atomic orbital F_lm and eigenvalue E_l. Such an unoccupied state in the atom may be totally unbound so that E_l may not exist : but even if it is bound, it is very likely loosely bound so that its E_l is not in the range of the occupied states of the solid. In that case matching the logarithmic derivative at E_l leads to significant errors in the energy range of interest in the solid.

A further problem arises with the use of the (2.6.5). If the atomic F_l is very loosely bound, it will not have the form of the l components of the occupied states of the solid which are much more strongly bound. Hence the argument used to demonstrate the equivalence of the two forms in (2.6.4) is no longer valid, and significant errors are to be expected.

Actually, it is convenient to test the logarithmic derivative of the pseudopotentail and to carry out the Q_c-tuning in its ultimate Kleinman-Bylander form. This avoids, or rather cancels, any error inherent in the transformation.

To overcome these problems, Bachelet, Hamann and Schluter (Ref.B.1, referred as BHS) published a table of atomic excited configurations in which an electron (or more often a fraction of one) is promoted into the orbital with the desired l. In this way more relevant atomic eigenvalue E_l and orbitals Y_l are obtained. But the procedure is rather arbitrary and it may be necessary to check that E_l really lies in the range of occupied orbitals of the solid (taking into account the atomic unscreening and addition of the solid state Hartree potential).

I.3. Total Energy Calculation

Describing the bonding between atoms accurately is essential for computer experiments at the microscopic level. This is why a quantum mechanical treatment of the electronic structure is necessary.

In the study of a condensed matter system, a typical number of 10²³ electrons is involved, which makes it an extremely complicated quantum many-body problem. We therefore can only study solid state physics with a certain degree of approximation. On the other hand, we do not need to know detailed information for each electron in a solid. The Density Functional Theory (DFT) [Ref.D.1,P.4] is a useful representation of quantum mechanics for large number of interacting particles. The theory says that there is a unique correspondence between the ground state total energy and the ground state charge density, i.e. the ground state total energy of a system is a functional of its charge density.

If one treats the ions as classical particles, then the ion-ion interaction is trivial ( and in a supercell geometry can be treated using Ewald summation.). Only the electronic part needs to be treated quantum mechanically. For a given ion arrangement, the total electronic energy in DFT can be expressed in terms of functionals of kinetic energy T_m[r], electron-electron repulsion E_ee[r] and external (potential) energy E_ext[r] (which contains effects such as electron-ion interaction), as the following :

E_e[r] = T_m[r] + E_ee[r] + E_ext[r], (3.1.1)

where r(r) is the electron density. However, the kinetic energy functional T_m[r] for interacting particles is unknown, so that one can not evaluate E_e[r] using (3.1.1), without using an approximate form for T_m[r] such as the Thomas Fermi model which is not very accurate. A practical scheme for evaluating E_e[r] was proposed by Kohn and Sham [Ref.K.2] which expresses the E_e[r] as

E_e[r] = T_s[r] + E_xc[r] + E_H[r] + E_ext[r]. (3.1.2)

in which the T_s[r], E_xc[r] and E_H[r] are kinetic energy, exchange-correlation energy, and classical repulsion of electrons (Hartree energy), respectively. In the Kohn-Sham (KS) scheme [Ref.K.2], the interacting many-body problem (3.1.1) is mapped onto a non-interacting one (3.1.2) within the framework of Density Functional Theory, i.e. the energies are still functionals of the density. These non-interacting particles are described by wave functions called KS orbitals which will still give the same ground state density,

r^KS(r) = S_i |Y^KS_i(r)|² = r(r) . (3.1.3)

The advantage of KS scheme is that the exact form of the kinetic energy functional T_s[r] for the non-interacting particle is known, which is just the expectation value of the kinetic energy of the KS orbitals in the standard quantum mechanics sense.

The non-trivial many-body effect in the Kohn-Sham scheme is included in the exchange-correlation term E_xc[r] in (3.1.2). This is essentially a sophisticated mean field approach, in which the non-locality of the exchange-correlation potential e_xc(r), defined by e_xc(r) = dE_xc[r]/dr(r) , can be rationalised as the result of a dynamical mean field. However, the exact functional form of E_xc[r] is still unknown, so that some approximation has to be made to evaluate e_xc(r). Fortunately, the Local Density Approximation (LDA) works surprisingly well. It approximates e_xc[r] as e_xc(r) which depends only on the charge density locally, and e_xc(r) can be parameterised using the accurate values known for the ground state of the electron gas [Ref.C.1]. The LDA satisfies the sum-rule for the exchange and correlation hole and gives very good structural properties for molecules and solids, but it overestimates the binding (cohesive) energy. The Generalised Gradient Approximation (GGA) includes gradient terms in e_xc , which improves the binding energy, but has been reported to give worse bulk moduli of solids [Ref.J.1].

To solve for the energy in (3.1.2), it is necessary to find the wave functions, charge density and the energies. For this one needs to minimise (3.1.2) to find the ground state. The r in the ground state of the system satisfies the variational condition dE_e[r]/dr(r) = 0 which gives KS equations, a set of one-particle Schrödinger equations with an exchange-correlation potential e_xc(r),

[H^KS-E_i] Y_i = . (3.1.4)

The operator in (3.1.4) itself is the gradient operator of this energy minimisation problem, and operate with it on the trial wave functions yields the gradient vector pointing towards lower energy. When this vector eventually vanishes after iterative computing, (3.1.4) is satisfied and the solution is found. To actually perform such "direct" minimisation procedure, the steepest decent method seems to be a natural choice, but it is not suitable for successive searches for the minimum because it makes "right angle" turns everytime at each new step. The more efficient conjugate gradient minimisation [Ref.P.1, P.2, P.3] uses the information from the previous step to search for the minimum. In addition, since the gradient of the wavefunction has an explicit dependence on the energy eigenvalue of the wave function [Ref.P.1, P.3], it is important to precondition these gradient vectors by re-scaling their (energy dependent) weight to achieve an even better overall smooth convergence.

From the above description we know that carrying out the operation in (3.1.4) on a wave function is one of the main computing tasks (others including making the KS orbitals orthogonal). In the basis-set formalism, the kinetic energy operator of the Hamiltonian is diagonal in k-space but the potential energy one is only diagonal in r-space. A significant efficiency can be achieved by using Fast Fourier Transform (FFT) to convert wave functions back and forth between k and r spaces, and by performing these two types of operation in their diagonal from.

After the electronic ground state is found, for a given ionic configuration, the force on each atom can be evaluated directly from wave function by the Hellmann-Feynman theorem [Ref.D.1,P.4], which means that there is no need to perform the derivative of the total energy with respect to ion positions numerically. The force on each atom can then be used to relax the ionic position in order to search for the overall minimum energy of the entire system and find the equilibrium atomic geometry. In a supercell calculation, the stress on the cell can also be calculated from first principles [Ref.N.1].

Pseudopotentials are involved in all three terms e_xc , e_H and e_ext in (3.1.4) in several ways. These come from different aspects of the pseudopotential method and its approximations, namely the Non-linear Core-correction (Chapter I, Section I.2.4 and Chapter VI, Section VI.1), Core Over-lap (Chapter VI, Section VI.1) and Softness (Chapter II and Chapter VI, Section VI.2). We will discuss these points in more detail in the relevant Chapters. The reason that pseudopotentials play such a significant effect role in (3.1.2) and (3.1.4) is basically because pseudopotentials represent the combined effect of both core electrons and the nucleus on the valence electrons. It is therefore important to develop the best strategies for using pseudopotentials in total energy calculations. For large scale electronic structure calculations it is most favourable to use a low energy cut-off of the plane wave basis set, but many plane waves are needed to describe rather tightly bound orbitals such as those of 2p and 3d valence states. How to make a pseudopotential softer therefore becomes important, which will be discussed in Chapter II. As we will see in the Chapter III and IV, non-locality in pseudopotentials is important for accurate calculation but it is expensive, and sometimes problematic. In this thesis we will provide a few new techniques to address these issues in relevant chapters.

Reference of This Chapter

[B.1]

G.B. Bachelet, D.R. Hamann, and M. Schluter, Phys. Rev. B 26, 4199 (1982)

[C.1]

D. M. Ceperley and B. J. Alder, Phys. Rev. Lett. 45, 566 (1980)

[D.1]

R. M. Dreizler and E. K. Gross, Density Functional Theory - An Approach to the Quantum Many-Body Problem, Springer-Verlag (1990)

[H.1]

V. Heine, Pseudopotential Concept, Solid State Physics Vol.24 (1970)

[H.2]

D.R. Hamann, M. Schluter and C. Chiang, Phys. Rev. Lett 43, 1494 (1979)

[J.1]

Y-M. Juan and E. Kaxiras, Phys. Rev. B 48, 14944 (1993)

[K.1]

L. Kleinman and D.M. Bylander, Phys Rev. Lett. 48, 1425 (1982)

[K.2]

W. Kohn and L. S. Sham, Phys. Rev. 140, A1133 (1965)

[L.1]

J-S. Lin, A. Qteish, M.C. Payne and V. Heine, Phys. Rev B 47, 4174 (1993)

[P.1]

M. C. Payne, M. P. Teter, D. C. Allen, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys. 64, 1045 (1992)

[N.1]

O. H. Nielson and Richard M. Martin, Phys. Rev. Lett. 50, 697 (1983)

[P.2]

M. C. Payne, J. D. Joannopoulos, D. C. Allen, M. P. Teter, T. A. Arias and D. H. Vanderbilt, Phys. Rev. Lett. 56, 2656

[P.3]

W. H. Press, B. P. Flannery, S. A. Teukolsky and W. T. Vetterling, Numerical Recipes, 1st ed, Chapter 10, Cambridge University Press.

[R.1]

A.M. Rappe, K.M. Rabe, K. Kaxiras and J.D. Joannopoulos, Phys. Rev. B 41, 1227 (1990)

[P.4]

R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press (1989)