溫度 與 波玆曼分佈
利用前面建立的知識,我們將推導出有名的 "波玆曼分佈",這是熱的物理學裏面的 key concept
(好像參加觀光團,每趟都有完整的行程。)
溫度當然關係冷熱,較冷的東西溫度較低。
但溫度也是有一個數量(數目字)的,此一數字的意義為何?(跳水、體操、疼痛感、昏迷指數,都是 1 到 10)
熱平衡
為回答上述問題,考慮將冷、熱物體接觸。上一章己討論過,能量會有流動,且經驗告訴我們一定由熱到冷。此過程(熱過程)中內含的能量及溫度都會有所改變。
一段時間後,當不再變化,謂之兩物體達成熱平衡。
看來似乎有不可逆的事情發生了。
熱過程決定了時間的方向(時間的箭頭指向達成熱平衡的方向)
如果幾個物體互相之間達成熱平衡,則它們的溫度也都一樣,此一觀念內藏在 "熱力學第零定律" 中
熱力學第零定律
分別與第三物達成熱平衡的兩物,互相之間也己達熱平衡。
雖標第零,但事實上最後提出,早期學者不認為需要這樣再多定一個定律。不過它倒提供了我們 "之所以" 可以使用溫度計來量溫度的學理基礎。
以與鎖定 "與溫度有關的物性",在熱平衡後讀取之藉以比較物體的冷熱,這就是溫度計。
溫度計能用,是熱力學第零定律的另一說法。
(各種)溫度計
要好用,其比熱需 遠低於 被測物體
一常見大類,用了液體膨脹的原理
量電阻也是一個方法,因為電阻對溫度敏感。如白金。
利用理想氣體方程式也是一法,但此法極低溫時因氣體會液化而失效
一個超低溫下常用的方法是液氣共存下量蒸氣壓
以上方法都有利用到對溫度敏感物性,但卻都不是線性的
拿什麼作標準?
十九世紀,卡諾引擎的觀念被提出
後來,人們發現可以用機率論的統計的方法來定溫度,這需要用到微觀態與巨觀態的概念,以下介紹
微觀態與巨觀態
區分微觀態與巨觀態,考慮以下範例
Ex 4.1 一百個銅枚有 n 個頭出現的機率(見課本)(速食店甩甩樂?)
呈現兩個關鍵點:
1. 系統由大量出現率相等的微觀態所描述
2. 我們實際上在量測的是系統 出現率不相等之巨觀態的性質(不同的巨觀態對應到不同數目的微觀態,因此機率不同)
系統在能量是 E 時的 微觀態有 Ω(E) 那麼多 ,而後者是一個很龐大的量。
微觀態構成巨觀態的遊戲規則
a system will appear
to choose a macroscopic configuration which maximizes the number of
microstates.
這是基於下列假設:
(1) each one of the possible microstates of a system is equally likely
to occur;
(2) the system's internal dynamics are such that the microstates of the system are continually changing;
(3) given enough time, the system will explore all possible microstates
and spend an equal time in each of them.(遍歷理論)
也就是說,
These assumptions imply that the system will most likely be found in
a configuration which is represented by the most microstates.
溫度之統計上的定義
系統 1 與系統 2 有熱接觸,但兩者一起隔離於環境之外,因此有
常數 = E = E1 + E2
Ω(E) = Ω1(E1)Ω2(E2)
最可能的 E1、E2 分割,是能使 Ω1(E1)Ω2(E2) 最大的那一組
找 d Ω1(E1)Ω2(E2) / dE1 : = 0 (極大時為零)
==> Ω2(E2) [d Ω1(E1)/ dE1] + Ω1(E1) [d Ω2(E2) / dE2 ] [ dE2 / dE1] = 0
但 E = 常數 = E1 + E2,故 dE2 / dE1= -1
同除以 Ω1(E1)Ω2(E2) 原式變為
[1/Ω1(E1)] [d Ω1(E1)/ dE1] - [1/ Ω2(E2)] [d Ω2(E2) / dE2 ] = 0
也就是
d lnΩ1(E1)/ dE1 = d lnΩ2(E2)/ dE2
定義
1/(kBT) = d lnΩ/ dE
其中 kB = 1.3807 × 10-23 KJ-1
思考:這是溫度?怎麼有這樣的鬼東西溫度?
前面談過,很多東西都可以做溫度計。當代的物理學家選了最理想的(理論)溫度計,然後乾脆將之定義為溫度。
上述定義中, Ω與 E 都沒有儀器可以直接量。
所以現在我們知道為什麼要定出第零定律了 (要在統計的理論框架下定溫度)
問題:給你一疊撲克牌,請你算它的溫度,可以嗎?不可以嗎?
系綜 (Ensemble)
Ensemble 的基本英文字義 :
We are using probability to describe thermal systems and our approach
is to imagine repeating an experiment to measure a property of a system
again and again because we cannot control the microscopic properties
(as described by the system’s microstates). In an attempt to formalize
this, Josiah Willard Gibbs in 1878 introduced a concept known as an
ensemble. This is an idealization in which one consider making a large
number of mental ‘photocopies’ of the system, each one of which represents
a possible state the system could be in.
三種
microcanonical :
ensemble 內的每一個 system 皆具相同固定的能量
subtle language : 既 "相同" , 又 "固定" ?
canonical ensenmble :
此一 ensumble 中每一個系統皆接與一熱庫交換能量, 其實 T will be fixed.
grand canonial ensemble
此一 ensemble 中每一個系統皆與一熱庫交換能量及粒子,系統之溫度與化學位勢恆定。
思考:Gibbs 提出了 ensemble 概念, 到底有什麼意義重大之處?
( 配合遍歷假說時, 有補捉到系統的行為。 )
Canonical Ensemble(正則系綜)
與前面一樣考慮獨立隔絕於外界的兩個互相連接系統,有固定總能 E (因為隔絕),只是此例中一個比另一個大非常多, 故分別有總能 E -ε 及 ε。系統能量 ε 不再是固定( E 是固定), 現在我們想知道這個能量是 ε 之小系統的機率。
我們先考慮假設系統一個能量值 ε 的一個微觀態 。(為什麼要作這個假設?為什麼可以作這個假設?) 則 系統 在此微觀態 (能量值 ε) 的機率是:
P(ε) ∝ Ω( E -ε) × 1
這個 ε 系統比 E -ε 的 系統(在此扮演熱庫)小很多,即ε << E
ln Ω( E -ε) = ln Ω( E ) - ε d ln Ω( E ) / dE + ...
將溫度的定義 d ln Ω( E ) / d E = 1/ (kBT) 引入上式,有
ln Ω( E -ε) = ln Ω( E ) - ε/( kBT ) + ...
忽略高次項就有
Ω( E -ε) = Ω( E ) e-ε/( kB T )
則配合一開始 P(ε) ∝ Ω( E -ε) × 1 ,就有
P(ε) ∝ e-ε/( kB T )
這就是有名的波玆曼分佈、正則分佈,而 e-ε/( kB T ) 則叫 波玆曼因子 (Boltzman factor)。
從函數的行為來看,溫度 T 時,系統能量小於 kBT 者有相當之機會出現。大於 kBT 者則出現機會少很多。
P (Er) = e-Er / ( kB T ) / Σi e-Ei / ( kB T )
這個分母 Σi e-Ei / ( kB T ) 叫作分配函數 (partition function)
Ex 4.2 電腦模擬自然產生波玆曼分佈(重要)
Step 1. 設整齊的初始分佈,每個位置均只一個量子。
Step 2. 隨機取兩位置,扣一量子加到另一位置去。
Step 3. 重覆第二步
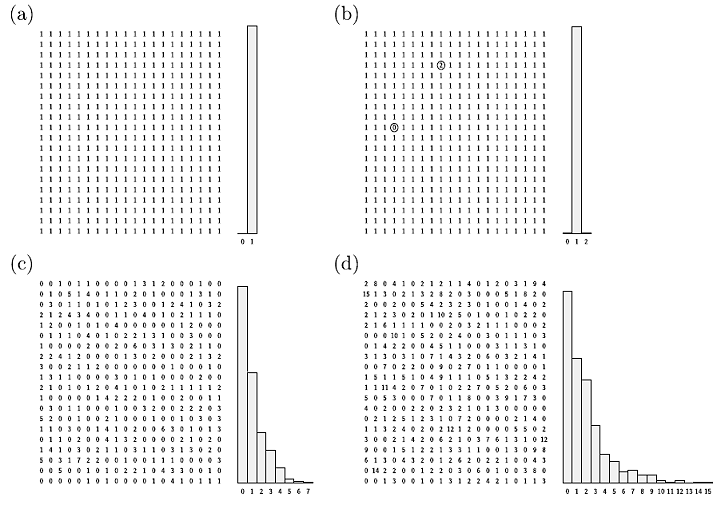
補充:http://comp.uark.edu/~jgeabana/mol_dyn/
思考:上面這個規則相當簡單的電腦模擬,為什麼會有這麼驚人的結果?而能呈現出波玆曼分佈的形貌。它到底抓到了什麼核心特徵?
提示:一個不斷交易的系統,被交換的量守恆,每個交換的個體機會均等。
問題:能量何德何能,可出現在波玆曼因子指數的分子上?
波玆曼分佈的應用
定義β ≡ 1/ (kBT) 以簡化書寫,也就是說
β = d lnΩ/ dE
Ex 4.3 最簡單的,雙態系統 (Two state system),注意高低溫極限
系統只有兩個微觀態,能量分別為 0 與 ε
求 P(0)、P(ε)、< E > 與溫度的關係
Ex 4.4 等溫大氣中,分子濃度隨高度之變化
n(z) = n(0) e-mgz/(kBT)
(打地鋪吸灰塵?)
Ex 4.5 加熱讓化學反應變快
活化能 Eact 的反應,其反應速率正比於 e-Eact/(kBT)
典型之 Eact 為 0.5 eV,則室溫下 加熱 10 度, 速率加倍。
Ex 4.6 太陽中心核融合
p+ + p+ → d+ + e+
E = e2 / (4πε0r)
e-E/(kBT) ~ 10-400
所幸有穿隧效應,使核融合仍得以發生。
