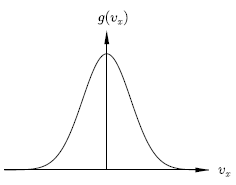
速度分佈的函數,某速度方向(定為 x)之 vx 到 vx + dvx 之間的數量分量是 g(vx) dvx ,不同的 vx 會表現出不同的 x 方向動能,基於波玆曼因子,指數上有相對的能量(為什麼是 相對的能量?)1/2 m vx2 ,故有
g(vx) ∝ exp [- m vx2 / 2 kB T ]
至於歸一化常數,則要求 ∫-∞∞ C exp[-mvx2/2kBT] dvx = 1
得(見課本)
g(vx) = √(m/2πkBT) exp[-mvx2/2kBT]
此一分佈函數馬上幫我們獲得下列期望值
< vx > = ∫-∞∞ vx g(vx) dvx = 0
< | vx| > = 2 ∫0∞ vx g(vx) dvx = √(2 kB T /πm)
< vx2 > = ∫-∞∞ vx2 g(vx) dvx = kB T / m
現在要選 v = | v | 到 v + dv 這範圍有多少個分子,
(為什麼這個數目字會和前面速度分量的不一樣?怎麼的不一樣法?)
球殼體積是 (注意這是速度空間)
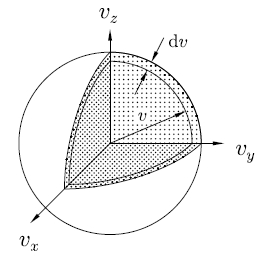
4πv2 dv
用 f(v) dv 表示 ,則
f(v) dv ∝ v2dv exp[-mv2 / 2 kBT]
此 f(v) 要滿足歸一化條件 ∫0∞ f(v) dv = 1,可定出(見課本 (5.11))
f(v) = 4/√(π) (m/2kBT)3/2 v2 exp[-mv2 / 2 kBT]
這稱為 Maxwell-Boltzman 速率分佈,或稱 Maxwell 速率分佈
< v > 及 < v2 >
使用 Maxwell-Boltzman 速率分佈,可得
< v > = ∫0∞ v f(v) dv = √(8 kBT / πm)
< v2 > = ∫0∞ v2 f(v) dv = 3 kBT / m
從 (5.7) 與 (5.14) 我們本來就有
< vx2 > + < vy2 > + < vz2 > = kBT / m + kBT / m + kBT / m = 3 kBT / m = < v2 >
再次確認無誤。
另外,均方根 root mean square 速率
vrms = √(< v2 >) = √( 3 kBT / m )
是正比於 m-1/2
一個氣體分子的平均動能
< EKE > = 1/2 m < v2 > = 3/2 kBT
上式說明,一個分子在氣體中的平均能量只與溫度有關。
速率分佈 f(v) 的極大值
使 f(v) 達最大的 v 可由解 df / dv = 0 而得
vmax = √( 2 kBT / m )
思考:與 vrms 比較一下,想想兩者意義 (非僅定義) 有何不同?
由於 √2 < √(8/π) < √3 ,故
vmax < <v> < vrms
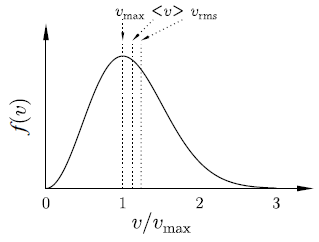
這是因為 Maxwell 速率分佈的尾部向右拖得很長。
Ex. 5.1 N2 分子的 vrms
(與聲速同一個數量級)
思考:這是巧合還是必然?


