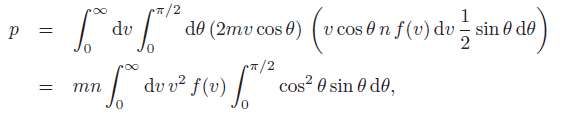壓力

 

壓力可說是氣體最基本（重要）的性質。水蒸氣壓力推動活塞促成了工業革命。

其單位是單位面積的受力（牛頓／米平方）。其他單位介紹，把課本看一看。

 

Ex 6.1 空氣密度約 1.29 kg m^-3，假設大氣密度均勻，估計大氣層厚度。

 

狀態方程式，描述物質之狀態函數間的關係。如以下形式：

p = f( T, V, N )

其中我們相當熟悉的一個，是理想氣體的狀態方程式

p = n k_B T

其中 n = N / V。

 

丹尼爾伯努力試著解釋波義耳定律（氣體 T 與 1/V 的關係），而引入在當時看來離經叛道的原子假說。

分子運動構成之形態的分佈

我們想知道，在平衡下，有多少分子，其速率是介於 v 與 v + dv 之間，且其方向是在 θ 到 θ+ dθ之間。

 

認識 固體角

角度如何由孤長與半徑定出？

θ  = s / r （見圖）

r 與 s 同步增大，角度不變

 

立體角

Ω = A / r²

全部範圍是 4πr² / r² = 4π

 

某速度、某方向飛行的分子數

如果分子沿任何特定方向的皆無偏好，則局限在 dΩ 固體角內的分量 (component) 為

dΩ/ 4π

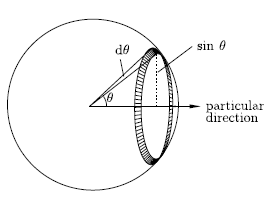
如果已定了某方向，則與該方向呈一夾角，涵蓋 θ到 θ+ dθ範圍的固體角大小（一條環）為

dΩ = 2πsinθdθ

因此，其立體角分量是

dΩ/ 4π  = (1/2) sinθdθ

也就是說，（擇定一方向情況下），每單位體積，將有

n f(v) dv (1/2) sinθdθ

這麼多的分子，其速率是介於 v 與 v + dv 之間，且其方向是在 θ 到 θ+ dθ之間。

 

擊中壁面的分子數

問題解析：

對某一壁面，有其法向量，來自不同之入射角之氣體流，對同一壁面的有效截面並不同，因此氣體數目就會隨角度的不同而不一樣。以下具體推導。

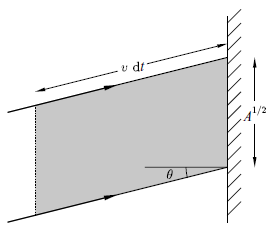
到目前為只，方向是任意指定。現在，把此一方向定為一個面積為 A 之壁面的法方向，見圖 6.5。

在小段時間 dt 之內 ，自角度θ飛來而能覆蓋到壁面 A 之分子流，其掃出來的體積大小為

A v dt cosθ 

（亦即角度越大，其有效體積越小）

拿這個體積，去乘上剛才前面得到之符合速率與角度之分子的分量，得

A v dt cosθn f(v) dv (1/2) sinθdθ

也就是說，單位時間內、撞擊到單位面積的，速率在 v 與 v + dv 之間，角度在 θ 到 θ+ dθ之間的分子總數是

v cosθn f(v) dv (1/2) sinθdθ

 

理想氣體定律 (方程式的導出)

我們現在準備計算壓力，關鍵是動量轉移。

對壁面入射角是θ的粒子，反彈後造成的動量轉移是 2 mv cosθ，乘上單位時間單位面積粒子數，

p = ∫₀^∞ dv ∫₀^π/2 dθ (2 m v cosθ) (  v cosθ  n f(v) dv (1/2) sinθ)

其中，用上了

∫₀^π/2   cos²θ sinθ dθ = 1/3

得

p = 1/3 m n < v² >

由 n = N / V

以及 < v² > = 3 k_B T / m

得

p V = N k_B T

或

p = n k_B T

 

由上式可看出，氣體壓力與氣體分子質量無關，只與溫度和單位體積有關。

 

Ex 6.2 一莫耳氣體在 STP 下佔有多少體積？

 

Ex 6.3 壓力與動能密度的關係為何？

 

道耳吞定律

氣體壓力為其各組成氣體之分壓和，即 p = Σ_i p _i ，以下證明：

基於 p = n kB T，

且

n = Σ_i n_i

便得證

p = Σ_i p _i

 

Ex 6.4 計算空氣中 CO2 的分壓。