分子逸散 / 溢瀉 (Effusion)

Effusion 指氣體從小孔由射出

 

Graham's Law of Effusion（與氣體分子質量平方根呈反比）

 

Ex 7.1 鈾 235 、238 化合物 UF₆ 分離

（綜合化學課聽到及內幕：師大鈽實驗室）

 

Ex 7.2 氦氣、氮氣逸散比較

 

Flux （流）

可以是質量流、能量流或動量流。

本章談分子流，定義為 "分子流 = 分子數/ (面積 × 時間）"，即單位面積、 單位時間流過的分子數。

從前章 "撞擊到壁上的" 速率分佈函數 p.58 (6.13) 出發，但僅積分所有向前方向的分子，而沒有像壓力一般含動量轉移 2 mv cosθ 的部分

Φ = ∫₀^∞ ∫₀^π/2   v cosθ  n f(v) dv (1/2) sinθdθ

得（積分上式利用到了 ∫₀^π/2    sinθ cosθ dθ= ∫₀^π/2    sinθ dsinθ= ∫₀¹ u du = 1/2）

Φ = (1/4) n < v >

 

另一種表示法，上式再利用 p = n k_B T、< v > = √(8 k_BT/πm) 代入，得

Φ = p / √(2π m k_BT)

可以清楚見到 √m 反比的形式 。

 

Ex 7.3  計算 N₂ 在 STP 之粒子流

 

Effusion

Ex 7.4 Knudsen 方法量蒸氣壓

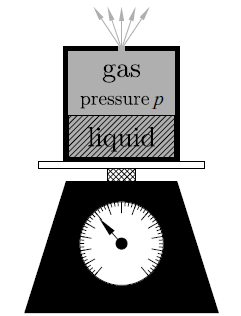
在  dt 時間內

effusion rate 是 Φ A

dM /  dt = m Φ A = m p A / √(2πm k_BT)

得

p = √(2πk_BT/m) (1/A) [ dM /  dt ]

 

Effusion 偏好比較快的原子，因此逸散出來的分子其速率分佈並非 Maxwell 分佈，這是因為速度快的分子撞擊數也增多之故。（勿因來自同一已平衡容器之氣體便覺奇怪，作者以出國觀光者的代表性為例。 ）

我們也可由 "單位面積的碰壁(通過)分子" 會比同樣 "具有 v, θ 條件的分子數" 多了 v 因子 (為什麼不說是v cos θ因子？) 而理解新的速率分佈函數也應是有多了一個 v 的

v³ e^{-mv2 / 2k_BT}

與 Maxwell 分佈比較如下：

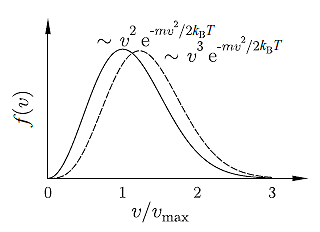
在 Maxwell 分佈 中的氣體其平均動能為

1/2 m <v²> = 3/2 k_B T

來自 effusion 的 氣體則還要更高，見下例

 

Ex 7.5

<kinertic energy> = 2 k_B T

 

Effusion 自然要小洞才能發生，開了拳頭大的洞就無所謂逸散了。那到底洞必須要多小才有 effusion 效應 ？答案：洞的直徑須遠小於氣體分子的平均自由路徑。（詳見第八章）

 

Ex 7.6 考慮容器中隔分開但上有小洞直徑 D

D >> λ, p₁ = p₂

D << λ, Φ₁ = Φ₂

利用 (7.9) 的結果， 可得

p₁ / √T₁ = p₂ / √T₂

 

 

最後，估計低溫下氣體沿著管子延伸的流動（速）率：

 

Ex 7.7 長 L、直徑 D 的管子，兩頭壓力差是 p₁ - p₂ ，問極低壓下的氣體流速。

（為何要強調是低壓？）

氣壓低 平均自由徑 才長 管徑才能適用 effusion

思考關鍵是：

需要密度梯度 (亦即壓力梯度)

x 處的淨流量，

Φ(x) ~ 1/4 < v > [ n(x + D) - n (x - D) ]

為什麼出現這個 D 的深度？

說明：截面直徑大小為 D 之管，（考慮與其他氣體分子碰撞的機會遠小於與管壁碰撞的情形），通過 D 截面之分子其上一次（與管壁）的無碰撞自由飛行範圍是 D 的深度。（若不是這樣，代表分子在飛行方向上有偏好， 這是不合理的。）

套用 p = 1/3 n m < v² >

改寫為以壓力表示

Φ(x) ~ 3/(4m) (< v > / < v² > ) [ p(x + D) - p(x - D) ]

其中我們可以把 p(x + D) - p(x - D) 寫為

p(x + D) - p(x - D) ~ -2D dp / dx

又加上考慮 stady state 已達到，流量處處恆定，即

dp/dx = (p₁ - p₂) / L

 

基於質量流率 (mass flow rate)

dM/dt = m Φ A = m Φ (π D² / 4)

因而有

dM/dt ~ (3/8) (< v > / < v² >) π D³ (p₁ - p₂) / L

再使用

< v >² / < v² > = 8/(3π)

得到最後的結果是：

d/dt M ~ ( D³ / < v >  ) [p₁ - p₂] / L

 

請注意這個 D³ ，代表越細的管，欲達相同流量，難壓很多（壓力三次方大才彌補得過來）。

另外，它是怎麼來的？D² 來自管的截面積，還有一個 D 來自有效的自由飛行深度。如下：

思考：管的兩端壓力不一樣，這怎麼可以，少了的壓力跑到那裡去了？

(氣流穩定之後，兩端流入與流出的分子數量要一模一樣。但 P = n k_B T