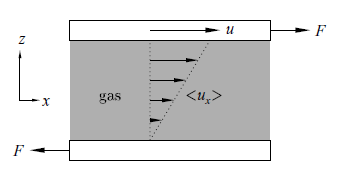
黏滯性是描述液體對剪應力產生之形變的抵抗力。
對直線、平行、均勻流,層間剪應力是 "正比於" 垂直流場方向上的 "速度梯度"。(這是一種近似)
Key concept : 橫向的流速差梯度
黏滯係數 (coefficient of viscosity) η 定義為 :
剪應力 (sheer stress) τxz = F / A 與流速(差)梯度 d ux / dt 之間的比例係數
τxz ≡ F / A = η d ux / dt
這裏我們談的流體是氣體,因此 ux 還要再加上平均的效應 < ux > (氣體分子的速率遵守 Maxwell-Boltzman 分佈)
(我們還是期待此一氣體不離平衡太遠,雖說本章一開始即言明傳輸現象不是平衡的系統。)
依此定義,想推導:
x-方向的動量,沿 z 方向(穿透)傳輸的程度
(聯想:不倒翁鎚遊戲)(對於理想氣體,這種效應來自何處?)

用 x 方向動量流(是 z 的函數,故予下標 z)表示出來,將會是
Πz = - η ∂< ux > / ∂z
以下估計動量流 Πz 與∂< ux > / ∂z 的關係:
由氣體動力論的觀點,來估算 x 方向動量流,切入點如下:
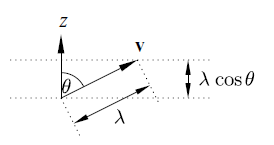
思考 :z 處的分子流為何有能力 "帶動" 到 z + Δz 處之橫向動量變化?
觀點:分子斜著飛,在碰撞前位置到達了 Δz,也自然把自己的 vx 貢獻給了 z + Δz 處,而產生帶動橫向動量變化的效果。
與法方向夾角θ的分子,其 " 向上" 平均自由路徑(的投影)為 λcosθ
則這些偏向上飛行夾角θ之分子將會夾帶的 x-方向動量是
- m (∂< ux > / ∂z ) λcosθ
注意此處 λcosθ之角色為 Δz ,透過乘積 (∂< ux > / ∂z ) Δz 來取得 Δ< ux >,因此上列者確實為(x 方向)動量變化。
以此去積分角度、速率,得總的動量流:
Πz = ∫0∞ ∫0π v cosθ n f(v) dv 1/2 sinθ dθ · m (- ∂< ux > / ∂z ) λcosθ
= 1/2 n m λ∫0∞ v f(v) dv (- ∂< ux > / ∂z ) ∫0πcos2θsinθdθ
= - 1/3 n m λ < v > (∂< ux > / ∂z )
(問:在此的推導,λ為何與 v 無關?)
(討論:訂出 λ(v) 會不會更好?)
得出
η= 1/3 n m λ < v >
(討論:這是氣體,那液體呢?)
定義導熱係數
Jz = - κ (∂T /∂z )
向量形式
J = - κ∇T
為了推導 κ,思考:分子 如何攜帶能量?答案是動能。
< 1/2 m v2 > = 3/2 kB T
上式可看成是單原子分子的比熱,僅有移動動能,不含轉動及振動動能的部分。為了使之後推導的結果適用於單、雙原子分子,以下用分子熱容而不把 < 1/2 m v2 > 拆開融入公式中處理 。
因此,從比熱的角度看
Cmolecule ΔT = Cmolecule (∂T /∂z ) Δz = Cmolecule (∂T /∂z ) λcosθ
熱流為 ( )
Jz = ∫0∞ dv ∫0π [-Cmolecule (∂T /∂z ) λcosθ] v cosθ n f(v) 1/2 sinθ dθ
= - 1/2 n Cmolecule λ∫0∞ v f(v) dv (∂T /∂z ) ∫0π cos2θsinθ dθ
= - 1/2 n Cmolecule λ< v > (∂T /∂z )
因此
κ = 1/3 CV λ< v >
假設 n* 是加了記號的分子密度 (為什麼要如此設?)
一個區域若有粒子密度的不均勻性(即梯度),則自然界便會發生淨粒子流,以企圖達到最終之平衡(等分佈),而擴散係數 D 則決定此一過程之快慢程度。
以下先具體的寫出此係數 D 與其他物理量之間的關係:
首先,濃度梯度的存在,造成粒子流出的流量 Φz 為
Φz = - D (∂n*/∂z)
現在,考慮面積 A、厚度 dz 的一片 Slab ,我們要估對進入 A 這一個片體積之中
在 z 處流入的粒子流率 A Φz
在 z + dz 處流出的粒子流率 A [(Φz + (∂Φz /∂z) dz ]
兩者差,即區域內部粒子密度之增加
∂(n* A dz) /∂t = - A (∂Φz /∂z) dz
∂n* /∂t = - ∂Φz /∂z
把最上面 Φz 與 ∂n*/∂z 及關係代入後,得到
∂n* /∂t = D ∂2 n* /∂z2
這就是所謂的 "擴散方程式" (diffusion equation)
(三維形式擴散方程式之推導見課本。)
註:擴散方程式可由連續方程式來得到,這是因為粒子(或質量)不滅的基本設定。反之,前兩節中探討的熱流與動量流,就沒有不滅的特性,因此沒有對應的連續方種式。
從氣體動力論出發來推導出擴散係數 D 的方式如下:(思考邏輯與前面各量一模一樣)
已知 D 的定義 Φz = - D (∂n*/∂z) ,另由 動力論 估計 Φz,藉著 Δn* = (∂n*/∂z ) dz = (∂n*/∂z ) λ cosθ,故有
Φz = ∫0∞ v cosθ f(v) dv 1/2 sinθ [ -(∂n*/∂z ) λ cosθ]
= -1/3 λ < v > ∂n*/∂z
故
D = 1/3 λ < v >
D 的特性(見課本整理)
D ∝ p-1
D ∝ T2/3
D ∝ η
D ∝ m-1/2 d-2
D = 2/(3πnd2) (kBT/πm) 1/2
問題:以上是氣體的,那液體(布朗運動)呢?
愛因斯坦論文
http://hermes.ffn.ub.es/luisnavarro/nuevo_maletin/Einstein_1906_thesis.pdf
http://www.scribd.com/doc/11460732/a-New-Determination-of-Molecular-Dimensions-2


