球極座標下,Laplacian 算子為
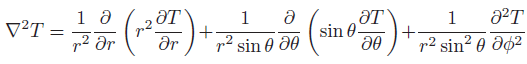
若是球對稱,則減化為
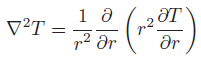
Ex 10.2 球體 steady state 的溫度解
(1/r2) (∂/∂t) (r2∂T/∂r) = 0
考慮若 T 與 r 無關 ∂T/∂r = 0 會成立一個解
又 若 r2∂T/∂r 與 r 無關,則(∂/∂t) (r2∂T/∂r) = 0 又 會成立一個解
故,T = A + B / r
其中 A、 B 是常數
Ex 10.3 球狀雞進烤箱
想知道雞球中心溫度隨時間的變化。
熱擴散方程式
前章已利用動力論導出氣體的熱傳輸行為。本章要介紹求解物質熱傳導性有關及行為。解法基本上是在十八世紀末、十九世紀初一些數學家所提出的解法。
溫度對物質物性有重要的影響。在此關鍵方程式,是描述熱擴散,也就是熱流如何在不同環境之下,從一個地方 "擴散" 到另一個地方。
我們想要知道,溫度隨著空間與時間變化的 "溫度場",以及其中之能量的流動。本章以介紹這些解題方法為主。
熱擴散方程式的推導獲得
回憶前章學過熱流與溫度梯度的關係,
J = -κ∇ T
又粒子流也有
Φ = - D ∇n
此外,電流與電場(電位梯度)也有類似的關係:
Je = σE = -σ ∇ φ
以上問題於數學形式如出一轍,因此解的數學也形式也相同。
事實上所有方程式,都源自於能量、粒子、電荷的不可消滅性。(因此有些書是以連續方程式當作切入點來分析這個問題及建立方程式。)(但本章僅處理熱)
流出封閉面 S 的總熱量是
∫S J · dS
流失的熱(流率),表現在封閉面體積內降溫,
(∂ / ∂t ) ∫V CT dv
其中 C 是熱容。
從發散定理,
∫S J · dS = ∫∇·J dv
因此我們有
∫∇·J dv = - (∂ / ∂t ) ∫ CT dv
= -∫ (∂ / ∂t ) CT dv
= -∫ C (∂T / ∂t ) dv
如此得到
∇·J = - C (∂T / ∂t )
再把前面 J = -κ∇ T 代入換掉 J ,就得一全 T 之方程式
-κ ∇· ∇ T = - C (∂T / ∂t )
即
∂T / ∂t = D ∇2 T
其中此處之 D 為 κ/ C (稱為熱擴散率)
一維熱擴散方程式
∂T / ∂t = D ∂2 T / ∂x2
Ex 10.1 一維熱擴散方程式的解
見課本詳解
正弦溫度波透入地面的溫度分佈情形
通解
T(x,t) = Σω A(ω) e(-iωt) exp[(i-1)√(ω/2D) x]
邊界條件,假設正弦變化(日夜溫差或冬夏溫差)
T(0,t) = T0 + ΔT cosΩT
此一邊界條件可進一步改寫為
T(0,t) = T0 + 1/2 ΔT eiΩt + 1/2 ΔT e-iΩt
原通解在 x = 0 處為
T(x=0,t) = Σω A(ω) e(-iωt)
與邊界條件比較得
A(0) = T0、 A(-Ω) = ΔT/2 、 A(Ω) = ΔT/2
因此解(對 x ≥ 0 而言)為
T(x,t) = T0 + ΔT/2 cosΩT e-x/δ cos(Ωt - x/δ)
其中
δ = √(2D/Ω) = √(2κ/(ΩC))
叫作趨膚深度 (skin depth)
此解有以下特性
溫度穿透力衰減 e-x/δ
相位偏移 x/δ
變化快的衰減快 δ ∝ Ω-1/2
問題:為什麼地窖冬暖夏涼?
The Steady State 靜態(解)
系統達成 Steady State 時,各狀態皆不隨時間改變,溫度亦然。
亦即
∂ T / ∂ t = 0
故 熱擴散方程式 成為
∇2 T = 0
即 Laplace 方程式。
球對稱的熱擴散方程式
球極座標下,Laplacian 算子為
若是球對稱,則減化為
Ex 10.2 球體 steady state 的溫度解
(1/r2) (∂/∂t) (r2∂T/∂r) = 0
考慮若 T 與 r 無關 ∂T/∂r = 0 會成立一個解
又 若 r2∂T/∂r 與 r 無關,則(∂/∂t) (r2∂T/∂r) = 0 又 會成立一個解
故,T = A + B / r
其中 A、 B 是常數
Ex 10.3 球狀雞進烤箱
想知道雞球中心溫度隨時間的變化。
牛頓冷卻定律
J = h ΔT
溫差決定這熱流量 (接觸面也是)
Ex 10.4
-C ∂ T / ∂ t = J A = h (T - Ts)
解 : 溫度以指數方式下降
補充:彭巴 (Mpemba) 效應
Prandtl number
對流有多重要?比起傳導?
kinematic viscosity ν = η / cp
thermal diffusivity D = κ / ρ cp
σp = ν/ D
熱源
若有單位體積熱源 H ,則熱流的散度充會變成
∇· J = - C ∂T/∂t + H
則方程式變為
∇2 T = (C/κ) ∂T/∂t + H/κ
或是
∂T/∂t = D∇2 T - H/C
Ex 10.5 兩端冷卻,整個通電發熱金屬棒達steady state 後中點的溫度。