熱引擎（熱機） 與 第二定律

 

前言（為了要建立觀念的一致性，特加註此段）

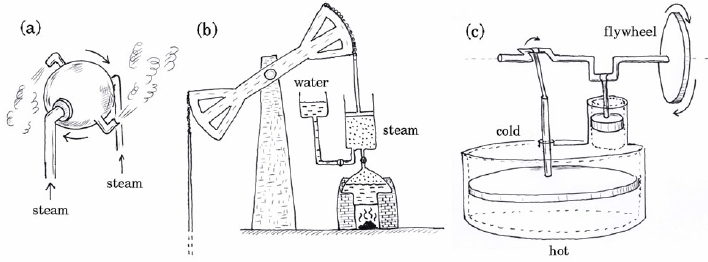
氣體理論（理想氣體方程式）的成功，讓卡諾得以提出簡明的理想引擎，它有兩個最重要的特性：(1) 其由溫差造成熱流中，作功的比例是是可以精確解析計算的，(2) 由於全由可逆過程組成循環，因此也可以反轉。

卡諾引擎之可以反轉的特性，使卡諾可以提出冷、熱機結合的想像實驗。使用"熱不會自動由低溫處流向高溫處" 的常識，推得了 "沒有任何引擎（注意引擎的定義）的效率可以超過卡諾引擎者（事實上是所有可逆者）" 這樣的一個重大的規律。此一觀念催生了熱力學第二定律的建立。

第二定律有好幾種陳述，透過 T 字型熱功三叉路 的有用圖像，可以證明它們都是等效的。

而此一陳述／定律尋求數量化的過程時，便帶出了熵的定義。

 

本章比較長，其架構如下：

第二定律（含不同陳述）

卡諾引擎及其效率

卡諾定理

克勞休斯、凱爾文陳述的等效性

熱機例

反轉運行的熱機

克勞休斯定理

 

 

 

熱力學第二定律

(緣由：所有的觀察皆指出，熱是從高溫物體流至低溫物體。)

 

克勞修斯 (Clausius) 陳述：

只把 heat 從 cold 物體 轉移到 hot 物體的過程，不可能發生

 

凱爾文 (Kelvin) 陳述：

完全把熱轉成為作功的過程，不可能發生

 

 

卡諾引擎

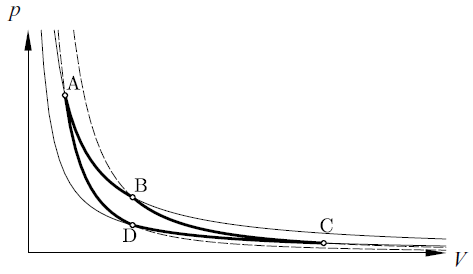
上面 A-B、C-D 是等溫線；A-D、B-C 則是絕熱線。

 

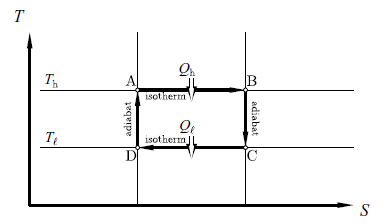
W = Qh - Ql

 

Ex 13.1 將理想氣體進行卡諾循環的熱流比 Qh / Ql ，以溫度比 Th / Tl  表示出來。

利用前章 12.2 的結果，

A → B : Qh = RTh lm (VB / VA)

B → C : Th/Tl = (VC / VB)γ-1

C → D : Ql =  - RTl lm (VD / VC)

D → A : Tl/Th = (VA / VD)γ-1

上四式中的第二、第四式導致

VC / VB =  VD / VA

移項得

VB / VA = VC / VD

前四式中的第一式除以第三式，並置換掉體積比值，導致

Qh / Ql = Th / Tl

這樣的一個關鍵的結果。

 

卡諾引擎之熱流與作功的示意圖

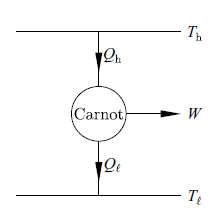
其效率的定義

η ≡ W / Qh

η永遠是一個比 1 小的值，因為所作的功 W 不可能大過 提供的熱量 。

 

Ex 13.2 卡諾引擎的效率

ηCarnot = (Qh - Ql) / Qh

使用 (13.7) 即理想氣體進行卡諾循環：有 Qh / Ql = Th / Tl，得

ηCarnot =  (Th - Tl) / Th  = 1 -  ( Tl / Th  )

 

真實引擎比起卡諾引擎的效率又低了不少，見下例：

Ex 13.3 渦輪發電機

卡諾(理想極限) 60%、實際 40%。

 

卡諾定理 (13.3)

事實上，卡諾引撉有最高的引擎效率（引擎效率的定義見上），這是一個定理。

卡諾定理

所有連接兩個溫度（熱庫）之間運作的熱機，其 (引擎) 效率不會超過卡諾引擎者。

 

問題：卡諾引擎的效率之公式形式 1 -  Tl / Th  到底有什麼奧妙之處？ 何以僅這樣就已經是最高可能的效率？

 

此定理的證明，可基於克勞修斯陳述，用反證法，巧妙地把一個效率更高的引擎用來反轉卡諾引擎：

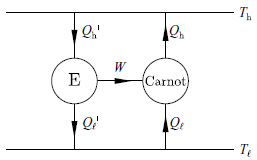
如果存在 E 比 Carnot engine 效率更高，即

ηE > ηCarnot

即

W / Q'h > W / Qh

因而

Qh > Q'h ，也就是說 Qh - Q'h > 0

另外，基於熱力學第一定律，

W = Q'h - Q'l = Qh - Ql

Qh - Q'h  = Ql - Q'l

從上面 Qh - Q'h > 0  因此上式等號左邊為正，故等號右邊也是。

但我們仔細看這個 Ql - Q'l 相當於自低溫熱庫 Tl 所抽走的熱量，如果它可以是正的，代表熱力學第二定律己經違反。

（上述的巧妙證明，是卡諾所提出，才催生熱力學第二定律。在未有該定律的當年，卡諾以低溫送熱到高溫有違常識，來確立論點。）

 

餘定理

所有的可逆引擎皆有相同的效率 ηCarnot

證明：

想像易外一個可逆引擎 R，基於卡諾定理 ηR ≤ηCarnot 。我們將它逆轉並像下圖那樣接上一個卡諾引擎。

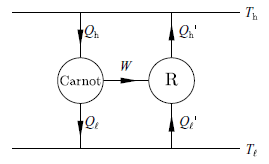
此一架講將會造成熱從低溫傳到高溫的淨效應，因此違反克勞修斯陳述（第二定律），除非其效率不是小於而是相等。如此得證。

 

 

克勞修斯與凱爾文陳述的等效性 (13.4)

證明策略：違反 C 則違反 K； 違反 K 則違反 C 。

 

 

幾個熱機（引擎）的例子 (13.5)

（詳見課文介紹）

Hero's 引擎

 

Newcomen's 引擎

瓦特改良它而促進了工業革命的發生

 

Striling's 引擎

 

內燃機

 

 

逆轉的熱機 (13.6)

(1) 冷 (凍) 機（Refrigerator、frig）

作功將熱從（通常是）低溫處移走。

效率定義 η = Ql /  W

若使用卡諾引擎來做， η = T l /  (T h - T l )

 

問題：冷 (凍) 機效率可不可以超過百分之百？不會不合理嗎？

問題：冷 (凍) 機效率可不可以是負的？即是否一定必須 T h > T l？

 

(2) 熱泵 ( Heat pump )

作功將熱移入（通常是）低溫處。

效率定義 η = Qh /  W

若使用卡諾引擎來做， η = T h /  (T h - T l )

注意效率永遠大於 100%

補充：汽車及住宅用二合一型冷暖氣機。

 

克勞修斯定理

對卡諾循環而言，固然熱流 Qh  進 (+)、 Ql  出 (-)，熱量並不守恆，但是基於 Qh/Ql = Th/Tl 特性， 有 Qh / Th = Ql / Tl ，也就是說 ΔQ / T 這個量，加總起來（流出帶負號），在一個循環後是守恆的，如下：

Σcycle ΔQrev/T = Qh / Th +  (-Ql)/ Tl = 0

換成積分符號的話

∫cycle đQrev/T = 0

（物理學一貫的目標就是在找守恆量，我們在這裏看到一個了嗎？還是只找到了一個狀態函數？）

 

我們在此之前，僅用卡諾引擎。以下我們想探討一個比較真實的情況，即 (1) 作功之物體一刻系列溫度而非僅兩個。(2) 另外則是，不一定可逆。

假設我們現在有一個循環，在某個過程點 i 上，其熱的進入 đQi （可以是負，後面說明），且當時系統連接到的熱庫是 Ti （如下 (a) 圖），

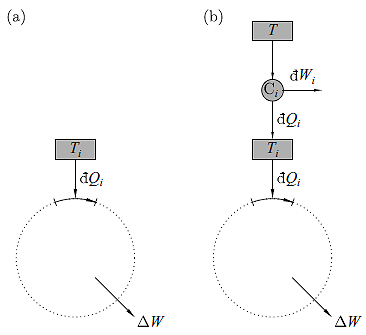
則由於是一個循環的關係，內能繞一圈後不變，而不同階段 i 進進出出的正負總合就等於作功。故基於第一定律本來就有，總功為：

ΔW = Σi đQi

接下來，要把整組機械系統浸在溫度是 T 的環境中，並用最有效率的卡諾引擎收集餘熱作功。想像每個過程點 i 的熱流 đQi 各是由一個連接在溫度 T 及 Ti 熱庫的卡諾引擎所提供（如上圖 (b)）， 而這些 T 熱庫則是全部又接在一起 （為什麼要這樣想？）<管控熱庫，儘可能防止熱耗散>，如此，

我們可以寫下各過程點的卡諾引擎作功 đWi ，基於卡諾引擎

"熱流入 Ti 熱庫" / Ti = "熱流出 T 熱庫" / T ，即

đQTi / Ti =  đQT / T

再加上，我們有 đQT = đQTi + đWi，故得

đQTi / Ti =  (đQTi + đWi)/ T

此 đQTi  事實上在本例中就是 đQi ，故上式變成

đQi / Ti =  (đQi + đWi)/ T

即

đWi = đQi (T / Ti  - 1)

（在此導出了待會要用的關係式）

我們可看出以上(b) 圖考量的系統，能夠把全部的熱都拿去作功，如此違反了第二定律（違反 Kelvin 陳述），因此上面的結論不可能成立 。

問題：錯誤的前提所推得的結論一定是錯誤的嗎？

（其實，此處課文的邏輯架構是：完全熱轉功之總功已算出，假設大於零，則違反第二定律）

因此上述想像機械總功不是真的可以拿到的，即數學上不可以為正，如此導致 "每個循環的總功" = ΔW + ΣcycleđWi ≤ 0

前有ΔW = Σi đQi，代入，再加以把 đWi 寫成 đQi (T / Ti  - 1) ，我們因此有

T Σcycle đQi / Ti  ≤ 0

由於 T > 0，我們於是得到

Σcycle đQi / Ti  ≤ 0

寫成積分式則成為

∫C đQ / T  ≤ 0

 

Clausius' Theorem 總結如下：

對任何封閉循環，∫C đQ / T  ≤ 0 ，其中等號在其為可逆時成立。

（證明就是前面的敘述）

 

Ex 13.5 兩個具固定熱容值之物體作為熱庫所構成的卡諾循環 （舊版課本沒有）