熵
作業:Entropy 這個字是怎麼來的?
作業:中文翻譯為何叫 "熵"?
熵 (在熱力學上) 的定義
前章有 ∫C đQrev / T = 0 ,這等效於說積分量∫AB đQrev / T 與路徑無關,因此 đQrev / T 是一個 exact differential。我們可將之定義為一個狀態函數叫作"熵"
dS ≡ đQrev / T
使得
S(B) - S(A) = ∫AB đQrev / T
而此 S 是一個 狀態函數。
對於一個可逆絕熱過程, đQrev = 0,因此熵也就不會改變 (叫 isentropic 過程)。
不可逆變化(熵增原理)
熵 是藉由可逆的熱改變 來定義。由於熵是狀態函數,因此積分任何一個迴路其結果為零。
∫C đQrev/ T = 0
另外,從克勞修斯不等式,則有
∫C đQ / T ≤ 0
(請注意兩者不同之處,在可逆與否)
假設一迴路 A ---> B 是不可逆而 B == > A 則是可逆,則有
∫AB đQ / T + ∫BA đQrev/ T ≤ 0
即
∫AB đQ / T ≤ ∫AB đQrev/ T
上式積分不論範圍多小皆成立,故有
dS = đQrev / T ≥ đQ / T
對於絕熱的系統, đQ = 0,上式便成
dS ≥ 0
事實上,這是熱力學的第二定律的另一種陳述(別忘了前提是絕熱),"孤立系統的熵趨於最大"。
(思考:得出上面 "封閉系統之熵永遠增加" 之重要結論,我們當然是用上了前面已證明過的克勞修斯定理。然而,有無直接/思考觀察 dS = đQrev / T 中各量的變化行為, 而也能讓我們感受到閉系統熵為什麼只能增加的方式?)
問題:像詭論一般地,若我們把上述推導之迴路命名順序對調,定成 "迴路 A -> B 是可逆而 B -> A 則是不可逆",則有
∫AB đQrev / T + ∫BA đQ / T ≤ 0 (1)
或
∫BA đQ / T + ∫AB đQrev / T ≤ 0 (2)
上式 (1) 便整理成
∫BA đQ / T ≤ - ∫AB đQrev / T
∫BA đQ / T ≤∫BA đQrev / T
đQ / T ≤ đ Qrev / T
但也可寫成
∫AB đQrev / T ≤ -∫BA đQ / T
∫AB đQrev / T ≤∫AB đQ / T
đQrev / T ≤ đQ / T
怎麼會有這種事!
(有同學說:不可逆過程的積分-∫BA đQ / T 不可以被改成 ∫AB đQ / T。是這樣嗎?)(畢竟,之前是採用了卡諾引擎是可逆才可倒轉的事實,才建立第二定律相關觀念的啊。)
那為什麼不能倒轉的系統,不能作上下限交換的動作?(微積分課本裏上下限可交換得負之性質,難道不是證明出來的嗎?)
是狀態函數的量,放在迴路積分裏,總結果才會保證是零。
如果任何 -∫BA f dx 都等於 ∫AB f dx,這將導致 ∫C f dx = 0 永遠成立,與路徑無關,即不管什麼 f dx 都可寫成全微分(狀態函數)dF,這明顯是不對的。從這個角度看,只有被積分的函數是狀態函數,才有機會讓此上下限交換後變為為負的性質成立。(不同路線,在微積分學就是不同的積分。)
但若是 A -> B 與 B -> A 是同一條線,只是路線相反,可不可以?
是同一條路線當然可以,但請注意,畫在狀態函數座標圖上的線,都是可逆的過程吧?不可逆者在此圖上標示得出來嗎?可逆性與達平衡之間的關係要回想一下。
(能不能舉出,數學上 -∫BA f dx ≠ ∫AB f dx 的例子?)
(問題:在以狀態函數為座標的平面上所畫出的線,都是可逆的嗎?不然,為何會有自由膨脹在 p-V 圖上是畫不出曲線的說法?沿著線上的每一點,系統都有達成熱平衡,就是可逆嗎?可逆過程要成立的條件是什麼?)
小複習:畫在狀態函數座標圖上的線,都是可逆的過程,不可逆者在此圖上是標不出來的。可逆性過程定義上的要求,即變化中的各鄰近點間之皆達平衡。
不可逆過程的物理量積分,在相圖上表示不出來,但積分結果仍是有意義,只不過
(1) 不能再套用微積分裏上下限對調得負號的作法。
(2) 不能把積分拿掉。(與歷程有關,無全微分型反導數)
應用到宇宙
假設宇宙是一個孤立系統,則熱力學第一與第二定律對其描述如下:
(1) UUniverse = 常數
(2) SUniverse 只會增加
(延伸:黑洞的問題)
Ex 14.1 接了大熱庫的小系統(要驗證不論熱流方向為何,熵總是增加)
(藉此體會或感受熵是怎麼只增不減的。)
再談第一定律
新定義的量:熵,讓我們更優雅地且有用地表達出第一定律。
本來是
dU = đQ + đW
dU = đQ - p dV
由於建立了
僅對可逆過程而言,
đQ / T = dS
而有
đQ = T dS
以及
đW = -p dV
因此
dU = T dS - p dV
注意,現在全部都是由狀態函數所表示出來,與路徑無關,這表示,推導過程中雖強調是可逆過程,但此公式對不可逆者也一樣成立!(好像變魔術一樣。)
對不可逆過程而言, đQ ≤ T dS (比可逆時多了微觀態)且 đW ≥ -p dV (功浪費,未全用在推動活塞上),但 dU 值還是與可逆者是一樣的。
問題:p dV 是作功 dW,V dp 是什麼?(該不會也是作功吧?)
上式 dU = T dS - p dV 不管對什麼過程都成立,蘊藏的一個訊息是,微變量的 U(即 dU)隨著 微變量 dS 與 dV 而變化,S 與 V 是 U 的自然變數。它們都是 extensive (外延) 變數,與體積大小有關,而 T 與 p 則較像力一般是強度性的東西,叫 intensive 變數。
事實上,從數學的角度我們期待
dU = (∂U /∂S )V dS + (∂U /∂V )S dV
我們也就因此確認了
T = (∂U /∂S )V
p = - (∂U /∂V )S
這兩個關係式。
不但如此,連 p/T 比例,也可得自
p / T = - (∂U /∂V )S (∂S /∂U )V = (∂S /∂V )U
這裏面我們使用了倒轉定理 (reciprocity theorem) (詳見課文 C.42)。
Ex. 14.2 預測兩個系統間傳遞內能及傳遞體積而達到平衡的情況(條件)。
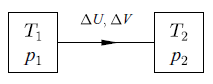
T dS = dU + p dV
dS = (1/T) dU + (p/T) dV
對本例中的兩個系統向熵總和而言
ΔS = (1/T1 - 1/T2) ΔU + (p1/T1 - p2/T2) ΔV
閉封系統之熵永遠增加,直到 ΔS = 0,這意味著 ΔU 及 ΔV 皆可自由改變的情況下,直到 T1 = T2、 p1 = p2 才會停止(達平衡)。
整理
dU = đQ + đW (總是對)
đQ = T dS (僅可逆過程適用)
đW = -pdV (僅可逆過程適用)
dU = T dS - p dV (總是對)
對不可逆過程而言, đ S ≤ T dS 、 đW ≥ - p dV
焦耳膨脹
本節仔細討論一種不可逆過程,叫做焦耳膨脹(有些書稱作自由膨脹)。一開始左邊氣室有氣體,右邊抽真空。之後一瞬間開啟閥門,讓氣體在絕熱的情況下,快速達到平衡的狀態。
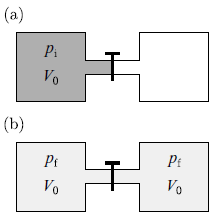
基於理想氣體方程式
pi V0 = R Ti
焦耳膨脹後
pf (2V0) = R Tf
全程絕熱所以 ΔU = 0 ,而對理想氣體而言 E 只與 T 有關,故
Ti = Tf
這表示
pi V0 = pf (2V0)
即
pf = 1/2 pi
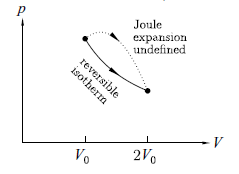
p 與 V 在膨脹過程中 之意義並不明確,因並這不是一個平衡過程 。所幸(我們之後所真正要的)熵是一個狀態函數,其積分本來就只與頭尾有關,因此我們可以改動積分之路徑,而選擇一個好算者。用一條等溫線(可逆)來連接初、末態,又因為等溫的理想氣體其內能相同,故有 dU = 0, 故
dS = dQ/T = p dV / T
如此造成
ΔS = ∫if dS = ∫if dQ / T = ∫if p dV / T = ∫V02V0 R dV / V = R ln 2
此熵的增加 R ln 2 就是焦耳膨脹的熵改變。
p 與 V 是不是狀態函數?
Ex 14.3 宇宙內有一團氣體作焦耳膨脹的熵計算
一個關於焦耳膨脹的詭論?
1. 焦耳膨脹是絕熱的,故 ΔQ = 0
2. 沒有作功 ΔW = 0
3. 因此 ΔU = 0 (故對理想氣體而言, ΔT = 0 )
4. 但若 ΔQ = 0 ,不正意味著 ΔS = ΔQ / T = 0 了嗎?
關鍵 : ΔQ 是否可逆循環
普遍來說,是 dQ ≤ T dS, ΔS = R ln 2
熵的統計基礎
除了自熱力學方式 dS = dQrev / T 定義熵之外,我們可透過統計來定義熵,想法如下:
第一定律 dU = TdS - p dV,也就是說(思考全微分)
T = (∂U / ∂S)V
或是等效地說
1/T = (∂S / ∂U)V
(為什麼上式是對的?)
現在,回顧 4.7 (我們在當時建構了理論溫度計的定義,它是基於平衡達成時,巨觀態機率的最大化演變,兩系統所會趨於一致的量,拿來訂作為"溫度"。而熱力學第零定律則配合之。)
1 / (kB T) = d ln Ω / d E
則得
S = kB ln Ω
(課文解釋)This is the expression for the entropy of a system which is in a particular
macrostate in terms of Ω, the number of microstates associated with
that macrostate.
(提醒:相空間的定義,不僅是微觀態數,且要是流動微觀態數)
我們在此是假設在該巨觀態的系統有固定的能量,這樣的情況又叫作 microcanonical ensemble。之後會再推廣到更複雜的狀況。
Ex 14.4 焦耳膨脹的熵變化(用相空間體積來看)
體積成兩倍後,每個分子可置的空間皆成兩倍:Ω = 2NA Ω0
S = kB ln Ω = kB ( ln 2NA + ln Ω0 ) = kB NA ln 2 + S0
ΔS = S - S0 = kB NA ln 2 = R ln 2
混合(過程)的熵
前言:一個非線性函數,如 f(x) = x2 ,f(2) + f(3) 與 f(2+3) 是不一樣的,差了交叉項 2 × 2 × 3。而熵 S(Ω)是 ln 函數, 其情況又如何?
考慮兩不同種之理性想氣體 ,各在 xV及 (1-x)V 容器中,有閥門連結,並讓兩邊的壓力 p 與溫度 T 相同。基於此,與理性想氣體方程式 p = (N/V) kB T , 則容器中分別有 xN 及 (1-x)N 氣體分子。如果閥門打開,則氣體會自發性混合。
gas 1 : xV -> V
gas 2 : (1-x)V -> V
理想氣體進行等溫膨脹其內能不變, 故其 T dS = p dV , 即
dS = p/T dV = N kB dV / V
ΔS = x kB ∫xVV (1/V1) dV1 + (1-x) kB ∫(1-x)VV (1/V2) dV2 = - N kB [ x ln x - (1-x) ln (1-x) ]
在 x = 0 及 x = 1 時, 無 混合故 entropy 改變, x = 1/2 時 改變達到最大, 為 ln 2,
ΔS 圖如下 :
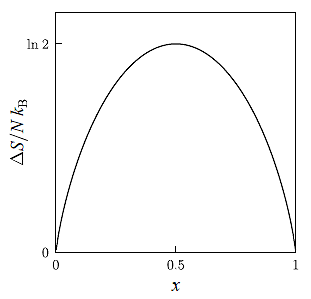
其中 x = 1/2 的情形極似先前 Joule Expansion 兩倍的討論, 故結果也是 ln 2
這裏的結果告訴我們一個重要的結論:"可區分性" 是極重要的觀念。
gas 1 與 gas 2 視為相同或不同,其結果完全不一樣。
誰決定兩個粒子可區分或不可區分?自然界或是觀察者?如何區分?
Ch.29 將回來繼續探討 "可區分性"
馬克斯威爾的精靈
馬克斯威爾的想像實驗,有一個精靈在觀看,看到快速分子,會打開閥問讓其進入特定區(如左側),如此一來,冷熱分離(違反常識/第二定律)。
早期的解釋,包含要精準測量時(例如光照)就會影響分子,所以不存在這種精靈的干擾,後來發現其實不然(可以設計出影響並不大的量測,畢竟這不是測不準原理適用的情境)。
事實上,此精靈基本上是一個可以貯存資訊的計算裝置。(詳見課本)
寫下資訊會減少熵,刪除資訊會增加熵(下一章會分析),讓整體總結果沒賺到。
討論:若不是計算裝置,而是自動化可重覆的程式(就沒有需要無限貯存空間的問題),如何?奈米機器人?速率選擇閥門 ?...。總是覺得精靈造得出來?那想一下,精靈存在 -> 冷熱分離 -> 溫差作功 -> 永動機誕生(會不管環境溫度多少,都持續提取系統溫度/內能拿去作功,直到絕對零度。)。 所以一開始就說了,精靈會導致第二定律的違反。有趣的是,上述各種可能的 精靈化身,要如何一一破解,說它們沒有能力違反第二定律?
熵與機率
前言:有時不知道微觀態的數目,僅知巨觀態的機率。我們希望
問題:如果有某些巨觀態在該次的測量是根本看不到,只看到其他巨觀態,怎麼辦?
問題:如果有一些巨觀量,它們之間的關係不是獨立的,怎麼辦?
(回到課文)
我們能夠量到的熵,當然是取決於系統可以存在的狀態總數(根據 S = kB ln Ω 公式),然而,每個狀態還可能是由多種不同且無法測量的微觀態所構成。因為系統存在於這些微觀態,這意味著額外的熵存在。見下例:
Ex 14.5 隱藏的微觀態,額外的熵
系統有 5 個均等機率的態,熵為 S = kB ln 5 。每個態若隱藏了三個微觀態,則系統實際上共有十五個微觀態,熵為 Stot = kB ln 15 = kB ln (3 × 5) = kB ln 3 + kB ln 5 = Smicro + S
S = Stot - Smicro
無法量測到的微觀態,對應到額外的熵 Smicro。
(思考:如果不是每個態後面都隱藏了一樣多的微觀態,怎麼辦?)若非如此,巨觀態就不會以現有的比例出現。
系統能處在(量不到的)微觀態的熵,為
Smicro = < Si > = Σi Pi Si
其中 Si = kB ln ni ,是巨觀態在 i 時,所有微觀態所構成的,i 態下的熵
重申此處 Pi 是某特定巨觀態被佔據的機率 , Pi = ni / N
(所謂隱藏的熵,是指 N 與 ni 實際的數值我們不知道。)
(問題:為什麼熵這個量在這裏要取這種期望值?是什麼時候規定了這個遊戲規則的?)
為什麼這樣做是對的?若事實上不是 N 與 ni ,而是乘上某個係數的 a N 與 a ni ,則 P'i = (a ni) / (a N) = ni / N = Pi 也仍會維持一樣,而各 S'i = kB ln (a ni) 則多了 kB ln a ,即 S'i = Si + kB ln a。此時 S'micro = < S'i > = Σi Pi S'i = Σi Pi ( Si + kB ln a) = Smicro + kB ln a ,只是多了常數,因此不知道隱藏熵多少,將不影響所有以下的討論。
基本觀念:熵是加的,機率是乘的。
熵是物理量,當然也可以透過 "平均" 這樣的觀念來處理。這個觀念,深植在可觀(物理)量是多次的統計平均之中。
相空間其流動性的意義一定要特別強調,(相空間就是相點掃過的範圍,相點不斷的在變動置,也就是說微觀態變化是不會停的),因此要用平均。
討論:為什麼 "隱藏熵" 會滿足 Smicro = < Si > = Σi Pi Si 這樣的定義?而總熵就不需要使用像這樣的公式?
對於隱藏熵的處理,我們是希望有利用前面已建立的熵公式,同時又能反映出沒表現在巨觀態(或沒能被測量到)的特性。
對同屬某 i 巨觀態的各不可測微觀態而言,假設其態數是 ni,該 i 態下熵是 ln ni,微觀態總數是 Σi ni = N,則
Stot = ln (Σi ni)
這和
Σi (ln ni)
並不一樣
按定義 每組 ni 自已有(量不到的)熵 Si = ln ni
系綜要表現出此一熵的總效應,則就必須透過 Si 的平均了,這是最直接的定義,所幸各 i 巨觀態出現的機率是很明確可被量到的,即 ni / N = ni / (Σi ni) 。
我們已經準備好要寫下可測熵之公式了,如下:
(我們將定位隱藏熵就是是總熵與可量測熵之間的差)
能被測量到的熵,S,為
S = Stot - Smicro
= kB ( ln N - Σi Pi ln ni )
= kB Σi Pi ( ln N - ln ni )
= kB Σi Pi ln (N / ni)
= - kB Σi Pi ln Pi
故有
S = - kB Σi Pi ln Pi
上式為 Gibbs 的熵表示法
(注意這裏的負號)
以下是兩個重要的例子:
Ex 14.6 每個巨觀態出現機率皆相等的例子
Ex 14.7 與波玆曼分佈的關係
熵既為 S = - kB Σi Pi ln Pi ,現在求怎樣的 {Pi} 會使 S 最大化?其中 {Pi} 是在 Σi Pi = 1 以及 Σi Pi Ei = U 的約制(前提)條件之下。
使用 Lagrange 未定乘子法(約制條件之下找極值的標準動作。)
竟可得到波玆曼分佈。