資訊理論
在本章我們將探討資訊的觀念以及其與熱力學熵的關係。乍聽好像很瘋狂,物理現象服從物理定律,而資訊就像是我們腦中可以理解的想法。(資訊也要遵守物理定律的話,那自由意志這個回事是不是根本不存在?)
套句作者講的話,"熱機與位元資料能有什麼共同點?" 事實上還蠻有關係的。為了對這件事有進一步的了解,以下先介紹一種熵的定義。
資訊 與 夏儂熵 (Shannon Entropy)
考慮以下三個皆為正確的陳述:
(1) 牛頓的生日是落在一年的某一天。
(2) 牛頓的生日是落在後半年。
(3) 牛頓的生日是落在某個月的 25 號。
第一句等於沒說,第二句資訊較多,第三句資訊更多。第二、三句匯集還能而產生更精確的結果。
問題是,"如何把資訊內容量化?"
一個我們無法不注意到的特性是,在沒有進一步更多資料的情況下,一個陳述裏的資訊越少,此陳述為真的機率越高。陳述 (1) 為真之機率 P1 = 1, 陳述 (2) 為真之機率 P2 = 1/2, 陳述 (3) 為真之機率 P3 = 12 / 365。再者,有效資訊 (2) 與 (3) 是獨立的,它們同時正確的機率自然是 P2 × P3 = 6 / 365。
(反對論者:但物理現象世界沒有邏輯上的真或偽,以真假來訂資訊量真的有物理上的意義嗎?"天空非常希臘" 這句詩又有多大的機率為真?)
獨立事件的機率是相乘,而資訊內容則是加成性的。我們因此可以想像一種類似熵的量,被定義來代表資訊(或資訊不確定性)的多寡,就是下面要介紹的夏儂熵:
一個陳述的 "資訊內容" Q 被定為
Q = - k log P
其中 P 是 "陳述的機率" 、k 為一正常數(須定為正乃因為我們希望 P 升高時,Q 會減少)。 若 k 定為 1、對數取 2 為底,我們是在表示 bit (位元)的資訊內容。 若定 k = kB,並以自然指數 e 為底, 我們在後面將會見到這與熱力學得到的熵一致。 在此先採用前者資訊觀點,對此,我們若有一組多個陳述,其機率為 Pi,其各自資訊內容 Qi = - k log Pi ,則其 "平均" 的資訊內容為
S = < Q > = Σi Qi Pi = - k Σi Pi log Pi
此一 平均 的 資訊內容 叫做 夏儂熵。
Ex. 15.1 一個公平骰子,每次投出結果的夏儂熵
Q = - k log 1/6 = k log 6、S = k log 6
取 k = 1 與對數基底 2, 夏儂熵值為 2.58 bits (注意單位)。
一個不公平骰子,假設投出點數 1, 2, 3, 4, 5, 6 之機率分別是 1/10, 1/10, 1/10, 1/10, 1/10, 1/2。則每種點數的資訊內容分別為 k log 10 (投出1~5)及 k log 2(投出 6),其平均資訊內容(即夏儂熵)為 k log √(20) ,即 2.16 bits 。
一個公平骰子的夏儂熵比不公平者大。
夏儂熵 量化了當我們測量某一個特定量,平均而言,我們獲得到多少資訊。另一種看法是:夏儂熵 量化了我們要測量的那一個量的不確定性(請參讀課本原文)。
(思考:重覆多次測量會不會改變夏儂熵?)
針對只有兩種結果的隨機過程(如丟銅板或明天是否下雨),以下再看具體的例子:
Ex 15.2 一個結果機率 P 及 1 - P 的 伯努力嘗試 (Bernoulli trial) 之夏儂熵是多少?
S = - Σi Pi log Pi = - P log P - (1 - P) log (1 - P)
,在此取了 k = 1 。不同 P 值的結果如下圖。P = 1/2 時熵最大,代表最大的不確定性。
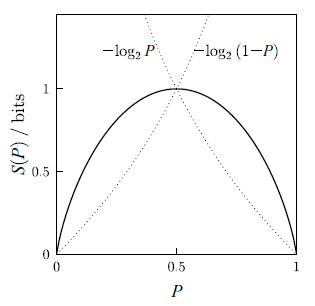
上圖中虛線呈現出個別態的 "資訊 (information)"。對結果機率為 P 者,資訊 Q1 = - log2 P 隨 P 遞減。當此一結果不太可能發生時(即 P 很小時), 得到該結果所對應到的資訊量就會非常大。最大平均資訊是發生在 P = 1 - P = 1/2,此時這兩種結果各有 1 位元的資訊對應到。
(從這個例子我們就體會到為什麼 要設 k = 1,並用 2 為底的 log。因為這樣一訂下來所造成的單位,巧妙地把變數對應到像是能在 0 與 1 兩個值變化的位元,符合我們對機率各半的位元其一種狀態時所帶有之資訊多寡的預期,即一位元的資訊量,即一位元的熵。位元所攜帶訊息多少的推斷。)
(為什麼商用數學裏面有機率統計,而比較沒有聽到有用到夏儂熵?)
(思考:夏儂熵是不是相當於富利葉或拉普拉斯那種一對一的轉換。只是讓問題的求解更容易?為回答這個問題,我們要看有什麼樣的物理定律或數學定理是跟夏儂熵有關。)
資訊與熱力學
雖說共通之處,在使用機率。但仍可有更深刻的關聯。
(詳見課本介紹說明)
夏儂熵的形式與 Gibbs 熵公式完全一樣,提供了 "熱力學熵究竟為何物" 的另一種看法,即對物性掌握之資訊不足以及並不在意系統具體是處於那個微觀態的情況下,我們對系統之 "不確性程度" 的度量。
這就是我們在前章 Ex 14.7 所做的:在能量 E 要固定的情況下,去極大化 Gibbs 熵,像變魔術一樣,就得到波玆曼分佈了。
然而,不僅資訊理論可以用在物理上這個層次,Landauer 進一步指出,資訊本身就是一個物理量。想像一個實體的計算裝置,貯存 N 位元資訊,並接到熱庫 T。
想永久自系統抹除此筆資訊,可將所有位元設 0 或全設為 1 ,(設到 0 與 1 一樣多可以嗎?亂設一通算不算抹除資訊?不然萬一原本要被抹除的資訊就是零怎麼辦?)。(也可想成,僅針對該資料區升高溫度, 使位元不穩定(消磁)) 此一過程必須是不可逆的。此一不可逆過程讓系統可能狀態少了 ln 2N (複習:可能性多了 2N 倍),故(熱力學)熵少了 N kB ln 2,或說少了每位元 kB ln 2。宇宙總熵不變的情況下,環境的熵就必須昇高每位元 kB ln 2,而環境溫度是 T,因此(也就是說)(這意味著釋放每位元 T dS = kB T ln 2 的熱到環境中,資訊因此是一個物理量。
(思考:可逆的熱才是熵,不可逆的熱還要多一點?)
問題:資訊是物理量嗎?壓縮過的資訊是物理量嗎?加密過的資訊是物理量嗎?部分遺失的不完整的資訊是物理量嗎?以上的這些,是同一個量嗎?其大小相同嗎?
老問題:一疊撲克牌有資訊內容嗎?一疊撲克牌的資訊是物理量嗎?
我們在這裏看到的是,資訊(組態)想要成為物理量,溫度(熱)的作用一定要考慮進來。這樣就又回到了原來的問題,一疊撲克牌的溫度是多少?
在(熱力)可逆的過程裏,時間沒有方向。這似乎也可看作是一種時間的不同步調,有別於相對論裏面的同時性不存在的現象。
資料壓縮
資料碼往往不是最精簡的,例如英語字首為 q 字母者後面常跟者 u 字母(翻字典看看)。另外,每個符號出現在語言中的比例不一樣,這也成為破解密碼的一種依據。資料壓縮是資訊理論的應用。(補充:ECC)
只介紹而不證明,夏儂的 無雜訊通道編碼定理 (Shannon's noiseless channel coding theorem) ,先看下例
Ex 15.3 試想以下的編碼:
00 -> 0
10 -> 10
01 -> 110
11 -> 1110
雖然看起來沒精簡到,但當 0 出現的機率比 1 出現的機率還要高的時候,其資料壓縮就顯著了。
上例給了我們一個 "如何用更一般性作法壓縮資料" 的線索,
從資料中找出典型序列(可多可少)
只針對典型序列加以有效編碼
假設對大量資料我們切分每 n 個位元一段, 則某特定 字串 x1, x2, x3, ..., xn 出現的機率
這是二項式分佈的某一個項的結構,其中位元 1 與位元 0,出現的機率分別是 P 與 (1 - P),因此位元 1 出現的個數約為 n P 個,位元 0 出現的個數約為 n (1 -P) 個,故某特定 n 字元 二進位字串出現的機率為
P(x1, x2, x3, ..., xn) = P(x1)P(x2)P(x3) ... P(xn) ~ PnP (1 - P)n(1 - P)
兩邊取 2 為底對數後
- log2 P(x1, x2, x3, ..., xn) ~ -n P log2 P - n (1 - P) log2 (1 - P) = n S
其中 S 就是之前得到過的 Bernoulli trial 的熵,上式等同如下:
P(x1, x2, x3, ..., xn) ~ 1 / 2nS
這意味著總數 nS 或(某個 R > S 的整數 R 的)nR 字串長度,就可以變化出 2nS 種不同序列 。(像是三爻合成一卦,可有八種卦狀態,六爻就六十四卦了),因而存在一個可靠的 (課本用 reliable 這個字) 編碼法;反之,使用的 R < S 的話,則任何編碼法皆不可靠(這裏的可靠是什麼意思?)也就是說,熵 S 最終決定了一筆資料壓縮率的極限。
量子資訊
資訊的概念也可以用在量子系統,而給出與我們熟悉的量子力學之結果。
前已見古典系統中資訊連結到機率,而量子系統裏機率則由密度矩陣 (density matrix) 取代,其基本特性的整理見課本 box 內的說明(有興趣者見之)。
對量子系統而言,資訊由算子
- k log ρ
所代表,其中ρ是 密度矩陣;在此我們也取 k = 1。 (思考:取不同 k 值的意義何在?) 如此,則平均資訊,即熵,就是 < - log ρ>,這催生了 范 諾伊曼 (von Neumann) 熵的定義
S(ρ) = - Tr (ρlog ρ)
若ρ的本徵值是 λ1, λ2, λ3, (註:密度矩陣的本徵值又叫做佔據數 occupation number)則
S(ρ) = - Σi λi log λi
這看來就很像是 Shannon 熵了。
Ex 15.4 (1) 證明純態的熵是零。(2) 如何才能使這個熵最大化?
(1) 利用基本性質 log 1 = 0。 (2) 每個態佔據一樣多。
不同於古典系統的 0 與 1,相當於涇渭分明的 yes 或 no,量子的二階系統的自由度是以 qbit(s) 來表示,它可以是兩個不同態 | 0 > 與 | 1 > 的線性組合。
課文中提及之進階議題:
Quantum entanglement 量子糾纏:兩個物體的態,可以是 | 01> + | 10 > / √2 的形式。
不可複製 (no-cloning) 定理:不可能複製一個非正交的量子態。
條件機率 與 聯合機率
條件機率 P(A | B) 是指 B 成立(B 事件發生)的情況下,A 成立(A 事件發生) 的機率。
聯合機率 P( A∩B ) 則是指 A、B 同時成立(A、B 兩事件皆發生)的機率。
很直觀可以理解:
P( A∩B ) = P(A | B) P(B)
P( A∩B ) = P(B | A) P(A)
若 A、B 為獨立事件,則 P(A | B) = P(A)(想想為什麼?),上式變成如預期之 P( A∩B ) = P(A) P(B)
考慮互斥事件 Ai,有 Σi P(Ai) = 1
我們因此可將某一事件的 X 的機率寫成
P(X) = Σi P(X | Ai) P(Ai)
以上諸條件,對下一節的證明有用。
貝氏定理
通常,知道假設(說) H 再來算結果 O 的機率 P(O | H) 是好算的,然而,也會需要知道 "在某結果 O 的情況下,來自假設 H 成立的機率是多少",即 P(H | O)。利用 P(O | H) 來算 P(H | O),可用所謂的貝氏定理如下:
P(A | B) = P(B | A) P(A) / P(B)
其中 P(A) 叫 prior probability (先驗概率/事前機率) ,P(A| B) 叫 posterior probability (事後機率),讀作 probability of A given B。
Ex 15.5 已知有一群運動員裏,百分之一有使用禁藥,藥檢的準確率是 95%。其中有一運動員被檢出陽性,問他有用禁藥嗎?
用藥行為的機率
P( 藥 ) = 0.01
P( 藥 ) = 0.99
用藥行為下,藥檢結果的條件機率
P( 陽 | 藥 ) = 0.95 (true positive)
P( 陽 | 藥 ) = 0.05 (false positive)
P( 陽 | 藥 ) = 0.95 (true negative)
P( 陽 | 藥 ) = 0.05 (false negative)
(註:這四式排下來,一路都是上一個與下一個的機率組合是 1,三個組合皆如此,想想看各基於什麼理由?)
我們會用到以下值,先算好
P( 陽 ) = P( 陽 | 藥 ) P( 藥 ) + P( 陽 | 藥 ) P( 藥 ) = 0.95 × 0.01 + 0.05 × 0.99 ~ 0.06
最終想知道的,是 "被驗出陽性者且是真的有犯規之機率",為
P( 藥 | 陽 ) = P( 陽 | 藥 ) P( 藥 ) / P( 陽 ) = (0.95) (0.01) / (0.06) ~ 0.16
這表示,藥檢陽性之此人,真有用藥的機率僅 16% !故不能藉此判定此人用禁藥。
這個例子的關鍵是,此一群選手中用藥率極低,因此有陽性藥檢結果出來的,大部分都是假陽性。 (那如何知道用藥率高低?還是要透過統計。)
Ex 15.6
崔利斯太太有兩個小孩,相差三歲,其中一個是男生。問她有女兒的機率為何?
若告訴你的是, "崔利斯太太有兩個小孩,高的那個是男孩",問她有女兒的機率為何?
(1) 按長幼排,男男、男女、女男。(女女必須排除)
(2) 高矮排:男男、男女
驚訝吧?機率取決於你知道的資訊。
在物理學裏,我們根據我們可以量到的量來推理這個世界。這樣的推理是基於機率與資訊理論,再把它套用到夏儂熵上。等 21 章我們學過了氣體粒子子的不可區分性之後,我們將會發現這裏頭真的是有熱力學上的涵意,而上面的例子則讓我們屆時不會訝異於那些結果。
再者,資訊理論實現了以部分之(不完整)情資來建構機率分佈而用以來研究系統的方法;即在某特定約制條件下極大化一個分佈的熵。這就是所謂的最大熵方法,它是對一組給定資料的基礎上所能做到之最無偏好的估計。熱力學就是最好的例子,波玆曼分佈即是得自在內能固定住的情況下,最大化 Gibbs 熵的結果。
