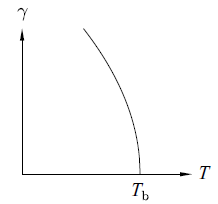桿子、泡泡,與磁鐵
到目前為止,第一定律寫成
dU = T dS - p dV
那是因為氣體以壓力作功,如果是其他形式的作功,可用
đW = X dx
流體、彈性桿、液體膜、(介)電性體、磁性物,各自對應的 intensive 與 extensive 量變數,見課本表,如下:。
| |
X |
x |
đW |
| 流體 |
-p |
V |
-p dV |
| 彈性棒 |
f |
L |
f dL |
| 液膜 |
γ |
A |
γ dA |
| 介電性 |
E |
pE |
pE · dE |
| 磁性 |
B |
m |
m · dB |
彈性桿
考慮一根桿子,截面積 A、長 L,在溫度 T 之下,受到微小張力 df 而造成微小長度變化 dL,我們定義楊氏模量為 應力應變的比,
應力 (stress) σ = df / A
應變 (strain) ε = dL / L
等溫楊氏模量 ET ≡ σ/ ε= L/A (∂f /∂L)T
ET 恆為正值(why ?) (有那種不拉還好,越拉越短的材質嗎?)
另有一對長桿狀物有用的量,即
線膨脹係數 (linear expasivity) αf = 1/L (∂L / ∂T )f
對大部份彈性體,αf 為正 (但橡膠則為負)
Ex 17.1 長度固定的金屬線,其張力如何隨溫度而改變?(有趣)
(∂f /∂T)L = - (∂f /∂L)T (∂L /∂T)f = -A ETαf
我們現在可以來看一看此一彈性系統的熱力學了
dU = T dS + f dL
則基於 F = U - T S ,有
dF = - S dT + f dL
則上式依全微分的定義是
S = - (∂F /∂T)L
f = (∂ f / ∂L)T
馬克斯威爾關係式為
(∂ S / ∂L)T = - (∂f /∂T)L
等號右邊是前面 Ex.17.1 的東西
(∂ S / ∂L)T = A ET αf
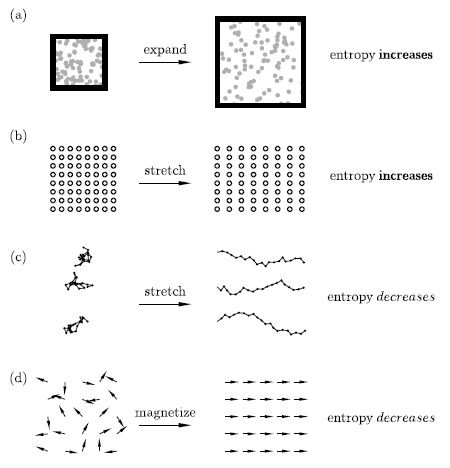
由上式可見,若線膨脹系數是正的,則拉長棒子會增加熵。這就像是理想氣體那樣,
(∂ S / ∂V)T = ( ∂p / ∂T)V > 0
因此每當有(定溫)體積膨脹時,熵是增加的。(我們在此還是對熵要怎麼增加有興趣)
為何拉長桿子會增加熵?以金屬為例,內有微晶構成故熵較低。拉長促使微晶形變令熵增加且吸熱。反之,以橡膠為例,拉長造成橡膠分子較規則排列,因而減少熵且放熱。。(見課本圖)
Ex 17.2 等溫膨脹時理想氣體的內能不變,等溫拉長時彈性桿的內能如何?
dU = T dS + f dL 再加上前面 (∂ S / ∂L)T = A ET αf 的結果,有
(∂U / ∂L)T = T (∂ S / ∂L)T + f = f + A T ET αf
這來自兩項的和,其中一項恆正的代表以功進入桿子;
另一項代表等溫下長度改變而流入桿子的熱。
對理想氣體而言,與上述分析情況一樣,只是作功與熱流這兩部分恰恰抵消。
表面張力
đW = γ dA
見下圖實驗裝置, đW = f ds = p dV
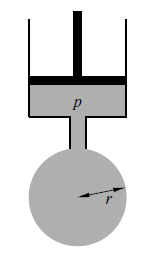
其中 dV = 4π r2 dr
又 dA = 4π(r + dr)2 - r2 ~ 8πr dr
đW = γ dA = 8πγr dr
將之等同上 p dV 的作功,有
8πγr dr = p (4π r2 dr)
得
p = 2γ/ r
Ex 17.3 半徑為 r 的(球狀)泡泡,其內部氣壓多少? (迷之音:這個也能估計?)
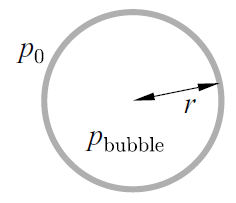
pbubble - p0 = 4γ/ r
表面張力的微觀解釋:構成液體之分子與鄰近分子的鍵結。
表面張力的另一種定義:從塊體切出一對表面所需要之每單位面積的能量。
含表面的熱力學第一定律(我們要從作功的討論進化到有溫度下的作功討論)
dU = T dS + γdA
亦有 dF = - S dT + γdA
想知道
(∂U/∂A)T = T (∂S/∂A)T + γ
由 dF 得 由 Maxwell 關係
(∂S/∂A)T = - (∂γ/∂T)A
故有
(∂U/∂A)T = T (∂S/∂A)T + γ = γ- T (∂γ/∂T)A
其中表面張力的溫度變化的驅勢如下(沸點後無表面張力可言)
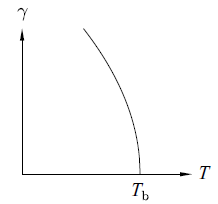
故 (∂γ/∂T)A 恆為負值,
這意味著有前式兩項貢獻(作功項跟熱流項)都是正的。
涉及到的熱是
ΔQ = T (∂S/∂A)T ΔA = T [- (∂γ/∂T)A]ΔA > 0
故為擴大表面積之動作導致吸熱(熵增加)。
思考:這裏的討論,一開始定下作功多少,純力學問題,that's fine。但後來熱力學條件是怎麼進來的?是到了那一步才成為熱力學問題的?
電性與磁性
假設我們想知道外加電場對系統的影響(作功)
d ( - E · pE ) = - pE · dE - E · dpE
在這裏比較麻煩的,是 dpE 本身會不會因 E 改變了而改變,要小心。
思考:d ( ) 裏面的 ( ) 當然是電位能, 但你能確定它是保守力作功嗎所 得到的嗎 ? (提示:如果把電偶極想成固定)
彈簧模型,補上
+ E · dpE
變成只剩下
đW = - pE · dE
課本說這樣的推論,可獲得磁性的版本如下:
đW = - m · dB
(其實要的就是上述的近似式)
註:外加電場或磁場所誘發的電偶極 pE 及磁矩 m 比較複雜,上列作功的貢獻是基於簡化的推論而得到的方便結果,僅代表主要的近似。較精確的計算必須還要考慮量子力學,並用數值方法進行所謂的第一原理計算。
順磁性
dU = T dS + B dm
(上式在教科書第二版已改為 dU = T dS - m dB) (第一版頁面 pdf)
m = M/V
,M 是磁化率、H 是磁場強度
χ = limH->0 M/H
對大部分順磁性材料而言,χ<< 1,即 M << H,而有 B = μ0 (H + M) ~ μ0 H ,因此
χ~ μ0 M / B
(上式等一下會用到)
χ 與溫度的關係, 有 Curie's law 描述,如下圖:
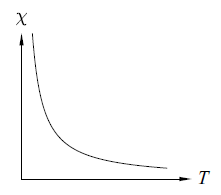
故 (∂χ/∂T)B < 0
下面會用到。
Ex 17.4 等溫磁化與絕熱去磁
把 - m B 加入 Helmhortz function F 中 (為什麼可以這麼做?) (第一版頁面 pdf)
F = U -T S - m B
(上式在教科書第二版已改為 F = U -T S )
(以下兩版相同)
dF = S dT - m dB
等溫磁化
(∂S/∂B)T = (∂m/∂T)B ~ VB/μ0 (∂χ/∂T)B
上式把定溫下的磁致熵變化,連結到磁納係數隨溫度的變化。
等溫之磁化所引起的熱流,為
ΔQ = T (∂S/∂B)T ΔB = TVB/μ0 (∂χ/∂T)B ΔB < 0
這是一個放熱過程。
絕熱下改變磁場所引起的 溫度變化,先寫下
(∂T/∂B)S = - (∂T/∂S)B (∂S/∂B)T
若我們定義固定磁場下的熱容是
CB = T (∂S/∂T)B
這是因為 ΔQ = CBΔT = T ΔS = T (∂S/∂T)B ΔT
此 1/ CB 連同 (∂S/∂B)T (即 VB/μ0 (∂χ/∂T)B )代入 (∂T/∂B)S之兩項積,得
(∂T/∂B)S = [ (∂S/∂T)B ]-1 VB/μ0 (∂χ/∂T)B = - TVB/(μ0 CB) (∂χ/∂T)B > 0
故增磁會增溫,因此降磁也就降溫,即(可逆)絕熱去磁過程會降溫。(用到了 (∂χ/∂T)B < 0 )
這種在固定熵之下來去磁的降溫方法,可達 mili-K (電子磁矩系統)甚至 micro-K (原子核磁矩系統)
等溫磁化與絕熱去磁的微觀圖像如下:
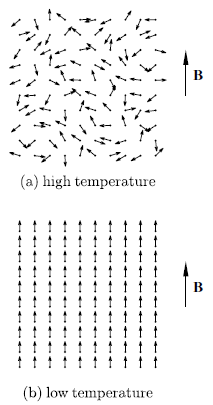
課本用磁組態的數目來求出熵,突顯其不同 T 、B 下的不同。
磁場變化循環之降溫方法:結合 等溫磁化 與 絕熱去磁
接上熱庫,等溫加磁場,把熱逼出散掉;移出熱庫,緩慢消磁,讓系統餘熱分到磁矩自由度上(使更紊亂),造或溫度下降。
量子能階圖像的解釋觀點:
(a) 原平衡態
(b) 等溫磁化
(c) 絕熱去磁
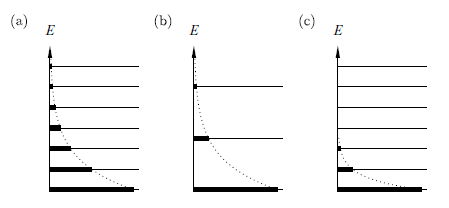
氣體、彈性桿、橡膠、磁矩系統之熵變化的總整理