當 T → 0,熱容趨於零
C = T (∂S/∂T) = (∂S/∂lnT) → 0
這是因為 T → 0 即、 ln T → - ∞ , 且 S → 0。只要 S → 某常數, ∂S 便 → 0。
回憶先前曾推導,每莫耳每個自由度是 C = R/2
熱膨脹停止
基於 T → 0 時 S → 0,(∂S/∂p)T → 0 當 T → 0(因為 "S→某常數" 意味著 ΔS → 0 )。利用 Maxwell 關係式(dU = T dS - p dV),有
1/V (∂V/∂T)p → 0,因此體膨脹係數 βp → 0。
T → 0 時任何氣體不再是理想
(單原子)理想氣體的特徵是 Cp - CV = R ,然而,當 T → 0 時, Cp 、 CV 皆為零,故前式不再成立。
另外,理想氣體 CV = 3/2 R ,故此式在 T → 0 時也不成立。
再者,前有 S = CV ln T + R ln V + constant ,一旦 T → 0 ,就會導致 S → - ∞ (違反第三定律)
越是低溫,微弱的交互作用越是重要。
居禮定律不成立
居禮定律陳述 χ∝ 1/T(即 χ正比於 1/T),故 T → 0 會導致 χ→ ∞,這樣不行嗎?
不行。第三定律意味著 (∂S/∂B)T → 0 (因為 S → 常數的話,ΔS → 0),而
(∂S/∂B)T = (∂m/∂T)B = VB/μ0 (∂χ/∂T)B ,故 (∂χ/∂T)B → 0,如此違反居禮定律。
居禮定律是基於每一個磁矩的行為是完全獨立而推導出來(指微觀推導的版本),χ是描述微小外加磁場下所引發的微小磁矩變化。當磁矩間的交互作用不可忽略時,更小的外加磁場就可以使磁矩扭轉。
也就是說,高溫時,kBT 遠大於交互作用能,各微觀單元顯得獨立無關,在低溫下,各單元行為獨立的假設不再成立。
絕對零度永不可及
以有限的步驟,不可能冷卻至 T = 0。
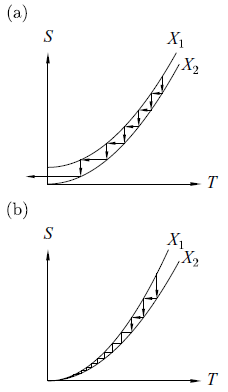
嚴密證明複雜,課本採下圖說明:
圖中 X1 及 X2 是參數(如磁場),降溫乃藉由等溫之下增加 X 與絕熱之下去除(減小) X 來達成。(圖中 X 的值是 X2 大於 X1) 。若降溫行為是 (a) 則有限步驟下絕對零度可達,若是 (b) 則不可達。為什麼 (b) 才是對的?因為第三定律的關係。
最後,一點關於卡諾引擎的討論:
卡諾引擎的效率是 eta = 1 - (TH / TL),若 TL = 0K,則效率為 1,即熱全轉功,違反第二定律。令人不禁想,有限次數達不到 0K 是否不需要使用第三定律作為條件?答案是,還是需要 第三定律,原因在於:想讓卡諾引擎其中一個熱庫是接在 0K 這樣的考量是有問題的,因為對於其中會經歷的等溫過程而言,一旦系統達到零度 K ,沒再把它加熱是改變不了其熱力學狀態的。<卡諾引擎接到 0K 熱庫,它就凍停了。> 一般因此認為第三定律是獨立於第二定律的假說。
第三定律替我們指出,一些簡單模型如理想氣體及居禮磁鐵,在絕對零度時的行為都要被修正。如此引發對物質之微觀熱性質作探討之動機,而開啟統計力學研究為下一個階段。