熱物理 期中考(2012 十一月)
10 題,每題 10 分
一、焦耳得以精準測量熱功當量的關鍵有那兩點?
1. 控制受熱液體與外界環境的溫差極小,使熱耗散減至最低。
2. 用長的溫度計使細刻度放大可辨,讀溫度數據精密讀取。
二、熱力學中的狀態函數為何(有那些)?其數學形式上要滿足什麼條件?
1. 壓力、體積、溫度、熵,皆是。
2. 必須為全微分形式者。 ∫AB dF = F(B) - F(A)
三、時間為什麼是有方向性的?
巨觀世界的變化中,涉及熱耗散者,其可能的過程極多,故雖每個微觀態過程皆是物理定律上的可逆,但總體巨觀變化要倒轉的機率極低。
四、導出理想氣體等溫過程中,熱流與體積的關係。
維持等溫,故
ΔT = 0
對理想氣體而言
dU = Cv dT
因此,一個等溫過程
ΔU = 0
這是因為其內能只與溫度有關,亦即
d U = 0
這表示,
dW = -dQ
則
ΔQ = -∫ dW = ∫V1V2 p dV = ∫V1V2 (RT / V) dV = RT ln V2/V1
五、導出理想氣體絕熱過程中,壓力與體積之間的關係。
(可逆) 絕熱膨脹有
d Q = 0
既然完全沒有熱流出入系統,我們轉而想知道,此一過程始末,該系統在各狀態函數上的差別
由於 d Q = 0,我們能用的條件是:
d U = d W
現在把等號兩邊與狀態函數的關係式寫出來,其中
d U = CV dT(理想氣體適用)
另有
dW = -pdV (可逆條件用上)
合併以上兩條件,我們因此有,對一莫耳的 (理想) 氣體
Cv dT = -p dV = -(RT / V) dV
移項
(1/T) dT = - R/CV (1/V) dV
積分得
ln T2/T1 = -R/CV ln V2/V1
此式可再進一步整理
利用 Cp = CV + R, 同除以 CV 得 γ = 1 + R / CV ,故 R / CV = γ- 1,即
ln T2/T1 = -(γ- 1) ln V2/V1
ln T2/T1 = ln (V2/V1)-(γ- 1)
T2 V2γ- 1 = T1 V1γ- 1
即
T Vγ-1 = 常數
或
p 1-γ Tγ = 常數
也就是
p Vγ = 常數
六、卡諾引擎為何?
由理想氣體的兩個等溫、兩個(可逆)絕熱過程,連接至高、低溫兩熱庫所構成(可逆)循環。
七、將理想氣體進行卡諾循環的熱流比 Qh / Ql ,以溫度比 Th / Tl 表示出來。
Qh / Ql = Th / Tl
八、引擎的效率如何定義?卡諾引擎的效率為何?
1. η ≡ W / Qh,其中 W 是作功, Qh 是 高溫熱流
2. ηC = 1 - Tl / Th
九、證明:所有連接兩個溫度(熱庫)之間運作的熱機,其 (引擎) 效率不會超過卡諾引擎者。
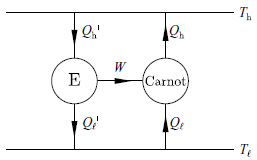
如果存在 E 比 Carnot engine 效率更高,即
ηE > ηCarnot
即
W / Q'h > W / Qh
因而
Qh > Q'h ,也就是說 Qh - Q'h > 0
另外,基於熱力學第一定律,
W = Q'h - Q'l = Qh - Ql
Qh - Q'h = Ql - Q'l
從上面 Qh - Q'h > 0 因此上式等號左邊為正,故等號右邊也是
但我們仔細看這個 Ql - Q'l 相當於自低溫熱庫 Tl 所抽走的熱量,如果它可以是正的,代表熱力學第二定律己經違反(故前面假設不可能成立)。
十、何謂克勞修司定理?
∫AB dQ/T ≤ 0 ,其中等號在過程為可逆時(即 dQ = dQrev) 成立。
