前已有
![]()
注意,(線性)變換係數是座標的函數,因此不同位置上向量的變動也不一樣。(回憶:Vμ 像是基底向量及梯度向量)
因此,d Aμ 不是一個張量,它涉及不同位置上向量的相減。我們可以直接 (依定義) 寫下 Aμ 的微分再變換座標看看(即上式對 x-barγ 一個微一個不微),結果為
![]()
上式 ∂Aμ /∂xβ 果然不是張量
回憶
![]()
組合偏微分與Γ,以下可看出滿足張量之形式
![]()
因此,定義符合張量
![]()
(問題:符合有什麼好?不符合又怎樣?)
(卡氏座標下,Christoffel 符號為零,故協變微分完全同義於一般微分)
(補充)幾何詮釋:向量如何平移?
協變導數是一個張量
![]()
反協變導數也可定義
![]()
對任何張量取協變導數,規則如下:
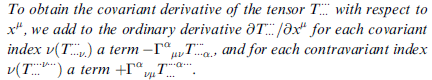
例如:
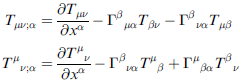
metric tensor gij 及 Kronnecker delta δij 的協變微分恆為零(見課本習題 1.38 )。