溫度的定義
溫度是冷熱程度的度量,它(與長度、質量、時間一般)是基本物理量
操作定義,溫度計(熱脹冷縮,水銀。酒精溫度計)
制(製)定溫度計
水的三相點
純物質的固、液、氣三相共存之特定的溫度與壓力,稱為三相點。(這是一個可靠而可作為準則的熱力學現象)
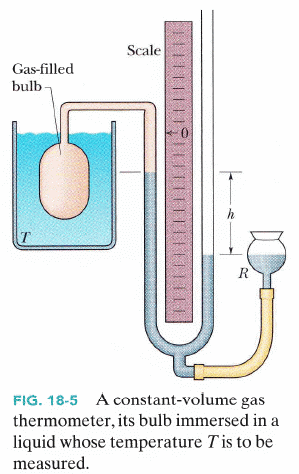
定容氣體溫度計
為冷熱的不同程度定刻度,是其他種類溫度計設定刻度的標準。用法:開口容器 R 的高度可調,永遠可使氣體與液面高度切齊尺上零刻度的位置,以確保氣體體積固定,並且在這樣的狀況下量到不同溫度時水銀柱的高度差。
其他種量測溫度的方式,紅外線量額溫、量耳溫;數位式溫度計(半導體在不同溫度下的導電方式
溫度相關的現象
溫度達到平衡的方式,冷觸熱 -> 升溫 +降 溫 -> 同溫
熱膨脹
熱脹冷縮是物質在不同溫度下的一個重要現象,參考教科書中舉了很多例子(其中鐵軌、溫控、假牙、噴射機身等)。
線膨脹
ΔL = L α ΔT
其中 α 是線膨脹係數,幾種表見參考書,注意冰的很大。
體膨脹
ΔV= V β ΔT
β= 3 α
作業:證明 β= 3 α
原因:ΔV = Vnew -V = (L+ΔL)3 - L3 =[ L(1+αΔT) ]3 - L3 ≈ 3 α L3 ΔT = βL3 ΔT = βVΔT
溫度與熱量
從溫度平衡的方式,人類發現熱(能量)從高溫流向低溫,直到兩者平衡為止。
高溫是因為物質儲較存了多熱量的關係
熱的定義:
熱是當系統與環境溫度不同時所移動的能量
熱容量 (Heat Capacity)
物體升高一度所需之熱量
Q = C ΔT = C (Tf - Ti)
石頭鍋要加熱很久才升溫,故不適合炒菜用,但石鍋一旦熱好可儲熱很久。(例:storage heater、岩燒牛排)
比熱 (Specific Heat)
單位質量的熱容
莫耳比熱
每莫耳的熱容
定容比熱 Cv 與 定壓比熱 Cp 的不同
即便之改變一度,系統也有可能對外作功。以氣體而言,固定體積下升溫一度與固定壓力下升溫一度所需之熱量可以有不小的差距。
熱力學第零定律
定義熱平衡:使用任何可受溫度影響指示或讀數的裝置,的
A ~ B 且 B ~ C,則 A ~ C (其中 "~" 代表熱平衡)