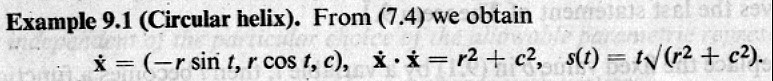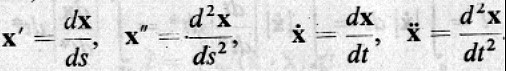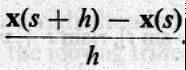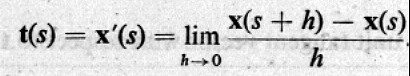希臘的幾何成就
畢達哥拉斯定理:
問題:何謂畢氏定理?(作業:如何定義直角)
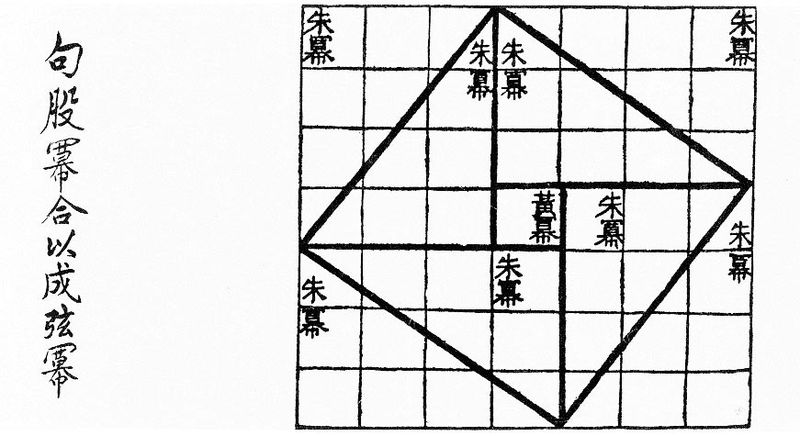
古中國叫"勾股弦定理"
古書中甚至轉述大禹因此治水成功,換用現代的語言,是應用數學原理成就精密的大型工程。
證明的方法很多,(但在此不採用三角函數的正餘弦定理 sin2θ + cos2θ = 1,這是因為這個三角函數的定理本身就是由畢氏定理證明出來的),以下介紹一個比之圖像化的證明。
(圖片出處:維基百科)http://zh.wikipedia.org/zh-tw/勾股定理
我們怎樣看畢氏定理?
多維度空間中長度的本質。即,長度與其投影在低維度裏的長度,它們之間有一定的關係。
誰不需要畢氏定理?
生存在一維空間中之智慧形式。
歐基里德:公設與證明
古希臘數學家歐幾里得的《幾何原本》提出了五條公設。頭四條公設分別為:
- 由任意一點到任意一點可作直線。
- 一條有限直線可以繼續延長。
- 以任意點為心及任意的距離可以畫圓。
- 凡直角都相等。
第五條公設說:同一平面內一條直線和另外兩條直線相交,若在某一側的兩個內角的和小於兩直角,則這兩直線經無限延長後在這一側相交。
是直尺與圓規的幾何
提前思考
平行線永不相交,問題在 什麼是「永不」嗎?還是 何謂「平行線」?
兩平行線最近距離可求,延伸 L 後,距離不變,將 L 趨近無窮。兩條直線,方向相同,謂之平行。
關鍵在什麼是「直線」?
(1)不彎,謂之直
(2)與線外參考點時時滿足勾股弦關係球面上如何定義直線?
思考:三角形的內角和為 180 度,四角形...、五角形...,有規則可循嗎?
奧依勒的多面體公式
v - e + f = 2
其中 v、f、e 各代表 "頂點 (vertex)"、"面 (face)"、"邊 (edge)" 的數目。
http://140.128.93.186/~chents/MG11
如何理解
雕刻家的觀點
思考三角錐頂點、四角錐頂點、. . . n 角錐頂點,在截去一角 ( v' = v - 1 + n ) 來增加了一個面 ( f' = f + 1) 時的結果:同時也增加了 n 個邊 ( e' = e + n )
(值得注意的是,上述截角的動作是可 逆的。 )
可見 v' - e' + f' = v - e + f 會是常數
剩下的問題是,這個常數值是多少
考慮最簡單的四面體錐
1 + n = (n - 1) + ?
可見這個 "?" 是 2
一次截去兩個頂角可以嗎?試試看
一次切掉兩個頂點的情形
分析:假設切面與多面體相交的新斷面有 n 個頂點,
頂點:v' = v + n - 2 (產生了 n 個新頂點,但原本有兩個頂點被截掉了)
邊:e' = e + n - 1 (環狀 n 頂點圍出 n 個邊,但原截角兩個頂點間有一個邊少掉了)
面: f' = f + 1 (截角的動作,並未讓原面體的面有減少,反倒是多了一個截面)
如此,仍舊一樣是 v' - e' + f' = v - e + f
(其他的證明方式可見維基百科或科普書)
證明 : http://plus.maths.org/content/eulers-polyhedron-formula
補充:高維度公式
( http://www.math.osu.edu/~fiedorowicz.1/math655/HyperEuler.html )
Gauss-Bennet 定理
幾何與空間規律 (晶體與對稱性)