Euler Mehod
對於一個微小的步幅 (step) h 而言, 若從第 n 步要推到第 n+1 的方法是依以下的方式,就是前面已經提到過的奧依勒法:
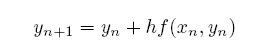
從圖像上來看,它是以第 n 點為立足點,在那裏求出切線方向出發(斜率函數是題目給的),利用該方向來走一步,到達第 n+1 點,如此一步一步地走下去,如下圖所示:
常微分程求解:隆巨—庫塔法、高階方法的圖像
演算法公式與其圖像表示
Euler Mehod
對於一個微小的步幅 (step) h 而言, 若從第 n 步要推到第 n+1 的方法是依以下的方式,就是前面已經提到過的奧依勒法:
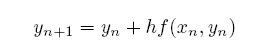
從圖像上來看,它是以第 n 點為立足點,在那裏求出切線方向出發(斜率函數是題目給的),利用該方向來走一步,到達第 n+1 點,如此一步一步地走下去,如下圖所示:
2nd Order Runge-Kutta Method
前面我給大家示範過,利用兩個半步與一個整步的組合,可以創造出精確度達到二階(即誤差從三階開始),但卻只要乘上微小量 h 一次的公式的公式,其中必須付出的代價是,比起上面的 Euler 法要多算 k2(請注意到它是求值在半步的地方):
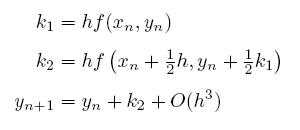
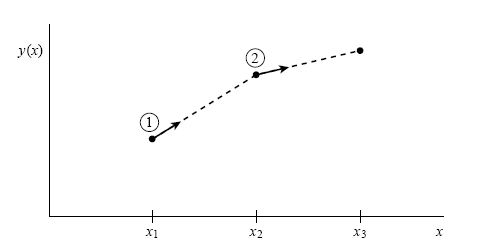
上面的公式從圖像上很容易可以看出其策略,在起點處所求得的斜率,先只走一半到中間點,在那裏再求一次斜率,然後退回到起點利用這個中點斜率走完整一步到下一步,如此得到 yn+1,就是圖上標為 (3) 的地方。這就是一個二階的 step,下一個 step 會落在標為 (5) 處,如此再一次一次走下去。 整個策略看起來,有進兩步、退一步,以退為進的感覺。
4th Order Runge-Kutta Method
最常用且通用的 RK 方法是四階的,我們可以想見它是由更多不同樣式的半步組合所構成,其中並包含了原有的起點處定斜率與終點處定斜率,請注意這裏 k1、k2、k3、k4 的定義與其相依性(即 k4 用到 k3、k3 用到 k2、k2 用到 k1 的狀況)
(事實上)這裏的圖是有印錯的情況,我認為 2 與 3 的標注處應該對調,公式中的 k1、k2、k3、k4 全部都有 h ,但分別是乘以 (a) 在起點處 1 求的斜率、(b) 以起點斜率走半步到 2 處求斜率、(c) 一樣從起點開始但,改採前面的半步處 2 之斜率,重走半步到 3 後求斜率,以及最後 (d) 採用上一個於 3 處所獲得的斜率,從起點出發走一整步到 4 處求斜率。
副程式及使用上的注意事項
副程式 rk4
注意事項及技巧:
rk4 進行一步的 4 階 R-K 計算, 值得注意的是宣告為 external 的 derivs,它是一個要由使用者提供的副程式,然而,為什麼在 rk4 的引數列裏面(最後一項)也出現有 derivs 的名稱呢?這有一個好處,就是使用者提供的副程式可以叫做別的名稱,比方說 derivs01,而 rk4 要呼叫它時,就寫成 call rk4(....,derivs01) 這樣,如此在 rk4 內部自已仍認為是在使用標準為稱的 derivs,和一般副程式傳變數的情況一樣。
副程式 rkdumb
注意事項及技巧:
rkdumb 是一個固定步幅的所謂 driver(驅動)程式,使用每次只走一步的單純的工具程式 (在這裏是 rk4)一直進行很多步,把整個解一步一步做出來。在這個副程式中,你要給自變數(上下限)範圍 x1、x2 以及共分割多少步 nstep,此 driver 程式會以等步幅求解原未知函數。"Dumb" 本身是 "笨"、"呆" 的意思,作者這樣叫是因為下一節會介紹較聰明的 driver 程式,它是可以做每個單一步幅大小的控制以達到最佳的計算效果(指同樣精密度的要求下以最少時間完成)。
在寫主程式來呼叫 rkdumb 時,首先注意 vstart 在 rkdumb 中宣告為陣列 vstart(n),但 n 的值在 rkdumb 中卻沒有設定(只有宣告它是整數),所幸它在引數列中是有傳進來,這就表示在編譯的時候仍可以透過繼承上層程式的屬性而具有明確的值(宣告陣列時陣列的大小必須明確設定,可執行檔才能知道要替那個變數保留多少記憶體空間大小)。因此,為了配合副程式中宣告了 vstart(n) 而只傳 n 進去,主程式在宣告 n 為整數後就還用 parameter (n=?) 這個指令將 n 值設定為某特定常數。
rkdumb 會把整個 x1 到 x2 間 nstep 那麼多點的 xn 值及 yn 值都保留下來,這整組數值計算結果就可以代表 y(x) 這個解(這個解是唯一存在的,詳細證明可參考相關數學書籍,如 Keryszig 的高等工程數學:第九版)。主程式的重要任務當然是從取得這些資料,並把它輸出或保存。rkdumb 用 common /path/ xx,y 的語法把 xx(NSTPMAX) 及 y(NMAX,NSTPMAX) 儲存在 path 這個可共享的公共區塊(common block)中,它的功能是讓其他上層或下層的副程式都不必傳引數也能用得到區塊裏面的資料,只要一開始也作相同的 common /path/ x1,y1 宣告即可,注意區塊名 path 要一樣,變數名稱則可以不同。
關於 common block 的進一步用法說明,可見 配合教科書的其他指令,或參見手冊: http://proton.phys.tku.edu.tw/pgi/doc/pgf77_ref/f77ref04.htm#Heading68
範例程式:
program rkdumb_main
implicit none
integer nstep,NMAX,NSTPMX,n_var,i,j,pgopen
parameter (NMAX=50,NSTPMX=200,n_var=2)
real xx(NSTPMX),y(NMAX,NSTPMX),x1,x2,vstart(n_var),yy(NSTPMX)
real y_min(NMAX), y_max(NMAX)
common /path/xx,y
external my_derivs
write(*,*) 'Type in initial and final values of x :'
read(*,*) x1,x2c Be careful the max value of nstep is 199, not 200, see rkdumb.
100 write(*,*) 'How many steps to integrate the solution ? (<= 199)'
read(*,*) nstep
if (nstep.gt.199) goto 100
if (nstep.lt.0) goto 100write(*,*) 'Your problem is an order- ',n_var,' ODE.'
do i=1,n_var
write(*,*) 'Give the initial value y',i,'(x0) :'
read (*,*) vstart(i)
end docall rkdumb(vstart,n_var,x1,x2,nstep,my_derivs)
write(*,*) 'RK routine has completed.'c Find Max and min values of yi(x), but here we will use only y1(x).
do i=1,n_var
y_max(i)= y(i,1)
y_min(i)= y(i,1)
end do
do i=1,n_var
do j=1,nstep
if (y(i,j).gt.y_max(i)) y_max(i)=y(i,j)
if (y(i,j).lt.y_min(i)) y_min(i)=y(i,j)
end do
end doc Copy y(1,1:nstep) to yy(1:nstep) for PGLINE plotting
do i=1,nstep
yy(i) = y(1,i)
end doc Start plotting
if (pgopen('/xwin').le.0) stop
call pgpap(6.0,0.75)
call pgenv (x1,x2,y_min(1),y_max(1),0,0)
call pgline(nstep,xx,yy)
call pgclosend
subroutine my_derivs(x,y,dydx)
real x,y(2),dydx(2)
dydx(1) = y(2)
dydx(2) = -y(1)
end注解:本例範的原給定微分方程題目,是求解 y''(x) + y(x) = 0 這樣的一個微分方程式。由於這是一個二階常微分方程式,因此必須轉化成兩條一階常微分方程式,其作法是,首先,依本單元之定義所待解未知函數 y 為 y1,並定義 dy1/dx = y2,這就所要之兩條一階微分方程式的第一條,另外,將 dy1/dx 按剛才的定義代入原微分方程式,得 dy2/dx = -y1,如此得到所要之兩條微分方程式的第二條。一併列出,呈 dy1/dx = y2 與 dy2/dx = -y1 聯立,因此在上例 my_derivs 副程式有 dydx(1) = y(2) 與 dydx(2) = -y(1) 這兩行指令。注意在一般的情形下,都會是與 x 有關的,不是像本例中之常微分程式那樣恰好與 x 無關。
補充閱讀: